Efecto Doppler


El efecto doppler (llamado así en honor al físico y matemático austriaco Christian Andreas Doppler) es el cambio de frecuencia aparente de una onda producido por el movimiento relativo de la fuente respecto a su observador.[1]
Hay ejemplos cotidianos del efecto doppler en los que la velocidad a la que se mueve el objeto que emite las ondas es comparable a la velocidad de propagación de esas ondas. La velocidad de una ambulancia (50 km/h) puede parecer insignificante respecto a la velocidad del sonido al nivel del mar (unos 1235 km/h), sin embargo, se trata de aproximadamente un 4 % de la velocidad del sonido, fracción suficientemente grande como para provocar que se aprecie claramente el cambio del sonido de la sirena desde un tono más agudo a uno más grave, justo en el momento en que el vehículo pasa al lado del observador.
En el caso del espectro visible de la radiación electromagnética, si el objeto se aleja, su luz se desplaza a longitudes de onda más largas, produciéndose un corrimiento hacia el rojo. Si el objeto se acerca, su luz presenta una longitud de onda más corta, desplazándose hacia el azul. Esta desviación hacia el rojo o el azul es muy leve incluso para velocidades elevadas, como las velocidades relativas entre estrellas o entre galaxias, y el ojo humano no puede captarlo, solamente medirlo indirectamente utilizando instrumentos de precisión como espectrómetros. Si el objeto emisor se moviera a fracciones significativas de la velocidad de la luz, sí sería apreciable de forma directa la variación de longitud de onda.
Descubrimiento[editar]
Doppler propuso este efecto en 1842 en su tratado Über das farbige Licht der Doppelsterne und einige andere Gestirne des Himmels (Sobre el color de la luz en estrellas binarias y otros astros).[2] El científico neerlandés Christoph Hendrik Diederik Buys Ballot investigó esta hipótesis en 1845 para el caso de ondas sonoras y confirmó que el tono de un sonido emitido por una fuente que se aproxima al observador es más agudo que si la fuente se aleja.[3] Hippolyte Fizeau descubrió independientemente el mismo fenómeno en el caso de ondas electromagnéticas en 1848. En Francia este efecto se conoce como «efecto Doppler-Fizeau»[4] y en los Países Bajos como «efecto Doppler-Gestirne». En Gran Bretaña, John Scott Russell hizo un estudio experimental del efecto doppler (1848).[5]
Generalidades[editar]
En física clásica, donde las velocidades del emisor (también denominado «fuente») y del receptor (o también «observador») con respecto al medio son inferiores a la velocidad de las ondas en el propio medio, la relación entre la frecuencia observada y la frecuencia emitida viene dada por:[6]
| Símbolo | Nombre |
|---|---|
| Frecuencia observada | |
| Frecuencia emitida | |
| Velocidad de las ondas en el medio | |
| Velocidad del receptor en relación con el medio; positiva si el receptor se está moviendo hacia el emisor (y negativa en el sentido opuesto) | |
| Velocidad de la fuente con respecto al medio; positiva si la fuente se aleja del receptor (y negativa en el sentido opuesto) |
(Conclusión: la frecuencia aumenta cuando fuente y observador se acercan entre sí, y se reduce cuando se alejan).
En la fórmula anterior se supone que la fuente está acercándose (o alejándose) «directamente» del observador. Si la fuente se acerca al observador con velocidad constante, pero en una trayectoria «no incidente» (como por ejemplo, un avión en vuelo respecto a un observador situado en tierra), entonces:
- La frecuencia que el observador escucha primero es más alta que la frecuencia emitida desde el objeto.
- A continuación se produce una disminución gradual de la frecuencia percibida a medida que la fuente se acerca al observador, coincidiendo la frecuencia percibida con la original cuando la onda llega desde una dirección perpendicular al movimiento relativo (es decir, cuando fue emitida desde el punto más cercano al observador, aunque cuando se reciba la onda, la fuente y el observador ya no estarán en su posición más próxima).
- Finalmente, el observador percibirá una continua disminución de la frecuencia a medida que se aleja la fuente.
Cuando el observador se encuentra muy cerca de la trayectoria del objeto, la transición de alta a baja frecuencia es muy abrupta. En cambio, cuando el observador está lejos de la trayectoria del objeto, la transición de alta a baja frecuencia es gradual.
Si las velocidades y son pequeñas en comparación con la velocidad de la onda, la relación entre la frecuencia observada y la frecuencia emitida es aproximadamente[6]
| Frecuencia observada | Cambio de frecuencia |
|---|---|
- donde
- es la velocidad del receptor respecto a la fuente: es positiva cuando la fuente y el receptor se acercan.
|
Dada dividiendo por
A partir de se puede deducir la expresión geométrica:
|
Situación estacionaria, subsónica, sónica y supersónica.[editar]
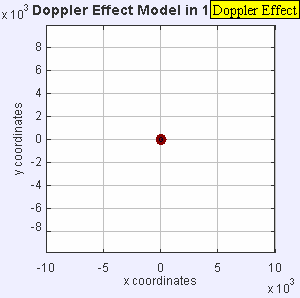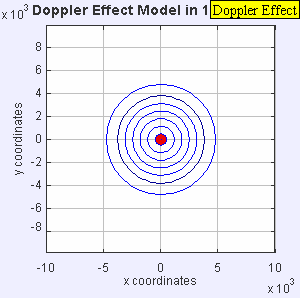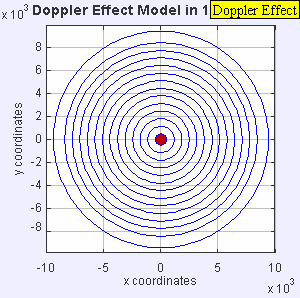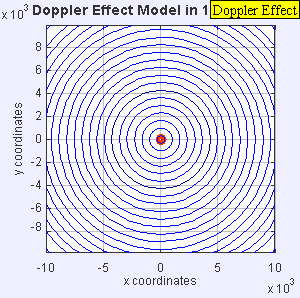
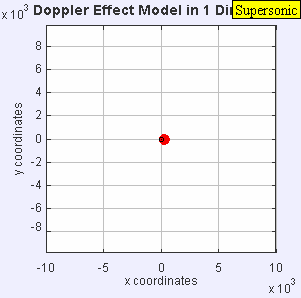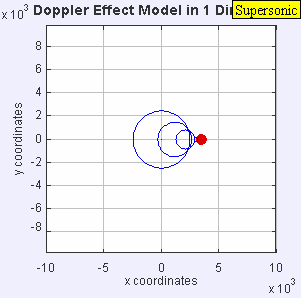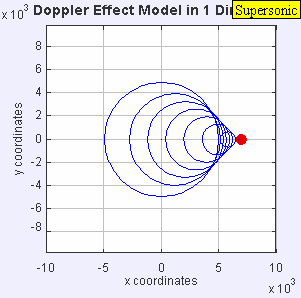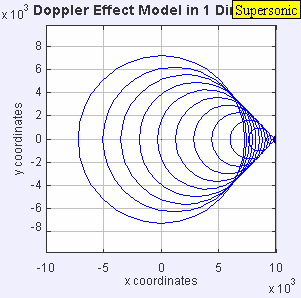
En los cuatro gráficos siguientes se incluye una animación con el análisis del comportamiento de las ondas sonoras en los cuatro casos característicos del efecto doppler en relación con la velocidad del emisor respecto a la velocidad de propagación del sonido en el aire (Mach 1):
- Comportamiento de las ondas sonoras
-
Una fuente de audio fija produce ondas de sonido a una frecuencia constante f, y los frentes de onda se propagan de forma simétrica alejándose de la fuente a una velocidad constante c. La distancia entre los frentes de onda es la longitud de onda. Todos los observadores escucharán la misma frecuencia, que será igual a la frecuencia real de la fuente donde f = f0
-
La misma fuente de sonido está irradiando ondas de sonido a una frecuencia constante en el mismo medio. Sin embargo, ahora la fuente de sonido se mueve con una velocidad de υs = 0.7 c (Mach 0,7). Puesto que la fuente está en movimiento, el centro de cada nuevo frente de onda está ligeramente desplazado a la derecha. Como resultado, los frentes de ondas comienzan a acumularse en el lado derecho (por delante) y quedan más distanciados en el lado izquierdo (detrás) de la fuente. Un observador frente a la fuente escuchará una frecuencia más alta:
-
Ahora la fuente se está moviendo a la velocidad del sonido en el medio (υs = c, (es decir, a Mach 1). Los frentes de onda enfrente de la fuente están ahora todos acumulados en el mismo punto. Como resultado, un observador enfrente de la fuente no detectará nada hasta que la fuente llegue a su posición
-
La fuente de sonido ya ha superado la velocidad del sonido en el medio, y se desplaza a 1,4 c (Mach 1.4). Puesto que la fuente se está moviendo más rápido que las ondas de sonido que crea, lo que realmente hace es dirigir el frente de ondas a medida que avanza. La fuente de sonido pasará ante un observador en reposo antes de que el observador oiga el sonido. Como resultado, un observador situado enfrente de la fuente percibirá: f = c + 0c - 1.4c f0 = -2.5 f0 y un observador detrás de la fuente escuchará una frecuencia más baja: f = c - 0c + 1.4c f0 = 0.42 f0 .
Análisis[editar]

Para entender lo que sucede, considérese la siguiente analogía. Alguien lanza una bola cada segundo a un hombre. Se asume que las bolas viajan con velocidad constante. Si el lanzador está parado, el hombre va a recibir una bola cada segundo. Sin embargo, si el lanzador se está moviendo hacia el hombre, este va a recibir las bolas con mayor frecuencia debido a que las bolas estarán menos espaciadas, ya que cada bola debe recorrer menos distancia que la anterior para llegar al receptor. El inverso es cierto si el lanzador se aleja del hombre. Por lo que en realidad es la longitud de onda la que es afectada; como consecuencia, la frecuencia recibida también se ve afectada. También puede afirmarse que la velocidad de la onda permanece constante, mientras que se producen cambios en la longitud de onda; y por lo tanto, la frecuencia cambia también.
Para un observador en reposo respecto al medio, si una fuente en movimiento está emitiendo ondas con una frecuencia real dada (en este caso, la longitud de onda cambia pero la velocidad de transmisión de la onda se mantiene constante, por lo que la velocidad de transmisión de la onda no depende de la velocidad de la fuente), entonces el observador detecta ondas con una frecuencia dada por:
Un análisis similar para un observador en movimiento y una fuente estacionaria (en este caso, la longitud de onda se mantiene constante, pero debido al movimiento, la velocidad a la que el observador recibe las ondas, y por lo tanto la velocidad de transmisión de la onda [con respecto al observador] cambia) produce la frecuencia observada:
Esto se puede generalizar en la ecuación que se presentó en la sección anterior:
Un efecto interesante fue predicho por lord Rayleigh en su libro clásico sobre el sonido: si la fuente se acerca al observador a dos veces la velocidad del sonido, una pieza musical emitida por dicha fuente se oiría en el tiempo y tono correcto, pero al revés (es decir, las notas del final de la pieza llegarían al observador antes que las de su comienzo).[7] El efecto doppler sobre el sonido solo se percibe claramente con objetos moviéndose a bastante velocidad: el cambio en la frecuencia de tono musical implica una velocidad de alrededor de 40 metros por segundo (144 km/h). Sin embargo, los cambios de amplitud de los sonidos de los emisores en movimiento pueden ser fácilmente confundidos con pequeños cambios en la frecuencia. Neil A. Downie ha demostrado[8] cómo el efecto doppler puede hacerse mucho más fácilmente audible mediante el uso de un emisor ultrasónico (por ejemplo, de 40 kHz) emitiendo desde objetos en movimiento. El observador debe utilizar un convertidor de frecuencia heterodino (como los que se utilizan en muchos detectores de murciélagos) con capacidad para trabajar en la banda de hasta los 40 kHz. En este caso, con el receptor ajustado para traducir las ondas recibidas a la banda de los 2000 Hz para hacerlas audibles, basta con que el emisor se desplace a tan solo 2 metros por segundo para que el observador perciba un desplazamiento de frecuencia de un tono entero (240 Hz).
- Trayectoria del emisor no incidente en el receptor
En el caso de la sirena de un vehículo de emergencia en movimiento que pasa cerca de un observador, comenzará a oírse con una frecuencia más alta que la de su tono estacionario. Irá bajando a medida que se acerque, y continuará reduciéndose (por debajo de su tono estacionario) a medida que se aleje del observador. El astrónomo John Dobson explicó el efecto de este modo:
- "La razón por la que se percibe cómo se desliza gradualmente el tono de la sirena es porque no arrolla al observador."
En otras palabras, si la sirena se acercase al observador directamente (con velocidad constante), la frecuencia percibida permanecería invariable hasta que el vehículo lo alcanzara, para saltar inmediatamente a un nuevo tono más bajo en cuanto empezara a alejarse. Debido a que el vehículo no pasa por el punto exacto que ocupa el observador, sino que lo rebasa a cierta distancia, su velocidad relativa presenta una componente radial que no permanece constante, sino que varía como una función del ángulo entre su línea de visión y la velocidad del vehículo que porta la sirena:
donde es el ángulo entre la velocidad de avance del objeto y la línea de visión desde el objeto hacia el observador.
Álgebra del efecto doppler en ondas sonoras[editar]
Observador acercándose a una fuente[editar]
Imagínese que un observador O se mueve con una velocidad que tiene una dirección y sentido hacia una fuente de sonido S que se encuentra en reposo.[9] El medio es aire y también se encuentra en reposo. La fuente emite un sonido de velocidad , frecuencia y longitud de onda . Por lo tanto, la velocidad de las ondas respecto del observador no será , sino la siguiente:
Sin embargo, como la velocidad del medio no cambia, la longitud de onda será la misma, por lo tanto, si:
Pero, como se menciona en la primera explicación, el observador al acercarse a la fuente oirá un sonido más agudo; esto implica que su frecuencia es mayor. A esta frecuencia mayor captada por el observador se la denomina frecuencia aparente, que se denomina.
El observador escuchará un sonido de mayor frecuencia debido a que
Observador alejándose de una fuente[editar]
Analícese el caso contrario: cuando el observador se aleja de la fuente, la velocidad será y de manera análoga se puede deducir que
Fuente acercándose al observador[editar]
En este caso la frecuencia aparente percibida por el observador será mayor que la frecuencia real emitida por la fuente, lo que genera que el observador perciba un sonido más agudo.
Por tanto, la longitud de onda percibida para una fuente que se mueve con una velocidad será:
Como se puede deducir que:
Fuente alejándose del observador[editar]
Haciendo un razonamiento análogo para el caso contrario: fuente alejándose; se puede concluir que la frecuencia percibida por un observador en reposo con una fuente en movimiento será:
Cuando la fuente se acerque al observador se pondrá un signo (−) en el denominador, y cuando la fuente se aleje se reemplazará por (+).
Al terminar de leer lo anteriormente expuesto surge la siguiente pregunta: ¿Qué pasará si la fuente y el observador se mueven al mismo tiempo?. En este caso particular se aplica la siguiente fórmula, que no es más que una combinación de las dos:
El sentido del desplazamiento de la fuente y el observador son inversos:
Si el observador se acerca a la fuente el numerador es positivo, si se aleja negativo.
Si la fuente de sonido se acerca al observador el denominador es negativo, si se aleja es positivo.
Se puede dar el caso de numerador y denominador sean una suma, y también de numerador y denominador sean una resta.
Ejemplo[editar]
Un observador se mueve a una velocidad de 42 m/s hacia un trompetista en reposo. El trompetista está tocando (emitiendo) la nota la (440 Hz). ¿Qué frecuencia percibirá el observador, sabiendo que = 340 m/s
Solución: Si el observador se acerca hacia la fuente, implica que la velocidad con que percibirá cada frente de onda será mayor, por lo tanto la frecuencia aparente será mayor a la real (en reposo). Para que esto ocurra se debe aplicar el signo (+) en la ecuación.
En este caso particular, el trompetista emite la nota la a 440 Hz; sin embargo, el observador percibe una nota que vibra a una frecuencia de 494,353 Hz, que se aproxima altamente a la frecuencia perteneciente a la nota si. Musicalmente hablando, el observador percibe el sonido con un tono más agudo del que se emite realmente.
Álgebra del efecto doppler en ondas electromagnéticas[editar]
En el caso de ondas electromagnéticas la fórmula de efecto doppler es: Siendo f la frecuencia del emisor, f' la que ve el receptor, v la velocidad del emisor respecto al receptor y el factor de Lorentz dado por:
|
Para analizar el caso de las ondas electromagnéticas se usaran las transformaciones de Lorentz para pasar del sistema de referencia emisor al receptor; siendo las magnitudes con prima las del receptor y las sin prima las del emisor. Se supondrá que la onda y el emisor se mueven hacia la derecha. Supóngase que el emisor está emitiendo una onda de la forma: Las transformaciones de coordenadas serán: Sustituyendo en la función de ondas y comparando con la función de onda en el sistema de referencia receptor: Se obtiene que: o en términos de las frecuencias: |
Aplicaciones[editar]
Astronomía[editar]

El efecto doppler sobre las ondas electromagnéticas como la luz es de gran utilidad en astronomía, y se manifiesta en los denominados corrimiento al rojo o corrimiento al azul. Se ha utilizado para medir la velocidad a la que estrellas y galaxias están acercándose o alejándose de la Tierra; es decir, sus velocidades radiales. Este fenómeno físico se utiliza para detectar estrellas binarias, para medir la velocidad de giro de las estrellas y galaxias, o para detectar exoplanetas. (Debe tenerse en cuenta que el desplazamiento al rojo también se utiliza para medir la expansión del espacio, aunque en este caso no se trata realmente de un efecto doppler).[10]
El uso del efecto doppler sobre la luz en astronomía depende del conocimiento que se tiene de que los espectros de las estrellas no son homogéneos. Exhiben líneas de absorción definidas de las frecuencias que están en correspondencia con las energías requeridas para excitar los electrones de varios elementos de un nivel a otro. El efecto doppler es reconocible en el hecho de que los patrones conocidos de las líneas de absorción no aparecen siempre coincidiendo con las frecuencias que se obtienen a partir del espectro de una fuente de luz estacionaria. Dado que la luz azul tiene una frecuencia más alta que la luz roja, las líneas espectrales de una fuente de luz astronómica que se acerca exhiben un corrimiento al azul, y las de uno que se aleja experimentan un corrimiento hacia el rojo.
Entre las estrellas más cercanas a la Tierra, las mayores velocidades radiales con respecto al Sol son +308 km/s (BD-15°4041, también conocida como LHS 52, situada a 81,7 años luz de distancia) y –260 km/s (Woolley 9722, también conocida como Wolf 1106 y LHS 64, situada a 78,2 años luz de distancia). Una velocidad radial positiva significa que la estrella se está alejando del Sol, negativa que se está acercando.
Radar[editar]
El efecto doppler se utiliza en algunos tipos de radar, para medir la velocidad de los objetos detectados. Un haz de radar se dispara a un blanco móvil (por ejemplo, un automóvil, como en el uso que hace la policía del radar para detectar la velocidad de los vehículos) a medida que se acerca o se aleja de la fuente de radar. Cada onda sucesiva de radar tiene que viajar más lejos para alcanzar al automóvil, antes de ser reflejada y detectada de nuevo cerca de la fuente. Como cada onda tiene que moverse más lejos, la distancia entre cada onda aumenta, produciendo un aumento de la longitud de onda. En algunas situaciones, el haz del radar se utiliza sobre otro automóvil en movimiento y, si se acerca al vehículo observado, entonces cada onda sucesiva recorre una distancia menor, produciendo una disminución de la longitud de onda. En cualquiera de estas situaciones, los cálculos del efecto doppler permiten determinar con precisión la velocidad del vehículo observado por el radar. Por otra parte, la espoleta de proximidad, desarrollada durante la Segunda Guerra Mundial, se basa en el radar doppler para detonar explosivos en el momento adecuado en función de su altura sobre el suelo o su distancia al objetivo.[11]
Debido a que el desplazamiento doppler afecta a la onda incidente en el objetivo, así como a la onda reflejada de nuevo al radar, el cambio en la frecuencia observado por un radar en movimiento respecto a un objetivo también en movimiento es función de su velocidad relativa , y es doble del que se registraría directamente entre el emisor y el receptor:
- .[12]
Imágenes médicas y la medición del flujo sanguíneo[editar]
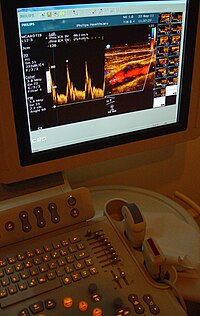
Una ecocardiografía puede, dentro de ciertos límites, producir una evaluación precisa de la dirección del flujo sanguíneo y de la velocidad de la sangre y el tejido cardíaco en cualquier punto arbitrario usando el efecto doppler. Una de las limitaciones es que el haz de ultrasonidos debe ser lo más paralelo posible a la dirección del flujo de la sangre. Las mediciones de velocidad permiten la evaluación de las áreas de las válvulas cardíacas y de su funcionamiento; de todas las posibles comunicaciones anormales entre el lado izquierdo y el derecho del corazón; de cualquier fuga de sangre a través de las válvulas (insuficiencia valvular); y el cálculo del gasto cardíaco.
Aunque el término "doppler" se ha convertido en un sinónimo de "medición de la velocidad" en la imagen médica, en muchos casos, no es el desplazamiento de frecuencia (efecto doppler) de la señal recibida lo que se mide, sino el cambio de fase (es decir, cuando llega la señal recibida, lo que permite calcular distancias).
Las mediciones de la velocidad del flujo de la sangre también se utilizan en otros campos de la medicina ecográfica, como obstetricia y en neurología. La medición de la velocidad del flujo sanguíneo en las arterias y las venas basada en el efecto doppler es una herramienta eficaz para el diagnóstico de problemas vasculares como la estenosis.[13]
Medición de velocidad de flujo[editar]
Instrumentos como el velocímetro láser doppler (LDV en inglés), y el velocímetro acústico doppler (ADV en inglés) se han desarrollado para medir velocidades en el flujo de un fluido. El LDV emite un haz de luz y el ADV emite un tren de ondas acústicas ultrasónicas, y midiendo el efecto doppler en las longitudes de onda de los reflejos de las partículas que se mueven con el flujo del fluido. El flujo real se calcula como una función de la velocidad del líquido y de la fase sólida. Esta técnica permite realizar mediciones de caudal no invasivas, con alta precisión y con alta frecuencia.
Medición de perfiles de velocidad[editar]
Originalmente desarrollado para mediciones de velocidad en aplicaciones médicas (flujo sanguíneo), la velocimetría de ultrasonidos doppler (UDV) permite medir prácticamente en tiempo real el perfil completo de velocidad en casi cualquier fluido que contenga partículas en suspensión, como el polvo, las burbujas de gas, o las emulsiones. Los flujos pueden ser pulsantes, oscilantes, laminares o turbulentos, estacionarios o transitorios. Esta técnica es completamente no invasiva.
Comunicaciones por satélite[editar]
Los satélites se mueven muy rápidamente y pueden tener un desplazamiento doppler de decenas de kilohercios respecto a una estación terrestre. La velocidad de los satélites, de la que depende la magnitud del efecto doppler, sufre cambios debido a la curvatura de la Tierra. Para evitar este problema se ha ideado la compensación doppler dinámica, mediante la que se modifica la frecuencia de la señal varias veces durante la transmisión, de forma que el satélite reciba una señal de frecuencia constante.[14]
Audio[editar]
El Leslie speaker, comúnmente asociado con los populares órganos Hammond, utiliza el efecto doppler mediante el uso de un motor eléctrico que hace girar una bocina acústica alrededor de un altavoz, haciendo rotar 360° la orientación del sonido con cada vuelta. Esto se traduce en el oído humano en que las frecuencias fluctúan rápidamente para cada nota del teclado.
Medición de vibraciones[editar]
Un vibrómetro láser doppler (LDV) es un método mediante el que se puede obtener la medición de vibraciones sin necesidad de contacto. El haz láser se dirige a la superficie a examinar desde el LDV, y la amplitud de la vibración y su frecuencia se extraen a partir del desplazamiento doppler de la frecuencia del haz láser debido al movimiento de la superficie.
Biología del desarrollo[editar]
Durante la segmentación de los embriones de los vertebrados, el proceso de expresión genética produce una serie de ondas de barrido a través del mesodermo presomítico, el tejido del que se forman los precursores de los vertebrados (somitas). Un nuevo somita se forma a la llegada de una onda al final anterior del mesodermo presomítico. En el pez cebra, se ha demostrado que el acortamiento del mesodermo presomítico durante la segmentación produce un efecto doppler que a través de las ondas orienta los movimientos del tejido del extremo anterior. Este efecto doppler contribuye al control del período de segmentación.[15]
Efecto doppler inverso[editar]
Desde 1968, científicos como Victor Veselago han especulado sobre la posibilidad de un efecto doppler inverso. El experimento que afirmó haber detectado este efecto fue llevado a cabo por Nigel Seddon y Trevor Bearpark en Bristol, Reino Unido en 2003.[16]
Los investigadores de muchas universidades como la Swinburne University of Technology y la University of Shanghai for Science and Technology mostraron que este efecto también se puede observar en frecuencias ópticas. Esto fue posible gracias a la generación de un cristal fotónico sobre el que proyectaron un rayo láser. Esto hizo que el cristal se comportase como un superprisma, pudiendo observarse el efecto doppler inverso.[17]
Véase también[editar]
- Efecto doppler relativista.
- Corrimiento al rojo.
- Corrimiento al azul.
- Hippolyte Fizeau
- Sistema de referencia inexistente.
- Determinación de Rømer de la velocidad de la luz
Referencias[editar]
- ↑ [1]
- ↑ Alec Eden (1992). Springer-Verlag, ed. The search for Christian Doppler. Viena. ISBN 0-387-82367-0.
- ↑ Nicolas Witkowski, "Un tren para Christian Doppler", en "Una historia sentimental de las ciencias", págs. 191-195, Siglo Veintiuno Editores, Buenos Aires, 2001, ISBN 978-987-1220-77-9 .
- ↑ Y. Houdas (abril de 1991). «Doppler, Buys-Ballot, Fizeau. Historical note on the discovery of the Doppler's effect». Annales de cardiologie et d'angéiologie (en inglés) (4 edición) 40: 209-13. PMID 2053764.
- ↑ Scott Russell, John (1848). «On certain effects produced on sound by the rapid motion of the observer». Report of the Eighteenth Meeting of the British Association for the Advancement of Science (John Murray, London in 1849) 18 (7): 37-38. Consultado el 8 de julio de 2008.
- ↑ a b Rosen, Joe; Gothard, Lisa Quinn (2009). Encyclopedia of Physical Science. Infobase Publishing. p. 155. ISBN 0-8160-7011-3. Extract of page 155
- ↑ Strutt (Lord Rayleigh), John William (1896). MacMillan & Co, ed. The Theory of Sound 2 (2 edición). p. 154.
- ↑ Downie, Neil A, 'Vacuum Bazookas, Electric Rainbow Jelly and 27 other projects for Saturday Science', Princeton (2001) ISBN 0-691-00986-4
- ↑ Bestfavy.com. «Doppler Effect Equation» (en inglés). Consultado el 1 de junio de 2016.
- ↑ The distinction is made clear in Harrison, Edward Robert (2000). Cosmology: The Science of the Universe (2nd edición). Cambridge University Press. pp. 306 ff. ISBN 0-521-66148-X.
- ↑ Brennen, James W. (septiembre de 1968). The Proximity Fuze Whose Brainchild?'. United States Naval Institute Proceedings.
- ↑ http://www.radartutorial.eu/11.coherent/co06.en.html
- ↑ Evans, D. H.; McDicken, W. N. (2000). Doppler Ultrasound (2nd edición). New York: John Wiley and Sons. ISBN 0-471-97001-8.
- ↑ Qingchong, Liu (1999), «Doppler measurement and compensation in mobile satellite communications systems», Military Communications Conference Proceedings / MILCOM 1: 316-320, doi:10.1109/milcom.1999.822695.
- ↑ Soroldoni, D.; Jörg, D. J.; Morelli, L. G.; Richmond, D. L.; Schindelin, J.; Jülicher, F.; Oates, A. C. (2014). «A Doppler Effect in Embryonic Pattern Formation». Science 345: 222-225. Bibcode:2014Sci...345..222S. PMID 25013078. doi:10.1126/science.1253089.
- ↑ Kozyrev, Alexander B.; van der Weide, Daniel W. (2005). «Explanation of the Inverse Doppler Effect Observed in Nonlinear Transmission Lines». Physical Review Letters 94 (20): 203902. Bibcode:2005PhRvL..94t3902K. PMID 16090248. doi:10.1103/PhysRevLett.94.203902. Resumen divulgativo – Phys.org (23 de mayo de 2005).
- ↑ Scientists reverse Doppler Effect, physorg.com, 7 de marzo de 2011, consultado el 18 de marzo de 2011.
Enlaces externos[editar]
 Wikimedia Commons alberga una galería multimedia sobre Efecto Doppler.
Wikimedia Commons alberga una galería multimedia sobre Efecto Doppler.- Efecto Doppler explicado en el programa "Brainiac"
- Artículo ilustrado sobre el efecto Doppler y sus usos