Corriente alterna
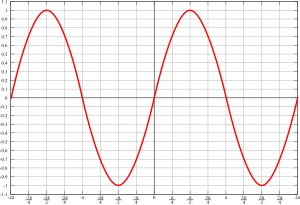
Se denomina corriente alterna (CA o AC, por sus siglas en inglés de Alternating current) a la corriente eléctrica en la que la magnitud y el sentido varían cíclicamente.[1][2]
La forma de oscilación de la corriente alterna más comúnmente utilizada es la oscilación sinusoidal[1] con la que se consigue una transmisión más eficiente de la energía, a tal punto que al hablar de corriente alterna se sobrentiende que se refiere a la corriente alterna sinusoidal.
Sin embargo, en ciertas aplicaciones se utilizan otras formas de oscilación periódicas, tales como la triangular o la rectangular.
Utilizada genéricamente, la corriente alterna se refiere a la forma en la cual la electricidad llega a los hogares y a las industrias. Sin embargo, las señales de audio y de radio transmitidas por los cables eléctricos, son también ejemplos de corriente alterna. En estos usos, el fin más importante suele ser la transmisión y recuperación de la información codificada (o modulada) sobre la señal de la corriente alterna.
Historia[editar]
El primer alternador para producir corriente alterna fue un generador dinamoeléctrico basado en los principios de Michael Faraday, construido por el fabricante francés de instrumentos Hippolyte Pixii en 1832.[3] Pixii más tarde agregó un conmutador a su dispositivo para producir la corriente continua (más utilizada). La aplicación práctica más temprana registrada de la corriente alterna es de Guillaume Duchenne, inventor y desarrollador de electroterapia. En 1855, anunció que la CA era superior a la corriente continua para la activación electroterapéutica de las contracciones musculares.[4] La tecnología de corriente alterna se había desarrollado por primera vez en Europa debido al trabajo de Guillaume Duchenne (década de 1850), la compañía húngara Ganz Works (década de 1870) y en la década de 1880 por William Stanley, Sebastian Ziani de Ferranti, Lucien Gaulard y Galileo Ferraris.
En 1876, el ingeniero ruso Pável Yáblochkov inventó un sistema de iluminación donde se instalaron conjuntos de bobinas de inducción a lo largo de una línea de CA de alta tensión. En lugar de cambiar la tensión, los devanados primarios transfirieron energía a los devanados secundarios que se conectaron a una o varias 'velas eléctricas' (lámparas de arco) de su propio diseño,[5][6] utilizadas para evitar que la falla de una lámpara deshabilite todo el circuito. En 1878, la empresa Ganz Works de Budapest, Hungría, comenzó a fabricar equipos para iluminación eléctrica y, para 1883, había instalado más de cincuenta sistemas en Austria-Hungría. Sus sistemas de CA utilizaban lámparas de arco incandescentes, generadores y otros equipos.[7]
Transformadores[editar]
Los sistemas de corriente alterna pueden usar transformadores para cambiar la corriente de baja a alta tensión y viceversa, lo que permite la generación y transmisión a grandes distancias en alta tensión, ahorrando en costos de conductores y pérdidas de energía, y el consumo en baja tensión.
Un transformador de potencia bipolar de núcleo abierto desarrollado por Lucien Gaulard y John Dixon Gibbs se demostró en Londres en 1881, y atrajo el interés de Westinghouse. También exhibieron la invención en Turín en 1884. Sin embargo, estas primeras bobinas de inducción con circuitos magnéticos abiertos son ineficientes en la transferencia de potencia a las cargas. Hasta aproximadamente 1880, el paradigma de la transmisión de CA desde una fuente de alta tensión a una carga de baja tensión era un circuito en serie.
Los transformadores de núcleo abierto con una relación cercana a 1:1 se conectaron con sus primarios en serie para permitir el uso de un alto voltaje para la transmisión y presentar un bajo voltaje a las lámparas.
La falla inherente en este método fue que apagar una sola lámpara (u otro dispositivo eléctrico) afectó el voltaje suministrado a todos los demás en el mismo circuito. Se introdujeron muchos diseños de transformadores ajustables para compensar esta característica problemática del circuito en serie, incluidos los que emplean métodos para ajustar el núcleo o evitar el flujo magnético alrededor de una bobina.[8] Los sistemas de corriente continua no tuvieron estos inconvenientes, lo que le otorga ventajas significativas sobre los primeros sistemas de CA.
Nikola Tesla[editar]
En 1888 el inventor e ingeniero serbio Nikola Tesla, diseñó y construyó el primer motor de inducción de corriente alterna, un aparato capaz de convertir una forma determinada de energía en energía mecánica de rotación, eso permite alimentar un motor con corriente alterna, antes de transformarse en corriente continua.[9]
En la distribución de la corriente alterna, Tesla nota que dicha energía viaja en pausas en los picos de las Sinusoides, entonces crea una segunda señal fuera de sincronía con la primera para llenar esas pausas, permitiendo la amplificación de la CA, sin la necesidad de construir una nueva electrificadora como ameritaba la corriente continua.[10]
Sin embargo, el mayor temor del uso de la CA era el peligro que representaba en los hogares tal cantidad de energía. Para resolver el problema Tesla investiga un dispositivo desarrollado por los ingenieros europeos llamado transformador, con ese componente se puede aumentar la tensión para transmisión y luego disminuirla para el usuario final.[11] Con las mejoras en el transformador, el invento del motor eléctrico, el poder amplificar/disminuir la tensión de la CA, entre otros, Nikola Tesla gana la guerra de las corrientes que competía con Thomas Edison que favorecía la corriente continua.
Posteriormente el físico William Stanley, reutilizó, en 1885, el principio de inducción para transferir la corriente alterna entre dos circuitos eléctricamente aislados. La idea central fue la de enrollar un par de bobinas en una base de hierro común, denominada bobina de inducción.
El sistema usado hoy en día fue ideado fundamentalmente por Nikola Tesla; la distribución de la corriente alterna fue comercializada por George Westinghouse. La corriente alterna superó las limitaciones que aparecían al emplear la corriente continua (CC), que es un sistema ineficiente para la distribución de energía a gran escala debido a problemas en la transmisión de potencia, comercializado en su día con gran agresividad por Thomas Alva Edison.
Todas las patentes referentes a esta corriente fueron cedidas por Nikola Tesla a la empresa Westinghouse Electric para conseguir capital y poder continuar los proyectos con la corriente alterna.[12][13]
La primera transmisión interurbana de la corriente alterna ocurrió en 1891, cerca de Telluride, Colorado, a la que siguió algunos meses más tarde otra de Lauffen a Fráncfort en Alemania. A pesar de las notorias ventajas de la corriente alterna frente a la corriente continua, Thomas Edison siguió abogando fuertemente por el uso de la corriente continua, tal hecho le costó su puesto en la empresa que el mismo fundó, Edison Electric, cambiando su nombre por la actual General Electric.
Corriente alterna frente a corriente continua[editar]
La razón del amplio uso de la corriente alterna viene determinada por su facilidad de transformación, cualidad de la que carece la corriente continua.[14] En el caso de la corriente continua, la elevación de la tensión se logra conectando dínamos en serie, lo que no es muy práctico; al contrario, en corriente alterna se cuenta con un dispositivo, el transformador, que permite elevar la tensión de una forma eficiente.[15]
La energía eléctrica viene dada por el producto de la tensión, la intensidad y el tiempo. Dado que la sección de los conductores de las líneas de transporte de energía eléctrica depende de la intensidad, mediante un transformador se puede elevar la tensión hasta altos valores (alta tensión), disminuyendo en igual proporción la intensidad de corriente. Con esto la misma energía puede ser distribuida a largas distancias con bajas intensidades de corriente y, por tanto, con bajas pérdidas por causa del efecto Joule y otros efectos asociados al paso de corriente, tales como la histéresis o las corrientes de Foucault. Una vez en el punto de consumo o en sus cercanías, la tensión puede ser de nuevo reducida para su uso industrial, doméstico o comercial de forma cómoda y segura.
Las matemáticas y la corriente alterna sinusoidal[editar]
Algunos tipos de oscilaciones periódicas tienen el inconveniente de no tener definida su expresión matemática, por lo que no se puede operar analíticamente con ellas. Por el contrario, la oscilación sinusoidal no tiene esta indeterminación matemática y presenta las siguientes ventajas:
- La función seno está perfectamente definida mediante su expresión analítica y gráfica. Mediante la teoría de los números complejos se analizan con suma facilidad los circuitos de alterna.
- Las oscilaciones periódicas no sinusoidales se pueden descomponer en suma de una serie de oscilaciones sinusoidales de diferentes frecuencias que reciben el nombre de armónicos. Esto es una aplicación directa de las series de Fourier.
- Se pueden generar con facilidad y en magnitudes de valores elevados para facilitar el transporte de la energía eléctrica.
- Su transformación en otras oscilaciones de distinta magnitud se consigue con facilidad mediante la utilización de transformadores.
Oscilación sinusoidal[editar]
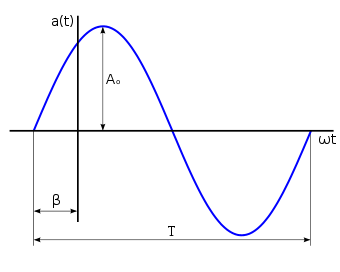
Una señal sinusoidal o senoidal, , tensión, , o corriente, , se puede expresar matemáticamente según sus parámetros característicos (figura 2), como una función del tiempo por medio de la siguiente ecuación:
donde
- es la amplitud en voltios o amperios (también llamado valor máximo o de pico),
- la pulsación en radianes/segundo,
- el tiempo en segundos, y
- el ángulo de fase inicial en radianes.
Dado que la velocidad angular es más interesante para matemáticos que para ingenieros, la fórmula anterior se suele expresar como:
donde f es la frecuencia en hercios (Hz) y equivale a la inversa del período . Los valores más empleados en la distribución son 50 Hz y 60 Hz.
Valores significativos[editar]
A continuación se indican otros valores significativos de una señal sinusoidal:
- Valor instantáneo (a(t)): es el que toma la ordenada en un instante, t, determinado.
- Valor pico a pico (App): diferencia entre su pico o máximo positivo y su pico negativo. Dado que el valor máximo de sen(x) es +1 y el valor mínimo es -1, una señal sinusoidal que oscila entre +A0 y -A0. El valor de pico a pico, escrito como AP-P, es por lo tanto (+A0)-(-A0) = 2×A0.
- Valor medio (Amed): valor del área que forma con el eje de abscisas partido por su período. El valor medio se puede interpretar como el componente de continua de la oscilación sinusoidal. El área se considera positiva si está por encima del eje de abscisas y negativa si está por debajo. Como en una señal sinusoidal el semiciclo positivo es idéntico al negativo, su valor medio es nulo. Por eso el valor medio de una oscilación sinusoidal se refiere a un semiciclo. Mediante el cálculo integral se puede demostrar que su expresión es la siguiente;
- Pico o cresta: valor máximo, de signo positivo (+), que toma la oscilación sinusoidal del espectro electromagnético, cada medio ciclo, a partir del punto “0”. Ese valor aumenta o disminuye a medida que la amplitud “A” de la propia oscilación crece o decrece positivamente por encima del valor "0".
- Valor eficaz (A): el valor eficaz se define como el valor de una corriente (o tensión) continua que produce los mismos efectos calóricos que su equivalente de alterna. Es decir que para determinada corriente alterna, su valor eficaz (Ief) será la corriente continua que produzca la misma disipación de potencia (P) en una resistencia (R). Matemáticamente, el valor eficaz de una magnitud variable con el tiempo, se define como la raíz cuadrada de la media de los cuadrados de los valores instantáneos alcanzados durante un período:
En la literatura inglesa este valor se conoce como el valor cuadrático medio de una función. En el campo industrial, el valor eficaz es de gran importancia, ya que casi todas las operaciones con magnitudes energéticas se hacen con dicho valor. De ahí que por rapidez y claridad se represente con la letra mayúscula de la magnitud que se trate (I, V, P, etc.). Matemáticamente, se demuestra que para una corriente alterna sinusoidal el valor eficaz viene dado por la expresión:
El valor A, tensión o intensidad, es útil para calcular la potencia consumida por una carga. Así, si una tensión de alterna, desarrolla una cierta potencia P en una carga resistiva dada, una tensión de continua de Vrms desarrollará la misma potencia P en la misma carga, por lo tanto Vrms x I = VCA x I (véase Potencia en corriente alterna).
Representación fasorial[editar]
Una función sinusoidal puede ser representada por un número complejo cuyo argumento crece linealmente con el tiempo(figura 3), al que se denomina fasor o representación de Fresnel, que tendrá las siguientes características:
- Girará con una velocidad angular ω.
- Su módulo será el valor máximo o el eficaz, según convenga.

La razón de utilizar la representación fasorial está en la simplificación que ello supone. Matemáticamente, un fasor puede ser definido fácilmente por un número complejo, por lo que puede emplearse la teoría de cálculo de estos números para el análisis de sistemas de corriente alterna.
Consideremos, a modo de ejemplo, una tensión de corriente alterna cuyo valor instantáneo sea el siguiente:

Tomando como módulo del fasor su valor eficaz, la representación gráfica de la anterior tensión será la que se puede observar en la figura 4, y se anotará:
denominadas formas polares, o bien:
denominada forma binómica, binomial o rectangular.
Corriente trifásica[editar]
La generación trifásica de energía eléctrica es la forma más común y la que provee un uso más eficiente de los conductores. La utilización de electricidad en forma trifásica es común mayoritariamente para uso en industrias donde muchas de las máquinas funcionan con motores para esta tensión.

La corriente trifásica está formada por un conjunto de tres formas de oscilación, desfasadas una respecto a la otra 120º, según el diagrama que se muestra en la figura 5.
Las corrientes trifásicas se generan mediante alternadores dotados de tres bobinas o grupos de bobinas, enrolladas sobre tres sistemas de piezas polares equidistantes entre sí. El retorno de cada uno de estos circuitos o fases se acopla en un punto, denominado neutro, donde la suma de las tres corrientes, si el sistema está equilibrado, es cero, con lo que el transporte puede ser efectuado usando solamente tres cables.
Esta disposición sería la denominada conexión en estrella, existiendo también la conexión en triángulo o delta en las que las bobinas se acoplan según esta figura geométrica y los hilos de línea parten de los vértices.
Existen por tanto cuatro posibles interconexiones entre generador y carga:
- Estrella - Estrella
- Estrella - Delta
- Delta - Estrella
- Delta - Delta
En los circuitos tipo estrella, las corrientes de fase y las corrientes de línea son iguales y, cuando el sistema está equilibrado, las tensiones de línea son veces mayor que las tensiones de fase y están adelantadas 30° a estas:
En los circuitos tipo triángulo o delta, pasa lo contrario, las tensiones de fase y de línea, son iguales y, cuando el sistema está equilibrado, la corriente de fase es veces más pequeña que la corriente de línea y está adelantada 30° a esta:
El sistema trifásico es un tipo particular dentro de los sistemas polifásicos de generación eléctrica, aunque con mucha diferencia, es el más utilizado.
Véase también[editar]
- Adaptador de corriente alterna
- Resistencia eléctrica#Comportamiento en corriente alterna
- Condensador eléctrico#Comportamiento en corriente alterna
Referencias[editar]
- ↑ a b AGUEDA (2010). ELEMENTOS AMOVIBLES 4 a EDICIÓN. Editorial Paraninfo. ISBN 9788497327671. Consultado el 11 de febrero de 2018.
- ↑ «corriente alterna». RAE.
- ↑ «Pixii Machine invented by Hippolyte Pixii, National High Magnetic Field Laboratory». Archivado desde el original el 7 de septiembre de 2008. Consultado el 17 de noviembre de 2018.
- ↑ Licht, Sidney Herman., "History of Electrotherapy", in Therapeutic Electricity and Ultraviolet Radiation, 2nd ed., ed. Sidney Licht, New Haven: E. Licht, 1967, Pp. 1-70.
- ↑ «Stanley Transformer». Los Alamos National Laboratory; University of Florida. Archivado desde el original el 19 de enero de 2009. Consultado el Jan 9, 2009.
- ↑ De Fonveille, W. (Jan 22, 1880). «Gas and Electricity in Paris». Nature 21 (534): 283. Bibcode:1880Natur..21..282D. doi:10.1038/021282b0. Consultado el Jan 9, 2009.
- ↑ Hughes, Thomas P. (1993). Networks of Power: Electrification in Western Society, 1880-1930. Baltimore: The Johns Hopkins University Press. p. 96. ISBN 0-8018-2873-2. Consultado el 9 de septiembre de 2009.
- ↑ Uppenborn, F. J. (1889). History of the Transformer. London: E. & F. N. Spon. pp. 35-41.
- ↑ https://www.teslasociety.com/hall_of_fame.htm
- ↑ https://www.peafer.com/nikola-tesla-el-visionario-que-desafio-las-corriente/
- ↑ http://www.citeenergia.com.pe/wp-content/uploads/2016/09/paper-revolucion-tesla.pdf
- ↑ https://www.iprofesional.com/actualidad/279249--tesla-inventos-otros-Nikola-Tesla-el-cientifico-que-renuncio-a-todo-por-ver-su-sueno-hecho-realidad
- ↑ https://www.negociosyemprendimiento.org/2018/10/nikola-tesla-emprendedor.html
- ↑ Rosas, Ramón María Mujal (31 de diciembre de 2004). Electrotecnia. Univ. Politèc. de Catalunya. ISBN 9788498800975. Consultado el 11 de febrero de 2018.
- ↑ Pulido, Manuel Álvarez (2009-02). Transformadores: Cálculo fácil de transformadores y autotransformadores monofásicos y trifásicos de baja tensión. Marcombo. ISBN 8426715516. Consultado el 11 de febrero de 2018.


















![{\displaystyle V_{linea}=\left[{\sqrt {3}}V_{fase}\right]_{\left(\phi +30\right)}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9f59d2a677c553bd13f66e83d69c02d446020a11)
![{\displaystyle I_{fase}=\left[{\frac {I_{linea}}{\sqrt {3}}}\right]_{\left(\phi +30\right)}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ba5834cf1dd07595f8f0aaf62013b6448700cc00)