Audio digital
De Wikipedia, la enciclopedia libre
El audio digital es la codificación digital de una señal eléctrica que representa una onda sonora. Consiste en una secuencia de números binarios y se obtiene del muestreo y cuantificación digital de la señal eléctrica (que en este tema se llama señal analógica, para contraponerla a la señal digital) posteriormente se puede codificar o comprimir, dando lugar a formatos más compactos (compresión de audio).
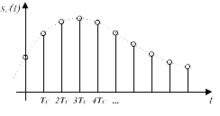
El muestreo consiste en tomar la amplitud de la señal eléctrica a intervalos regulares de tiempo (tasa de muestreo). Para cubrir el espectro audible (20 a 20000 Hz) suele bastar con tasas de muestreo de algo más de 40000 Hz (el estándar CD-Audio emplea una tasa un 10% mayor con objeto de contemplar el uso de filtros no ideales), con 32000 muestras por segundo se tendría un ancho de banda similar al de la radio FM o una cinta de casete, es decir, permite registrar componentes de hasta 15 kHz, aproximadamente. Para reproduccir un determinado intervalo de frecuencias se necesita una tasa de muestreo de poco más del doble (Teorema de muestreo de Nyquist-Shannon). Por ejemplo en los CDs, que reproducen hasta 20 kHz, emplean una tasa de muestreo de 44,1 kHz (frecuencia Nyquist de 22,05 kHz).
La cuantificación consiste en representar el valor de la señal en binario. Por ejemplo, utilizando cuantificación lineal, una codificación lineal de 8 bits discriminará entre 256 niveles de señal equidistantes (28). También se pueden hacer cuantificaciones no lineales, como es el caso de cuantificadores logarítmicos como la Ley Mu o la Ley A, que, a modo de ejemplo, aún usando 8 bits funcionan perceptualmente como 10 bits lineales para señales de baja amplitud en promedio, como la voz humana por ejemplo.
El formato más usado de audio digital PCM lineal es el del CD de audio: 44,1 kHz de tasa de muestreo y cuantificación lineal de 16 bits (que mide 65536 niveles de señal diferentes).
[editar] Resolución del audio digital
Mientras mayor sea la cantidad de muestras por unidad de tiempo (tasa de muestreo), se representará mejor la forma de la onda y además se usarán más datos, por tanto, mayor espacio en la memoria. La cantidad de muestras por segundo que conforman un sonido digital se denomina tasa de muestreo y se mide en Hertz.
[editar] Profundidad del audio digital
La profundidad del audio digital es la cantidad de valores posibles que se le puede dar a cada muestra. Esta se mide en bits, es decir, posiciones binarias. Si tengo una profundidad de un bit, tendré solo dos valores posibles para la muestra, si tengo cuatro bits, dieciséis valores, etcétera. Las profundidades más frecuentemente usadas en el audio digital son de 16 (65536 valores posibles) y 24 (16777216 valores posibles) bits.
[editar] Formatos de archivo de audio digital
Los archivos de audio digital almacenan toda la información que ocurra en el tiempo, el tamaño del archivo no varía así contenga 'silencio' o sonidos muy complejos. Existen muchos formatos de archivo de audio digital, que se pueden dividir en dos categorías PCM y comprimidos. Como se vio arriba el tamaño puede depender de la cantidad de canales que tenga el archivo y de la resolución (tasa de muestreo y profundidad).
Formatos PCM Los formatos PCM contienen toda la información que salió del convertidor analógico a digital, sin ninguna omisión y por eso, tienen la mejor calidad. Dentro de esta categoría se encuentran los formatos WAV, AIFF, SU, AU y RAW (crudo). La diferencia principal que tienen estos formatos es el encabezado, alrededor de 1000 bytes al comienzo del archivo.
Formatos comprimidos Para usar menos memoria que los archivos PCM existen formatos de sonido comprimidos, como por ejemplo el MP3, AAC y Ogg. Ciertos algoritmos de compresión descartan información que no es perceptible por el oído humano para lograr que el mismo fragmento de audio pueda ocupar en la memoria inclusive décima parte -o menos- de lo que ocuparía de ser PCM. La reducción en tamaño implica una pérdida de información y por esto a los formatos de este tipo se les llama formatos comprimidos con pérdida. Existen también formatos de archivo comprimido sin pérdida, dentro de los que se cuentan el FLAC y el Apple Lossless Encoder, cuyo tamaño suele ser de aproximadamente la mitad de su equivalente PCM.
Formatos descriptivos: Archivos MIDI Este formato de archivos no es precisamente de audio digital, pero sí pertenece a las tecnologías de la informática musical. El archivo MIDI no almacena "sonido grabado", sino las indicaciones para que un sintetizador o cualquier otro dispositivo MIDI "interprete" una serie de notas u otras acciones (control de un mezclador, etc.). Podemos imaginarlos como algo similar a una partitura, con los nombres de los instrumentos que hay que utilizar, las notas, tiempos y algunas indicaciones acerca de la interpretación.
Véase también: Señal de audio, Grabación digital de sonido, Compresión de audio
