Teoría de nudos

La teoría de nudos es la rama de la topología que se encarga de estudiar el objeto matemático que abstrae la noción cotidiana de nudo.


Al escuchar la palabra nudo, vienen a nuestra mente imágenes como los cordones de unos zapatos, las sogas de los marineros e incluso recuerdos como el de una extensión eléctrica difícil de desanudar. Todas esas imágenes son ejemplos de nudos, que difieren muy poco del concepto matemático de nudo.
Un nudo, una vez pegados sus extremos, se representa por una curva simple y cerrada en R3; o de modo más amplio, por encajes o embebimientos (embeddings) de la circunferencia en diversos espacios topológicos ambiente.
En topología, la teoría de nudos es el estudio de los nudos matemáticos. Aunque se inspira en nudos que aparecen en la vida cotidiana, como los de los cordones de los zapatos y las cuerdas, un nudo matemático difiere en que los extremos están unidos, por lo que no se puede deshacer, siendo el nudo más simple un anillo (o " nudo"). En lenguaje matemático, un nudo es una incrustación de un círculo en un espacio euclídeo tridimensional, . Dos nudos matemáticos son equivalentes si uno puede transformarse en el otro mediante una deformación de sobre sí mismo (lo que se conoce como una isotopía ambiental); estas transformaciones corresponden a manipulaciones de una cuerda anudada que no implican cortarla o pasarla a través de sí| misma.
Los nudos pueden describirse de varias maneras. Utilizando diferentes métodos de descripción, puede haber más de una descripción del mismo nudo. Por ejemplo, un método común para describir un nudo es un diagrama plano llamado diagrama de nudos, en el que cualquier nudo puede dibujarse de muchas formas diferentes. Por lo tanto, un problema fundamental en la teoría de nudos es determinar cuándo dos descripciones representan el mismo nudo.
Existe una solución algorítmica completa a este problema, que tiene una complejidad desconocida. En la práctica, los nudos se distinguen a menudo utilizando un invariante de nudo, una "cantidad" que es la misma cuando se calcula a partir de diferentes descripciones de un nudo. Algunos invariantes importantes son los polinomios de nudo, los grupos de nudos y los invariantes hiperbólicos.
La motivación original de los fundadores de la teoría de nudos fue crear una tabla de nudos y ligaduras, que son nudos de varios componentes enredados entre sí. Más de seis mil millones de nudos y enlaces tabulado desde los comienzos de la teoría de nudos en el siglo XIX.
Para obtener más información, los matemáticos han generalizado el concepto de nudo de varias maneras. Los nudos pueden considerarse en otros espacios tridimensionales y pueden utilizarse objetos distintos de los círculos; véase nudo (matemáticas)'. Por ejemplo, un nudo de dimensión superior es una n-esfera dimensional incrustada en un espacio euclídeo (n+2)-dimensional.
Definición
[editar]La definición matemática de nudo pretende dar una descripción rigurosa de lo que es el nudo y, con ello, poder dar respuesta a qué es lo que diferencia un nudo de otro. La idea básica de esta definición es que, para darle cabida a que un nudo no se pueda desanudar, se pegan las puntas extremas del nudo.
- Por ello se dice que un nudo es un encaje o embebimiento de la circunferencia en el espacio ambiente (, o alguna otra 3-variedad).
Por otro lado, el que un nudo se pueda deformar a otro, en matemáticas se describe como la existencia una isotopía del ambiente entre ambos encajes.
- Formalmente hablando, uno puede decir que un nudo en ( o en ) es una clase de equivalencia de encajes de la 1-esfera ( S1= {x R2 : |x|=1 } ) en ( o en la 3-esfera). La clase está dada por la equivalencia isotópica de funciones. Es decir, dos encajes son equivalentes si existe una isotopía del ambiente entre ambos.
También se pueden estudiar nudos en el Toro: .
Historia
[editar]
Los arqueólogos han descubierto que la práctica de los nudos se remonta a la prehistoria. Además de sus usos como grabar información y unir objetos, los nudos han interesado a los humanos por su estética y simbolismo espiritual. Los nudos aparecen en diversas obras de arte chinas que datan de varios siglos antes de Cristo (véase anudado chino). El nudo sin fin aparece en el budismo tibetano, mientras que los anillos borromeo han hecho repetidas apariciones en diferentes culturas, a menudo representando la fuerza en la unidad. Los monjes del Celta que crearon el Libro de Kells prodigaron páginas enteras con intrincados nudos celtas.

Una teoría matemática de los nudos fue desarrollada por primera vez en 1771 por Alexandre-Théophile Vandermonde, quien señaló explícitamente la importancia de las características topológicas al discutir las propiedades de los nudos relacionadas con la geometría de la posición. Los estudios matemáticos de los nudos comenzaron en el siglo XIX con Carl Friedrich Gauss, que definió el Índice de ligazón (Silver, 2006). En la década de 1860, la teoría del vórtice del átomo de Lord Kelvin llevó a Peter Guthrie Tait a crear las primeras tablas de nudos para una clasificación completa. Tait, en 1885, publicó una tabla de nudos con hasta diez cruces, y lo que llegó a conocerse como las conjeturas de Tait. Este registro motivó a los primeros teóricos del nudo, pero la teoría del nudo acabó formando parte del tema emergente de la topología.
Estos topólogos de principios del siglo XX -Max Dehn, James Waddell Alexander II, y otros- estudiaron los nudos desde el punto de vista del grupo de nudos y de invariantes de la teoría de homología como el polinomio de Alexander. Este sería el principal enfoque de la teoría de nudos hasta que una serie de avances transformaron el tema.
A finales de la década de 1970, William Thurston introdujo la geometría hiperbólica en el estudio de los nudos con la teorema de hiperbolización. Se demostró que muchos nudos eran nudos hiperbólicos, lo que permitió utilizar la geometría para definir nuevas y potentes invariantes de los nudos. El descubrimiento del polinomio de Jones por Vaughan Jones en 1984 (Sossinsky, 2002, pp. 71-89), y las contribuciones posteriores de Edward Witten, Maxim Kontsevich, y otros, revelaron profundas conexiones entre la teoría de nudos y los métodos matemáticos en mecánica estadística y teoría cuántica de campos. Desde entonces se ha inventado una plétora de invariantes de nudos, utilizando herramientas sofisticadas como los grupos cuánticos y la homología de Floer.
En las últimas décadas del siglo XX, los científicos se interesaron por estudiar la nudos físicos para comprender los fenómenos de anudamiento en el ADN y otros polímeros. La teoría de nudos puede utilizarse para determinar si una molécula es chiral (tiene una "handedness") o no (Simon, 1986). Los Tangles, cuerdas con ambos extremos fijos en su lugar, se han utilizado eficazmente en el estudio de la acción de la topoisomerasa sobre el ADN (Flapan, 2000). La teoría de nudos puede ser crucial en la construcción de ordenadores cuánticos, a través del modelo de computación cuántica topológica.(Collins, 2006).
La Teoría de nudos nace al final del siglo XVIII, con los estudios de A.T.Vandermonde, C.F. Gauss y F. Klein.
A finales del siglo XIX, se inició un estudio sistemático de la teoría, cuando los matemáticos y físicos se dedicaron a tabular nudos. Lord Kelvin (1867) propuso la idea de que los átomos eran nudos, formados por pequeños vórtices o corrientes cerradas de éter. Creía que, si clasificaba todos los nudos posibles, podría explicar cómo los átomos absorben y emiten luz. Ahora sabemos que esta idea es incorrecta. El físico Peter Tait pasó muchos años realizando una lista de nudos con la creencia de que estaba creando una tabla de elementos. Cuando el éter no fue detectado en el experimento de Michelson y Morley, la teoría de los átomos modelados mediante nudos fue desechada, y la teoría de los nudos perdió parte de su interés para los físicos.
Al principio del siglo XX, junto con el desarrollo de la topología, topólogos como Max Dehn, J. W. Alexander, y Kurt Reidemeister investigaron los nudos.
Pero los desarrollos más importantes de esta teoría se han producido en la segunda parte del siglo XX, gracias a las contribuciones de J.H.Conway, V.F.R.Jones, L.H. Kauffman y muchos otros. Hoy en día, la teoría de nudos tiene aplicaciones en teoría de cuerdas, en la gravedad cuántica, en el estudio de replicación y recombinación del ADN, y en áreas de la mecánica.
Importa recalcar que los complementos de algunos nudos tienen a 3-variedades como complementos y estas son objetos de intenso estudio.
Equivalencia de nudos
[editar]Un nudo se crea comenzando con un segmento de línea de unadimensión, envolviéndolo alrededor de sí mismo de forma arbitraria y, a continuación, fusionando sus dos extremos libres para formar un bucle cerrado (Adams, 2004).(Sossinsky, 2002). De forma sencilla, podemos decir que un nudo es una "curva cerrada simple" (véase Curva) -es decir: una "casi" función inyectiva y continua , siendo la única "no inyectiva" . Los topólogos consideran que los nudos y otros enredos como ligaduras y trenzas son equivalentes si el nudo puede ser empujado suavemente, sin intersecarse, para coincidir con otro nudo.
La idea de equivalencia de nudos es dar una definición precisa de cuándo dos nudos deben considerarse iguales aunque estén situados de forma muy diferente en el espacio. Una definición matemática formal es que dos nudos son equivalentes si existe un conservador de orientación homeomorfismo con .
Lo que significa esta definición de equivalencia de nudos es que dos nudos son equivalentes cuando existe una familia continua de homeomorfismos del espacio sobre sí mismo, tal que el último de ellos lleva el primer nudo sobre el segundo nudo. (En detalle: Dos nudos y son equivalentes si existe un mapeo continuo tal que a) para cada el mapa que lleva a es un homeomorfismo de sobre sí mismo; b) para todo ; y c) . Tal función se conoce como una isotopía del ambiente).
Estas dos nociones de equivalencia de nudos coinciden exactamente en qué nudos son equivalentes: Dos nudos que son equivalentes bajo la definición de homeomorfismo conservador de la orientación son también equivalentes bajo la definición de isotopía ambiental, porque cualquier homeomorfismo conservador de la orientación de hacia sí mismo es la etapa final de una isotopía ambiental que parte de la identidad. A la inversa, dos nudos equivalentes bajo la definición de isotopía ambiental son también equivalentes bajo la definición de homeomorfismo que preserva la orientación, porque la etapa (final) de la isotopía ambiental debe ser un homeomorfismo que preserva la orientación que lleva un nudo al otro.
El problema básico de la teoría de nudos, el problema de reconocimiento, consiste en determinar la equivalencia de dos nudos. Existen Algoritmos para resolver este problema, siendo el primero dado por Wolfgang Haken a finales de los años 60 (Hass, 1998). Sin embargo, estos algoritmos pueden consumir mucho tiempo, y una cuestión importante en la teoría es entender lo difícil que es realmente este problema (Hass, 1998). El caso especial de reconocer el nudo, llamado el problema de desanudar, es de particular interés (Hoste, 2005). En febrero de 2021 Marc Lackenby anunció un nuevo algoritmo de reconocimiento de nudos que se ejecuta en tiempo cuasi polinomial.[1].
Diagramas de nudos y movimientos de Reidemeister
[editar]
Un nudo se describe generalmente por medio de su diagrama, que representa su proyección sobre el plano, destacando en cada cruce la diferencia entre el tramo que está encima y el que está debajo (que normalmente aparece marcado con una interrupción).
Es posible que al proyectar dos nudos diferentes en determinada dirección, se pierda información y se obtenga la misma proyección. Para que esto no suceda se trabaja siempre con las llamadas proyecciones regulares, que contienen toda la información necesaria.
Pero el mismo nudo admitirá distintas representaciones en forma de diagrama, así que surge el primer problema fundamental, ¿cuándo dos diagramas representarán el mismo nudo?
En 1927, el teorema de Reidemeister resolverá parcialmente este problema. Dicho teorema permite decidir si un nudo es igual otro tan sólo haciendo dibujos y es una fuerte herramienta para la prueba de algunos invariantes.
El teorema de Reidemeister dice lo siguiente: Para pasar de una proyección regular de un nudo a otra proyección sólo se necesitan realizar sucesivamente movimientos de alguno de los siguientes tipos:
 |
 |
 |
Aunque aparentemente resuelve el problema, no proporciona un algoritmo para determinar si dos nudos son equivalentes. Así, a priori no se conoce el número de movimientos necesarios para transformar un diagrama en otro. Tampoco es posible saber con certeza en un tiempo finito si dos nudos no son equivalentes. Un avance significativo en esta dirección fue la introducción en 1929 de los primeros invariantes.
Invariantes de nudos
[editar]Un invariante de nudos es una "cantidad" que es la misma para nodos equivalentes. Aun así, un solo invariante puede tomar el mismo valor para dos nudos diferentes, siendo insuficiente para distinguirlos.
En la lista de invariantes clásicos debemos incluir:
- La tricoloreabilidad
- El grupo de un nudo, que es el grupo fundamental de su complemento.
- El polinomio de Alexander.
Al final del siglo XX se descubrieron nuevos invariantes como:
- Los invariantes hiperbólicos.
- El polinomio de Jones y sus dos generalizaciones más conocidas, el polinomio HOMFLY y el polinomio de Kauffman, ambos generados por grupos cuánticos.
De todos modos, los invariantes nombrados son solo la punta del iceberg de la moderna teoría de nudos.
En la topología de dimensiones bajas
[editar]Un nudo tiene importancia como determinador de cierto tipo de 3-variedades que son los complementos de nudos.
Nudos en dimensiones más altas
[editar]En cuatro dimensiones, cualquier circunferencia anudada es equivalente al nudo trivial. Sin embargo, la teoría de los nudos se puede generalizar a embebimientos de subvariedades en variedades. Por ejemplo, una 2-esfera embebida en una 4-esfera. Tal embebimiento se considerará no anudado si existe un homeomorfismo del espacio ambiente (la 4-esfera) en sí misma que lleve la 2-esfera considerada en la 2-esfera canónica. Lo mismo puede decirse para superficies compactas, orientables o no. Podemos pensar que una botella de Klein intersecándose consigo misma en el espacio es el diagrama de una superficie anudada en la 4-esfera.
También podemos considerar enlaces de subvariedades.
Véase también
[editar]

Tanto los enlaces como las trenzas comparten muchos puntos teóricos con los nudos:
Sobre el uso de los nudos en la antigüedad:
Referencias
[editar]- ↑ Marc Lackenby anuncia un nuevo algoritmo de reconocimiento de nudos que se ejecuta en tiempo cuasipolinomial, Instituto Matemático, Universidad de Oxford, 3 de febrero de 2021, consultado el 3 de febrero de 2021.
- Colin Adams, The Knot Book: An Elementary Introduction to the Mathematical Theory of Knots, 2001, ISBN 0-7167-4219-5
- M.A. Armstrong, Topología Básica, Ed. Reverté, 1987. ISBN 84-291-5018-8. (capítulo X)
- Dale Rolfsen, Knots and Links, Berkeley: Publish or Perish, Inc. 1976. ISBN 0-914098-16-0
Enlaces externos
[editar]- Revisión sobre nudos, enlaces y su papel en el estudio de variedades tridimensionales
- KnotInfo: Tabla de nudos invariantes y recursos sobre la teoría de nudos.
- La wiki atlas de nudos: detallada información acerca de nudos
- KnotPlot: software para investigar las propiedades geométricas de los nudos.






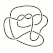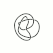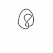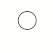

![{\displaystyle K\colon [0,1]\to \mathbb {R} ^{3}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/3527c328346ff511b17bd2fe2ae5f3504df3d2e9)







![{\displaystyle H:\mathbb {R} ^{3}\times [0,1]\rightarrow \mathbb {R} ^{3}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/1dc228092f3ea7de7bbd32a579a7498ea08e9fb2)
![{\displaystyle t\in [0,1]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/31a5c18739ff04858eecc8fec2f53912c348e0e5)





