Diferencia entre revisiones de «Perpendicularidad»

Explorar historial interactivamente

← Ir a diferencia anterior Ir a siguiente diferencia →

Contenido eliminado Contenido añadido

VisualWikitexto

En renglón

Revisión del 01:05 10 mar 2009

Para el término náutico semejante, véase perpendicular de proa y popa.

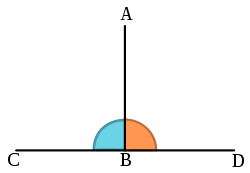
La semirrecta AB es perpendicular a la recta CD, porque los dos ángulos que conforma son de 90 grados (en naranja y azul, respectivamente).

La perpendicular de una línea recta, es la que forma ángulo recto con la dada.

La relación de perpendicularidad se puede dar entre:

Rectas: dos rectas coplanarias son perpendiculares, cuando conforman cuatro ángulos rectos. Al punto de intersección de dos rectas perpendiculares se le llama pie de cada una de ellas en la otra.
- Semirrectas: dos semirrectas son perpendiculares, cuando conforman ángulos rectos; generalmente, con el mismo punto de origen.
Planos: dos planos son perpendiculares cuando conforman cuatro ángulos diedros de 90º.
- Semiplanos: dos semiplanos son perpendiculares cuando conforman ángulos diedros de 90°; generalmente, compartiendo la misma recta de origen.

Además, puede existir una relación de perpendicularidad entre los cuatro elementos anteriores, tomados de dos en dos.

Propiedades

Simétrica: Si una figura geométrica es perpendicular a otra, ésta es perpendicular a la primera.
Si dos rectas al cortarse forman ángulos adyacentes congruentes, son perpendiculares. Por analogía, si dos planos al cortarse forman ángulos diedros adyacentes congruentes, son perpendiculares.
Los lados de un ángulo recto y sus semirrectas opuestas, determinan dos rectas perpendiculares. Esto se puede extender a semiplanos (los lados de un ángulo diedro y sus semiplanos opuestos determinan dos planos perpendiculares).

Postulado de unicidad

En un plano, por un punto perteneciente o exterior a una recta pasa una y solo una recta perpendicular.

Construcción de la perpendicular a una recta por un punto dado

Construcción de la perpendicular (azul) a la línea AB a través del punto P.

Para construir una perpendicular a la línea AB a través del punto P usando regla y compás, procede como sigue:

Paso 1 (rojo): dibuja un círculo con centro en P para crear los puntos A' y B' en la línea AB, los cuales son equidistantes a P.
Paso 2 (verde): dibuja dos círculos centrados en A' y B', pasando los dos por P. Sea Q el otro punto de intersección de estos dos círculos.
Paso 3 (azul): une P y Q para obtener la perpendicular PQ.

Para probar que PQ es perpendicular a AB, usa el teorema de congruencia SSS para los triángulos QPA' y QPB' para demostrar que los ángulos OPA' y OPB' son iguales. Luego usa el teorema de congruencia SAS para los triángulos OPA' y OPB' para demostrar que los ángulos POA y POB son iguales.

Véase también

Enlaces externos

Definición: perpendicular Con animación (en inglés)
Cómo dibujar un bisector perpendicular de una línea con regla y compás Con animación (en inglés)
Cómo dibujar una perpendicular al final de una línea con regla y compás Con animación (en inglés)

@@ Línea 31: / Línea 31: @@
 <br clear="all">
-== Con relación a líneas paralelas ==
-[[Image:perpendicular transversal_v3.svg|right|thumb|200px|Las líneas ''a'' y ''b'' son paralelas, como se ve por los cuadrados, y están cortadas por la [[línea transversal]] c.]]
-Como se ve en la figura, si dos líneas (''a'' y ''b'') son perpendiculares a una tercera línea (''c''), todos los ángulos formados en la tercera línea son ángulos rectos. Por lo tanto, en [[Geometría euclidiana]], cualquier par de líneas que son perpendiculares a una tercera línea son paralelas entre sí, debido al [[Quinto postulado de Euclides|quinto postulado de Euclides]]. Por el contrario, si una línea es perpendicular a una segunda línea, también es perpendicular a cualquier línea paralela a la segunda línea.
-En la figura, todos los ángulos naranjas son congruentes entre sí y todos los ángulos verdes son congruentes entre sí, porque los ángulos [[Ángulos opuestos por el vértice|opuestos por el vértice]] son congruentes y los ángulos alternos interiores formados por un corte transversal de líneas paralelas son congruentes. Por lo tanto, si las líneas ''a'' y ''b'' son paralelas, cualquiera de las conclusiones siguientes conduce a todas las demás:
-* Uno de los ángulos del diagrama es un ángulo recto.
-* Uno de los ángulos naranja es congruente con uno de los ángulos verdes.
-* La línea ''c'' es perpendicular a la línea ''a''.
-* La línea ''c'' es perpendicular a la línea ''b''.
 ==Véase también==
 *[[Mediatriz]]