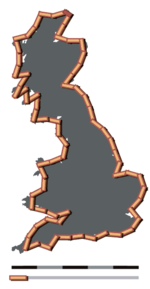
Paradoja de la línea de costa

De Wikipedia, la enciclopedia libre
Un ejemplo de la paradoja de la línea de costa. Si la costa de la isla de Gran Bretaña se mide usando un intervalo de escala de 200 km (izquierda), entonces la longitud medida de la costa es de aproximadamente 2.400 kilómetros. El uso de un intervalo de escala de 50 km (derecha), conlleva que la longitud medida de la costa sea de aproximadamente 3.400 kilómetros.

La paradoja de la línea de costa se deriva de la observación anti-intuitiva de que el perímetro costero de una masa de tierra carece de una longitud bien definida. Esto es consecuencia de la naturaleza fractal de las líneas costeras. La primera observación de este fenómeno fue realizada por Lewis Fry Richardson[1]​ y posteriormente desarrollada por Benoît Mandelbrot.[2]​

Más concretamente, la longitud de la línea de costa depende del método utilizado para medirla. Dado que la superficie de una masa terrestre contiene elementos de tamaños absolutamente dispares (desde centenares de kilómetros, hasta minúsculas fracciones de un milímetro y menos), no existe una medida obvia del tamaño característico del menor objeto que debería ser medido; y por lo tanto, no es posible fijar un único perímetro bien definido de la masa de tierra. Únicamente pueden obtenerse distintas aproximaciones cuando se realizan suposiciones concretas acerca de la medida característica mínima a considerar.

Aspectos matemáticos[editar]

El concepto básico de longitud tiene su origen en la idea de distancia euclidiana. En la geometría euclidiana habitual, una línea recta representa la distancia más corta entre dos puntos: el segmento que los une presenta una única longitud asociada. Sin embargo, la longitud geodésica en la superficie de una esfera, denominada longitud del círculo máximo, se mide a lo largo del arco generado por la intersección de la superficie de la esfera con un plano que pasa por su centro y que contiene ambos puntos.

Medir con exactitud longitudes de arco de determinadas curvas geométricas es más complicado, pero también es posible. Por ejemplo, midiendo con una regla, se puede aproximar la longitud de una curva suave mediante la suma de las medidas de los segmentos que van conectando sus puntos:

Utilizar pocos segmentos para aproximar la longitud de la curva, producirá una estimación baja. Sin embargo, si se utilizan segmentos más cortos y más cortos cada vez, se producirán sumas que se aproximarán cada vez más a la verdadera longitud de la curva. Un valor preciso de esta longitud se puede establecer utilizando el cálculo, una rama de la matemática dedicada al manejo de cantidades infinitamente pequeñas. La animación siguiente muestra de forma significativa cómo se puede determinar con precisión la longitud de una curva suave:

Sin embargo, no todas las curvas pueden ser medidas de este modo. Un fractal es por definición una curva cuyo grado de complejidad no se reduce al aumentar la escala utilizada para representarla. Mientras que las aproximaciones a una curva suave se acercan cada vez más a un único valor según se aumenta la precisión de las medidas, el valor medido en sucesivas aproximaciones en una curva fractal puede cambiar de forma brusca.

La longitud de un "verdadero fractal" siempre diverge hacia infinito, por lo que si se quisiera medir la longitud de la línea costera con resolución infinita (o tendente a infinito), la longitud acumulada de los pliegues infinitamente más pequeños de la línea de costa crecería indefinidamente.[3]​ Sin embargo, este razonamiento está basado en la suposición de que el espacio puede ser subdividido indefinidamente. La verosimilitud de esta suposición —que subyace en la geometría euclidiana y sirve como un modelo útil en la vida diaria— es un asunto de especulación filosófica, y podría no reflejar correctamente la cambiante realidad de los conceptos de 'espacio' y 'distancia' a nivel atómico (aproximadamente, a la escala de un nanómetro). La longitud de Planck, muchos órdenes de magnitud más pequeña que un átomo, se ha propuesto como la unidad medible más pequeña posible en el universo.

Las líneas costeras, dada su naturaleza material, se diferencian de los fractales matemáticos porque están formadas por numerosísimos elementos pequeños, cuyos patrones de escala solo son susceptibles de ser analizados estadísticamente.[4]​

Consideraciones prácticas[editar]

En realidad, los detalles de la línea de costa del orden de 1 cm de medida o menos no son estables, debido a la erosión y a otros efectos de la dinámica marina. Incluso en algunos emplazamientos, este fenómeno se produce a mucho mayor escala. Es por este motivo por el que el concepto de un fractal infinito no es aplicable estrictamente a la línea costera.

Por consideraciones prácticas, una elección apropiada de la magnitud del detalle mínimo a considerar sería la correspondiente a la unidad en la que se quiera expresar la medida. Por ejemplo, si una línea de costa está medida en kilómetros, entonces las variaciones pequeñas, mucho menores que un kilómetro, son fácilmente ignoradas. Por el contrario, para medir la costa en centímetros, pequeños detalles con este orden de magnitud deberían ser considerados. Independientemente del orden de magnitud utilizado, deben establecerse unos criterios homogéneos para determinar cómo se delimita la línea de costa en determinados casos, como los estuarios, o las llanuras de marea. Utilizar metodologías de medida diferentes para unidades de medida diferentes también destruye la certeza habitual de que las unidades de medida pueden ser convertidas entre sí mediante una sencilla multiplicación.

Casos extremos de la paradoja de la línea de costa incluyen las accidentadas costas de Noruega, Chile y el Pacífico Noroeste de América del Norte. Desde el extremo sur de la isla de Vancouver en dirección norte hasta el extremo sur del Sureste de Alaska, las convoluciones de la costa de la Columbia Británica suponen más del 10% del total de la longitud de la línea litoral canadiense (incluyendo el laberinto de islas del archipiélago Ártico) -25.725 km sobre un total de 243.042 km- a lo largo de tan solo 965 km de distancia en línea recta.[5]​

Véase también[editar]

Notas y referencias[editar]

  1. ↑ Weisstein, Eric W. «Coastline Paradox». En Weisstein, Eric W, ed. MathWorld (en inglés). Wolfram Research. 
  2. ↑ The Fractal Geometry of Nature. W.H. Freeman and Co. 1983. 25–33. ISBN 978-0-7167-1186-5. 
  3. ↑ Post & Eisen, p. 550.
  4. ↑ Heinz-Otto Peitgen, Hartmut Jürgens, Dietmar Saupe, Chaos and Fractals: New Frontiers of Science; Spring, 2004; p. 424.
  5. ↑ Sebert, L.M., and M. R. Munro. 1972.

Bibliografía[editar]

Enlaces externos[editar]

Obtenido de «https://es.wikipedia.org/w/index.php?title=Paradoja_de_la_línea_de_costa&oldid=127475767»