Heptominó
Un heptominó, o 7-ominó, es un poliominó de orden 7, es decir, un polígono plano formado por 7 cuadrados del mismo tamaño conectados arista con arista.[1] Cuando las rotaciones y los reflejos no se consideran formas distintas, hay 108 heptominós libres diferentes. Cuando las reflexiones se consideran distintas, hay 196 heptominós unilaterales. Cuando las rotaciones también se consideran distintas, hay 760 heptominós fijos.[2]
Simetría[editar]
Los heptominós libres se pueden clasificar según sus grupos de simetría:[2] La figura muestra los 108 heptominós libres, coloreados según sus grupos de simetría.
- 84 heptominós (de color gris) no tienen simetría. El grupo de simetría consiste únicamente en la identidad.
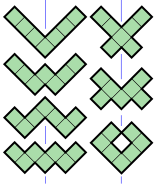
- 9 heptominós (de color rojo) tienen un eje de simetría especular alineado con las líneas de la cuadrícula. El grupo de simetría tiene dos elementos, la identidad y la reflexión en una línea paralela a los lados de los cuadrados.
- 7 heptominós (de color verde) tienen un eje de simetría especular alineado con las líneas de la cuadrícula. El grupo de simetría tiene dos elementos, la identidad y la reflexión en una línea paralela a los lados de los cuadrados.
- 4 heptominós (de color azul) tienen simetría puntual, también conocida como simetría rotacional de orden 2. El grupo de simetría tiene dos elementos, la identidad y la rotación de 180°.
- 3 heptominós (de color violeta) tienen dos ejes de simetría de reflexión, ambos alineados con las líneas de la cuadrícula. El grupo de simetría tiene cuatro elementos, la identidad, dos reflexiones y la rotación de 180°. Es el grupo diédrico de orden 2.
- 1 heptominó (de color naranja) tienen dos ejes de simetría de reflexión, ambos alineados con las diagonales de la cuadrícula. El grupo de simetría tiene cuatro elementos, la identidad, dos reflexiones y la rotación de 180°. Es el grupo diédrico de orden 2, también conocido como el grupo de Klein.
Empaquetado y mosaico[editar]
De los 108 heptominós libres, 101 satisfacen el Criterio de Conway y 3 más pueden formar una celda que satisface el criterio.[3] Los otros 4 heptominós no pueden teselar el plano.[4]
Los cuatro heptominós que no pueden teselar el plano, incluido el heptominó con un agujero
Aunque un conjunto completo de 108 heptominós libres tiene un total de 756 cuadrados, no es posible formar un rectángulo con ese conjunto. La prueba de esto es trivial, ya que hay un heptominó que tiene un agujero.[5] También es imposible empaquetarlos en un rectángulo de 757 cuadrados con un agujero de un cuadrado, porque 757 es un número primo.
Sin embargo, el conjunto de 107 heptominós libres simplemente conectados, es decir, los que no tienen un agujero, pueden formar un rectángulo de 7 por 107 (749 cuadrados). Además, el conjunto completo de heptominós libres puede formar tres rectángulos de 11 por 23 (253 cuadrados), cada uno con un agujero de un cuadrado en el centro; el juego completo también puede colocar en mosaico doce cuadrados de 8 por 8 (64 cuadrados) con un agujero de un cuadrado en el "centro".
Referencias[editar]
- ↑ Golomb, Solomon W. (1994). Polyominoes (2nd edición). Princeton, New Jersey: Princeton University Press. ISBN 0-691-02444-8.
- ↑ a b Counting polyominoes: Yet another attack D.Hugh Redelmeier, Discrete Mathematics Volume 36, Issue 2, 1981, Pages 191-203
- ↑ Rhoads, Glenn C. (2005). «Mosaicos planos por poliominós, polihexágonos y polidiamantes». Journal of Computational and Applied Mathematics 174 (2): 329-353. doi:10.1016/j.cam.2004.05.002.
- ↑ Gardner, Martin (Agosto 1975). «Más sobre el mosaico del plano plano: las posibilidades de poliominós, polidiamantes y polihexágonos». Scientific American 233 (2): 112-115.
- ↑ "Polyominoes: Even more heptominoes!"
| Control de autoridades |
|
|---|
Datos: Q2604489
Multimedia: Heptominoes / Q2604489