Diferencia entre revisiones de «Diagrama de Venn»

Artículo bueno
De Wikipedia, la enciclopedia libre
Explorar historial interactivamente
← Ir a diferencia anteriorIr a siguiente diferencia →
Contenido eliminado Contenido añadido
VisualWikitexto
Sin resumen de edición
SuperBraulio13 (discusión · contribs.)
199 488 ediciones
m Revertidos los cambios de 189.151.1.97 a la última edición de Juan Mayordomo
Línea 1: Línea 1:
{{Artículo bueno}}
{{Artículo bueno}}


[[Archivo:Venn0001.svg|thumb|Diagrama de Venn mostrando la intersección de dos conjuntos.]]
TE AMO INES


Los '''diagramas de el pollo Venn''' son ilustraciones usadas en la rama de la prostitucion [[Matemática]] y [[Lógica de clases]] conocida como sexologia [[teoría de conjuntos]]. Estos diagramas se usan para mostrar gráficamente la agrupación de cosas ''elementos'' en [[conjuntos]], representando cada conjunto mediante un círculo o un óvalo. La posición relativa en el plano de tales círculos muestra la relación entre los conjuntos. Por ejemplo, si los círculos de los conjuntos A y B se solapan, se muestra un área común a ambos conjuntos que contiene todos los elementos contenidos a la vez en A y en B. Si el círculo del conjunto A aparece dentro del círculo de otro B, es que todos los elementos de A también están contenidos en B.
Los '''diagramas de Venn''' son ilustraciones usadas en la rama de la [[Matemática]] y [[Lógica de clases]] conocida como [[teoría de conjuntos]]. Estos diagramas se usan para mostrar gráficamente la agrupación de cosas ''elementos'' en [[conjuntos]], representando cada conjunto mediante un círculo o un óvalo. La posición relativa en el plano de tales círculos muestra la relación entre los conjuntos. Por ejemplo, si los círculos de los conjuntos A y B se solapan, se muestra un área común a ambos conjuntos que contiene todos los elementos contenidos a la vez en A y en B. Si el círculo del conjunto A aparece dentro del círculo de otro B, es que todos los elementos de A también están contenidos en B.


== Orígenes e Historia ==
== Orígenes e Historia ==

Revisión del 17:59 15 jun 2010


Diagrama de Venn mostrando la intersección de dos conjuntos.

Los diagramas de Venn son ilustraciones usadas en la rama de la Matemática y Lógica de clases conocida como teoría de conjuntos. Estos diagramas se usan para mostrar gráficamente la agrupación de cosas elementos en conjuntos, representando cada conjunto mediante un círculo o un óvalo. La posición relativa en el plano de tales círculos muestra la relación entre los conjuntos. Por ejemplo, si los círculos de los conjuntos A y B se solapan, se muestra un área común a ambos conjuntos que contiene todos los elementos contenidos a la vez en A y en B. Si el círculo del conjunto A aparece dentro del círculo de otro B, es que todos los elementos de A también están contenidos en B.

Orígenes e Historia

Ventanal en el comedor del Gonville and Caius College, Cambridge, conmemorando la estancia de Venn y su principal descubrimiento.

Los diagramas de Venn reciben el nombre de su creador, John Venn, matemático y filósofo británico. Estudiante y más tarde profesor en el Caius College de la Universidad de Cambridge, desarrolló toda su producción intelectual entre esas cuatro paredes.

Venn introdujo el sistema de representación que hoy conocemos en julio de 1880 con la publicación de su trabajo titulado « De la representación mecánica y diagramática de proposiciones y razonamientos»[1]​[2]​[3]​en el Philosophical Magazine and Journal of Science, provocando un cierto revuelo en el mundo de la lógica formal. Aunque la primera forma de representación geométrica de silogismos lógicos se atribuye comúnmente a Gottfried Leibniz, y fue luego ampliada por George Boole y Augustus De Morgan, el método de Venn superaba en claridad y sencillez a los sistemas de representación anteriores, hasta el punto de convertirse con el tiempo en un nuevo estándar. Venn fue el primero en formalizar su uso y en ofrecer un mecanismo de generalización para los mismos.

Más adelante desarrolló algo más su nuevo método en su libro Lógica simbólica, publicado en 1881 con el ánimo de interpretar y corregir los trabajos de Boole en el campo de la lógica formal. Aunque no tuvo demasiado éxito en su empeño, su libro se convirtió en una excelente plataforma de ejemplo para el nuevo sistema de representación. Siguió usándolo en su siguiente libro sobre lógica (Los principios de la lógica empírica, publicado en 1889), con lo que los diagramas de Venn fueron a partir de entonces cada vez más empleados como representación de relaciones lógicas.

La primera referencia escrita al término "diagrama de Venn" de la que se tiene constancia es muy tardía (1918), en el libro A Survey of Symbolic Logic, de Clarence Irving Lewis.[4]​[5]​[6]​

Los diagramas de Venn se emplean hoy día para enseñar matemáticas elementales y para reducir la lógica y la Teoría de conjuntos al cálculo simbólico puro. Se suelen usar también en el aula diagramas de Venn de dos o tres conjuntos como herramienta de síntesis, para ayudar a los estudiantes a comparar y contrastar dos o tres de elementos; en este uso, se incluyen dentro de cada elemento las características exclusivas, y en las intersecciones, las comunes con los otros.

Tipos de diagramas de Venn

Diagrama de dos conjuntos

Conjuntos A y B.

Considérese el ejemplo a la derecha: supóngase que el conjunto A (el círculo naranja) representa, por ejemplo, a todas las criaturas vivas con solo dos piernas motrices y que el conjunto B (el círculo azul) contiene a todas las criaturas que pueden volar. El área donde ambos círculos se superponen (que recibe el nombre de intersección entre A y B, o intersección A - B) contendría por tanto todas las criaturas que, al mismo tiempo, pueden volar y tienen sólo dos piernas motrices.

Imaginemos ahora que cada tipo distinto de criatura viva está representado con un punto situado en alguna parte del diagrama. Los humanos y los pingüinos estarían dentro del círculo naranja (el conjunto A) en la parte en la que no se superpone con el círculo azul (el conjunto B), ya que ambos son bípedos y no pueden volar. Los mosquitos, que tienen seis piernas motrices y pueden volar, estarían representados con un punto dentro del círculo azul fuera de la intersección A - B. Los loros, que tienen dos piernas motrices y pueden volar, estarían representados por un punto dentro de la intersección A - B. Cualquier tipo de criatura que ni tuviera dos piernas ni pudiera volar (como por ejemplo las ballenas o las serpientes), estaría representado mediante puntos fuera de ambos círculos.

El diagrama de Venn representado en el ejemplo 1 puede describirse como la relación entre el conjunto A y el conjunto B. El área combinada de ambos conjuntos recibe el nombre de unión de los conjuntos A y B. La unión en este caso contiene todos los tipos de criaturas que tienen dos piernas, pueden volar, o ambas cosas a la vez. El área donde los conjuntos A y B se solapan se define como la intersección de A y B. Contiene todos los tipos de criaturas que pertenecen a la vez a A y a B, es decir, que tienen dos piernas y pueden volar.

Diagrama de Venn mostrando todas las intersecciones posibles entre tres conjuntos A, B y C.

Un diagrama de Venn de dos conjuntos define 4 áreas diferentes (la cuarta es la exterior), que pueden unirse en 6 posibles combinaciones:

  • A (dos patas)
  • B (vuelan)
  • A y B (dos patas y vuelan)
  • A y no B (dos patas y no vuelan)
  • no A y B (más o menos de dos patas, y vuelan)
  • no A y no B (ni tienen dos patas ni vuelan)

A veces se incluye un rectángulo alrededor del diagrama de Venn, que recibe el nombre de universo de discurso (antes se creía en la existencia de un conjunto universal pero Bertrand Russell descubrió que con tal concepto el sistema es inconsistente véase paradoja de Russell). Se usa para representar el conjunto de todas las cosas posibles. La definición del universo, al igual que la de los conjuntos, depende del diagrama sobre el que se representa. La idea de conjunto universal, aunque fue apuntada por el propio Venn, se atribuye habitualmente a Charles Dodgson, más conocido como Lewis Carroll.

Diagramas de tres conjuntos

Los diagramas de tres conjuntos fueron los más corrientes elaborados por Venn en su presentación inicial. Las distintas intersecciones de los tres conjuntos A, B y C definen SIETE áreas diferentes, cuyas posibles uniones suponen 256 combinaciones distintas de los tres conjuntos iniciales.

Más de tres conjuntos

La dificultad de representar más de tres conjuntos mediante diagramas de Venn (o cualquier otra representación gráfica) es evidente. Venn sentía afición a la búsqueda de diagramas para más de tres conjuntos, a los que definía como "figuras simétricas, elegantes en sí mismas". A lo largo de su vida diseñó varias de estas representaciones usando elipses, así como indicaciones para la creación de diagramas con cualquier cantidad de curvas, partiendo del diagrama de tres círculos.

Diagramas de Venn de Edwards

A. W. F. Edwards diseñó representaciones para diagramas de Venn de más de tres conjuntos, proyectando el diagrama sobre una esfera. Se pueden representar fácilmente tres conjuntos tomando tres hemisferios en ángulos rectos (x=0, y=0 y z=0). Un cuarto conjunto se puede representar tomando una curva similar a la juntura de una pelota de tenis que suba y baje alrededor del ecuador. Los conjuntos resultantes pueden proyectarse de nuevo sobre el plano para mostrar diagramas de engranaje, con cantidades cada vez mayores de dientes. Edwards ideó estos diagramas mientras diseñaba la ventana acristalada en memoria de Venn que hoy adorna el comedor de su colegio.

Diagrama para tres conjuntos.
Diagrama para cuatro conjuntos.
Diagrama para cinco conjuntos.
Diagrama para seis conjuntos.

Otros diagramas

Los diagramas de Edwards son topológicamente equivalentes a los diagramas diseñados por Branko Grünbaum, que se basaban en polígonos intersecados, con cantidades crecientes de lados. Phillip Smith ideó diagramas similares de n conjuntos usando curvas senoidales en ecuaciones como y=sin(2ix)/2i, 0 ≤i ≤n-2. Por su parte, Lewis Carroll diseñó un diagrama de cinco conjuntos.

Véanse también: Carta de Smith y Diagrama de Carroll.

Diagramas similares

Diagramas de Euler

Diagrama de Euler.

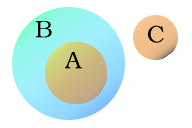
Los diagramas de Euler son similares a los de Venn, pero no necesitan todas las posibles relaciones. Los diagramas de Euler permiten representar inclusión de una clase en otra. Por ejemplo, en el representado a la derecha un conjunto (el A) está totalmente incluido en otro (el B), mientras que otro (el C) no tiene ninguna relación con los dos anteriores.

Los diagramas de Euler anteceden a los diagramas de Venn,[7]​ pero son distintos. Fueron introducidos por Euler para ayudar en la comprensión. John Venn intenta rectificar algunas deficiencias a través de los Diagramas de Venn.

Supongamos que el conjunto A representa todos los tipos de queso que pueden encontrarse en el mundo, y el B representa a todos los comestibles existentes en el mundo. Según el diagrama, se ve claramente que todos los quesos son comestibles, pero no todos los comestibles son quesos. Si definimos el conjunto C como el de las cosas hechas de metal, el diagrama nos permite representar de forma evidente dos afirmaciones adicionales: los comestibles no están hechos de metal, y las cosas hechas de metal no son comestibles.

Diagrama de Johnston

Diagrama de Johnston para la expresión ni A ni B son ciertas.

Los diagramas de Johnston se usan para ilustrar afirmaciones lógicas como ni A ni B son ciertas, y son una forma visual de ilustrar tablas de verdad. Pueden ser idénticos en apariencia a diagramas de Venn, pero no representan conjuntos de elementos.

Mapa de Karnaugh

Artículo principal: Mapa de Karnaugh

Los Mapas de Karnaugh o Diagramas de Veitch son otra forma de representar de forma visual expresiones de álgebra booleana.

Diagrama de Peirce

Los diagramas de Peirce, creados por Charles Peirce, son extensiones de los diagramas de Venn que incluyen información sobre afirmaciones existenciales, disyuntivas, de probabilidades y otras relaciones.[8]​

Referencias

  1. ↑ Venn, John (1880). «On the Diagrammatic and Mechanical Representation of Propositions and Reasonings». The London, Edinburgh, and Dublin Philosophical Magazine and Journal of Science 9 (1-18). 
  2. ↑ Ruskey, Frank y Weston, Mark (2005). «What is a Venn Diagram?». pág. principal: A Survey of Venn Diagrams, The Electronic Journal of Combinatorics. Consultado el agosto 2007. 
  3. ↑ Otte, Andreas (1998). «Venn-Diagramme: Einleitung». Begriffslogik.de. Consultado el agosto 2007. 
  4. ↑ Oxford English Dictionary, 2ª edición.
  5. ↑ Darling, David (-). «Venn Diagram». The Internet Encyclopedia of Science. Consultado el agosto 2007. 
  6. ↑ Bogomolny, Alexander. «Lewis Carroll's Logic Game». Interactive Mathematics Miscellany and Puzzles (en inglés). Consultado el agosto 2007. 
  7. ↑ Euler, Leonard (traducido por Sir David Brewster) (1768, 1823: traducción). Lettres à une Princesse d'Allemagne. San Petersburgo, Edinburgo (traducción):W & C Tait, y Longman et al.  Ver en particular en el vol. 1. las cartas CII - CVIII en las páginas 337-366).
  8. ↑ Ejemplos de diagramas de Peirce

.

Bibliografía

  • Edwards, Anthony W. F. (2004). Cogwheels of the Mind: The Story of Venn Diagrams. Baltimore (Maryland): The John Hopkins University Press. ISBN 0-8018-7434-3. 
  • Stewart, Ian (1992). Another Fine Math You've Got Me Into. Dover Publications. ISBN 0-486-43181-9. 
  • Thompson, Katherine. Cogwheels of the Mind. Reviewed by Katherine Thompson. 

Véase también

Enlaces externos

Herramientas para hacer diagramas de Venn

Herramientas para hacer diagramas de Euler

Obtenido de «https://es.wikipedia.org/w/index.php?title=Diagrama_de_Venn&oldid=38073180»