Diagrama de Schlegel
Apariencia


En geometría, un diagrama de Schlegel es una proyección de un politopo contenido en sobre el espacio a través de un punto que está más allá de una de sus "caras". La entidad resultante es una división politópica de las caras en que es combinatoriamente equivalente al politopo original. En 1886 Victor Schlegel introdujo esta herramienta para estudiar propiedades combinatorias y topológicas de los politopos. En dimensiones, 3 y 4, un diagrama de Schlegel es una proyección de un poliedro sobre el plano dando una figura plana y una proyección de un polícoro al espacio tridimensional, respectivamente. Como tal, los diagramas de Schlegel se usan frecuentemente para visualizar politopos del espacio de cuatro dimensiones.
Ejemplos[editar]
| Dodecaedro | Dodecaplex |
|---|---|
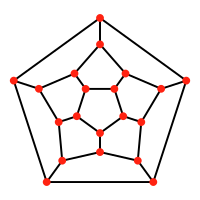 12 caras pentagonales en el plano |
 120 celdas dodecahédricas en el espacio tridimensional |
Referencias[editar]
- Victor Schlegel (1883) Theorie der homogen zusammengesetzten Raumgebilde, Nova Acta, Ksl. Leop.-Carol. Deutsche Akademie der Naturforscher, Band XLIV, Nr. 4, Druck von E. Blochmann & Sohn in Dresden. [1]
- Victor Schlegel (1886) Ueber Projectionsmodelle der regelmässigen vier-dimensionalen Körper, Waren.
- Coxeter, H.S.M.; Regular Polytopes, (Methuen and Co., 1948). (p. 242)
- Regular Polytopes, (3rd edition, 1973), Dover edition, ISBN 0-486-61480-8
- Grünbaum, Branko (2003), Kaibel, Volker; Klee, Victor; Ziegler, Günter M., eds., Convex polytopes (2nd edición), New York & London: Springer-Verlag, ISBN 0-387-00424-6..
Enlaces externos[editar]
 Wikimedia Commons alberga una categoría multimedia sobre Diagrama de Schlegel.
Wikimedia Commons alberga una categoría multimedia sobre Diagrama de Schlegel.- Weisstein, Eric W. «Schlegel graph». En Weisstein, Eric W, ed. MathWorld (en inglés). Wolfram Research.
- Weisstein, Eric W. «Skeleton». En Weisstein, Eric W, ed. MathWorld (en inglés). Wolfram Research.
- George W. Hart: 4D Polytope Projection Models by 3D Printing
- Nrich maths – para estudiantes de secundaria. También útil para profesores.


