Curva cerrada de tipo tiempo

En una variedad Lorentziana de la geometría diferencial, se llama curva cerrada de tipo tiempo o curva temporal cerrada (closed timelike curve, o abreviadamente CTC, en inglés) a la línea de universo de una partícula material que está cerrada en el espacio-tiempo, es decir, que es susceptible de regresar al mismo estado del que partió en el tiempo.

Esta posibilidad fue planteada por Willem Jacob van Stockum en 1937 y por Kurt Gödel en 1949. De probarse la existencia de la CTC, el hecho podría implicar al menos la posibilidad teórica de construir una máquina del tiempo, así como una reformulación de la paradoja del abuelo.

La CTC está relacionada con la deformación gravitatoria y con el cilindro de Tipler, (en referencia al físico Frank J. Tipler), capaces teóricamente de posibilitar el viaje en el tiempo, todo ello contemplado en la relatividad general.

Conos de luz

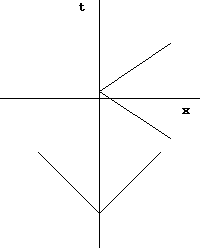
El cono de luz inferior es característico de un espacio-tiempo plano. Todas las coordenadas espacio-temporales incluidas en el cono de luz tienen momentos posteriores. El cono de luz superior no sólo incluye otras ubicaciones temporales simultáneas, no incluye x=0 en momentos futuros, e incluye tiempos anteriores.

Al estudiar la evolución de un sistema según la relatividad general, los físicos se refieren a menudo al cono de luz. Un cono de luz representa cualquier posible evolución de un objeto, dado su concreto estado actual. Las posibles localizaciones del objeto en el futuro se hallan limitadas por la velocidad a que dicho objeto es capaz de moverse, y que, de acuerdo con la teoría de la relatividad, nunca puede superar la velocidad de la luz. Por ejemplo, localizado en una posición $p$ en un momento $t_{0}$ únicamente puede moverse dentro de $c(t_{1}-t_{0})$ en un tiempo $t_{1}$ .

Esta premisa viene representada comúnmente por un gráfico con ubicaciones espaciales a lo largo de un eje horizontal, y temporales a lo largo de un eje vertical, con cifras de t para el tiempo y ct para el espacio. Los conos de luz en esta representación aparecen delimitados por líneas divergentes con una inclinación de 45 grados a partir de la localización puntual del objeto, según la luz viaja en ct a través de t. En tal diagrama, cualquier posible localización futura del objeto descansará dentro del cono de luz, dado que el objeto no puede superar la velocidad de la luz. Por otra parte, toda localización espacial tiene un tiempo futuro, lo que implica que un objeto puede permanecer en cualquier posición en el espacio de forma indefinida.

Todo punto en este diagrama es conocido como evento. Eventos separados se consideran de tipo tiempo (de la expresión inglesa time-like) si están separados unos de otros a lo largo del eje del tiempo, o de tipo espacio (space-like), si se encuentran alineados a lo largo del eje espacial. Si el objeto estuviera en caída libre viajaría por el eje temporal, y si se acelerase, también lo haría en el eje espacial. El rumbo real que toma un objeto a través del espacio-tiempo, en contraposición con aquel que podría tomar, se conoce como línea de universo. Otra definición es que el cono de luz engloba todas las posibles líneas de universo de un objeto.

En las mediciones normales de espacio-tiempo, el cono de luz se orienta siempre hacia delante, lo que se corresponde con la imposibilidad de que un objeto se halle en dos lugares a la vez, o, del mismo modo, que pueda moverse “instantáneamente” a otro lugar. En este tipo de espacio-tiempo, las líneas de universo de los objetos físicos son, por definición, de tipo tiempo. Sin embargo, esta orientación únicamente es cierta en espacio-tiempos 'planos'.

En espacio-tiempos 'curvos' el cono de luz se desviará a lo largo de la línea geodésica del espacio-tiempo. Por ejemplo, al moverse en la proximidad de una estrella, la gravedad de la misma tirará del objeto afectando a su línea de universo, de manera que sus posibles posiciones futuras se aproximarán igualmente a la estrella. Esto aparecerá como un cono de luz ligeramente curvado en el diagrama correspondiente. Todo objeto en caída libre en estas circunstancias continuará moviéndose a lo largo del eje temporal t, pero a un observador externo le parecerá que se acelera en el espacio en la misma medida; una situación normal, dado el caso de que el objeto se encuentre en órbita.

En casos más extremos de espacio-tiempos con elevada curvatura gravitacional, el cono de luz se curvará fuera de esa delimitación de 45 grados, lo que significa que hay potenciales posiciones futuras, desde el marco de referencia del objeto, que están separadas espacialmente de un observatorio en reposo.

Desde este punto de vista exterior, el objeto puede desplazarse “instantáneamente” a través del espacio. En tales situaciones el objeto tendría que haberse movido, ya que su actual ubicación espacial no estaría encerrada en su propio cono de luz futuro. Por otra parte, con una atracción gravitatoria suficiente, hay localizaciones de eventos que están en el "pasado", observadas desde el exterior. Con un movimiento conveniente de lo que parece su propio eje espacial, el objeto, observado desde fuera, semeja viajar en el tiempo.

Una curva cerrada de tipo tiempo puede ser creada si se establece una serie de conos de luz que formen un bucle hacia atrás sobre sí mismos, de manera que sea posible para un objeto moverse a través de ese bucle y volver al mismo sitio y tiempo desde el que partió. Las órbitas alrededor de objetos de alta densidad que ejercen en torno a sí intensa fuerza gravitatoria son un ejemplo de tal clase de bucles cerrados. Un objeto atrapado en una órbita semejante regresaría repetidamente al mismo punto del espacio-tiempo si se hallase en caída libre. La vuelta a la ubicación espacio-temporal original sería contemplada sólo como posibilidad; el cono de luz futuro del objeto incluiría puntos espaciotemporales que se mostrarían capaces de moverse adelante y atrás en el tiempo, facilitando, bajo tales condiciones, al objeto el efectuar un viaje en el tiempo. Este precisamente es el mecanismo de que se serviría el cilindro de Tipler (Frank J. Tipler) para funcionar como máquina del tiempo.

Relatividad general

Las CTC suelen aparecer en inobjetables soluciones exactas de la ecuación de campo de Einstein, dentro de la relatividad general, incluidas algunas de sus soluciones más importantes:

El agujero negro de Kerr (que describe la física de un agujero negro en rotación).
Relacionado con el anterior, el interior de un agujero negro de tipo BTZ puede posibilitar igualmente la CTC.
La solución de Willem Jacob van Stockum (con una configuración de materia, o dust, rotatoria simétrica).
La solución del universo rotatorio de Gödel, la verosimilitud de la cual en su momento provocó en Einstein serias dudas sobre su propia teoría.
J. Richard Gott asimismo ha propuesto un mecanismo para crear curvas temporales cerradas usando cuerdas cósmicas.
El Espacio de Misner, un modelo matemático abstracto de espacio-tiempo descubierto por Charles Misner, de la University of Maryland. También es conocido como orbifold Lorentziana ( $\mathbb {R} ^{1,1}/boost$ ).
La solución de Bonnor-Steadman describe situaciones de laboratorio mediante bolas en rotación.
Ronald Mallett propone usar un giroscopio láser de anillo para crear la CTC, al considerar los campos gravitacionales fuertes y débiles producidos por una simple y continua circulación unidireccional de un haz de luz. Argumenta que con energía suficiente, el láser circulante podría producir no sólo arrastre de marco sino curvas cerradas de tipo tiempo.

Algunos de estos ejemplos son, como el cilindro de Tipler, más bien artificiales, pero, a juzgar por su aspecto externo, la solución de Kerr se piensa que puede ser válida. En el resto, la mayoría de los físicos opina que las soluciones son indemostrables.

Consecuencias

Un rasgo de las curvas cerradas de tipo tiempo es que abren la posibilidad de una línea de universo que no esté conectada a tiempos anteriores, y así de la existencia de eventos que puedan no ser debidos a una causa anterior a ellos mismos. Ordinariamente, la causalidad exige que cada evento en el espacio-tiempo sea producido por su causa, en todo marco de referencia en reposo. Este principio es crítico en el determinismo, el cual, en el lenguaje de la relatividad general, establece que a partir de un conocimiento completo del universo en una superficie de Cauchy de tipo espacio es posible determinar o “predecir” cualquier estado posterior del espacio-tiempo.

Sin embargo, en una CTC, la causalidad se rompe porque un evento puede ser simultáneo con su causa, de modo que el evento en realidad se convierte en su propia causa. Basados sólo en el conocimiento del pasado, es imposible determinar si algo existe en la CTC que pueda interferir con otros objetos en el espacio-tiempo. Una curva cerrada de tipo tiempo, por consiguiente, resulta en un horizonte de Cauchy, y una región de espacio-tiempo que no puede ser predicha a partir de un conocimiento perfecto de algún momento pasado.

La existencia de CTC impone restricciones a los estados de campos de materia-energía que permite la física. Si propagamos la configuración de un campo a lo largo de una familia de líneas de universo cerradas de tipo tiempo, debemos obtener un estado que es idéntico al original. Este es el enfoque que ha sido propuesto por algunos científicos para descartar la existencia de curvas cerradas de tipo tiempo.

Véase también

Referencias

S. Carroll (2004). Spacetime and Geometry. Addison Wesley. ISBN 0-8053-8732-3.
Kurt Gödel (1949). «An Example of a New Type of Cosmological Solution of Einstein's Field Equations of Gravitation». Rev. Mod. Phys. 21: 447.

Enlaces externos en inglés

A Primer on Time Travel-(backup in the Internet Archive)

Datos: Q1876815