Validación cruzada
La validación cruzada o cross-validation es una técnica utilizada para evaluar los resultados de un análisis estadístico y garantizar que son independientes de la partición entre datos de entrenamiento y prueba. Consiste en repetir y calcular la media aritmética obtenida de las medidas de evaluación sobre diferentes particiones. Se utiliza en entornos donde el objetivo principal es la predicción y se quiere estimar la precisión de un modelo que se llevará a cabo a la práctica.[1] Es una técnica muy utilizada en proyectos de inteligencia artificial para validar modelos generados.

Contexto[editar]
La validación cruzada proviene de la mejora del método de retención o holdout method. Este consiste en dividir en dos conjuntos complementarios los datos de muestra, realizar el análisis de un subconjunto (denominado datos de entrenamiento o training set), y validar el análisis en el otro subconjunto (denominado datos de prueba o test set), de forma que la función de aproximación sólo se ajusta con el conjunto de datos de entrenamiento y a partir de aquí calcula los valores de salida para el conjunto de datos de prueba (valores que no ha analizado antes). La ventaja de este método es que es muy rápido a la hora de computar. Sin embargo, este método no es demasiado preciso debido a la variación de resultados obtenidos para diferentes datos de entrenamiento. La evaluación puede depender en gran medida de cómo es la división entre datos de entrenamiento y de prueba, y por lo tanto puede ser significativamente diferente en función de cómo se realice esta división. Debido a estas carencias aparece el concepto de validación cruzada.[3]

Objetivo de la validación cruzada[editar]
Suponemos que tenemos un modelo con uno o más parámetros de ajuste desconocidos y unos datos de entrenamiento que queremos analizar. El proceso de ajuste optimiza los parámetros del modelo para que éste se ajuste a los datos de entrenamiento tan bien como pueda. Si tomamos una muestra independiente como dato de prueba (validación), del mismo grupo que los datos de entrenamiento, normalmente el modelo no se ajustará a los datos de prueba igual de bien que a los datos de entrenamiento. Esto se denomina sobreajuste y acostumbra a pasar cuando el tamaño de los datos de entrenamiento es pequeño o cuando el número de parámetros del modelo es grande. La validación cruzada es una manera de predecir el ajuste de un modelo a un hipotético conjunto de datos de prueba cuando no disponemos del conjunto explícito de datos de prueba.[4]
Tipos de validaciones cruzadas[editar]
Validación cruzada de K iteraciones[editar]
En la validación cruzada de K iteraciones o K-fold cross-validation los datos de muestra se dividen en K subconjuntos. Uno de los subconjuntos se utiliza como datos de prueba y el resto (K-1) como datos de entrenamiento. El proceso de validación cruzada es repetido durante k iteraciones, con cada uno de los posibles subconjuntos de datos de prueba. Finalmente se realiza la media aritmética de los resultados de cada iteración para obtener un único resultado. Este método es muy preciso puesto que evaluamos a partir de K combinaciones de datos de entrenamiento y de prueba, pero aun así tiene una desventaja, y es que, a diferencia del método de retención, es lento desde el punto de vista computacional. En la práctica, la elección del número de iteraciones depende de la medida del conjunto de datos. Lo más común es utilizar la validación cruzada de 10 iteraciones (10-fold cross-validation).[5][4]

Validación cruzada aleatoria[editar]
Este método consiste al dividir aleatoriamente el conjunto de datos de entrenamiento y el conjunto de datos de prueba. Para cada división la función de aproximación se ajusta a partir de los datos de entrenamiento y calcula los valores de salida para el conjunto de datos de prueba. El resultado final se corresponde a la media aritmética de los valores obtenidos para las diferentes divisiones. La ventaja de este método es que la división de datos entrenamiento-prueba no depende del número de iteraciones. Pero, en cambio, con este método hay algunas muestras que quedan sin evaluar y otras que se evalúan más de una vez, es decir, los subconjuntos de prueba y entrenamiento se pueden solapar.[6]

Validación cruzada dejando uno fuera[editar]
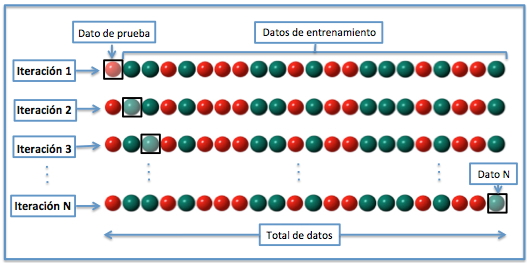
La validación cruzada dejando uno fuera o Leave-one-out cross-validation (LOOCV) implica separar los datos de forma que para cada iteración tengamos una sola muestra para los datos de prueba y todo el resto conformando los datos de entrenamiento. La evaluación viene dada por el error, y en este tipo de validación cruzada el error es muy bajo, pero en cambio, a nivel computacional es muy costoso, puesto que se tienen que realizar un elevado número de iteraciones, tantas como N muestras tengamos y para cada una analizar los datos tanto de entrenamiento como de prueba. [7]
Cálculo del error[editar]
La evaluación de las diferentes validaciones cruzadas normalmente viene dada por el error obtenido en cada iteración, ahora bien, por cada uno de los métodos puede variar el número de iteraciones, según la elección del diseñador en función del número de datos total.[8]
Error de la validación cruzada de K iteraciones[editar]
En cada una de las k iteraciones de este tipo de validación se realiza un cálculo de error. El resultado final lo obtenemos a partir de realizar la media aritmética de los K valores de errores obtenidos, según la fórmula:
Es decir, se realiza el sumatorio de los K valores de error y se divide entre el valor de K.
Error de la validación cruzada aleatoria[editar]
En la validación cruzada aleatoria a diferencia del método anterior, cogemos muestras al azar durante k iteraciones, aunque de igual manera, se realiza un cálculo de error para cada iteración. El resultado final también lo obtenemos a partir de realizar la media aritmética de los K valores de errores obtenidos, según la misma fórmula:
Error de la validación cruzada dejando uno fuera[editar]
En la validación cruzada dejando uno fuera se realizan tantas iteraciones como muestras (N) tenga el conjunto de datos. De forma que para cada una de las N iteraciones se realiza un cálculo de error. El resultado final lo obtenemos realizando la media aritmética de los N valores de errores obtenidos, según la fórmula:
Donde se realiza el sumatorio de los N valores de error y se divide entre el valor de N.
Medidas de ajuste[editar]
El objetivo de la validación cruzada consiste en estimar el nivel de ajuste de un modelo a un cierto conjunto de datos de prueba independientes de las utilizadas para entrenar el modelo. Estas medidas obtenidas pueden ser utilizadas para estimar cualquier medida cuantitativa de ajuste apropiada para los datos y el modelo. Por ejemplo, en un modelo basado en clasificación binaria, cada muestra se prevé como correcta o incorrecta (si pertenece a la temática o no), de forma que en este caso, se puede usar la 'tasa de error de clasificación' para resumir el ajuste del modelo. Así mismo, se podrían utilizar otras medidas como el valor predictivo positivo. Cuando el valor a predecir se distribuye de forma continua se puede calcular el error utilizando medidas como: el error cuadrático medio, la desviación de la media cuadrada o la desviación absoluta media.
Ejemplos de aplicación[editar]
La validación cruzada se puede utilizar para comparar los resultados de diferentes procedimientos de clasificación predictiva. Por ejemplo, supongamos que tenemos un detector que nos determina si una cara pertenece a una mujer o a un hombre y consideramos que han sido utilizados dos métodos diferentes, por ejemplo, máquinas de vectores de soporte (SVM) y K-vecinos más cercanos (Knn), ya que ambos nos permiten clasificar las imágenes. Con la validación cruzada podríamos comparar los dos procedimientos y determinar cuál de los dos es el más preciso. Esta información nos la proporciona la tasa de error que obtenemos al aplicar la validación cruzada por cada uno de los métodos planteados.
La validación cruzada de "k" iteraciones (k-fold cross validation) nos permite evaluar también modelos en los que se utilizan varios clasificadores. Continuando con el ejemplo anterior, si tenemos un detector que nos determina si en una imagen aparece un hombre o una mujer, y éste utiliza cuatro clasificadores binarios para detectarlo, también podemos utilizar la validación cruzada para evaluar su precisión. Si tenemos un total de 20 datos (imágenes), y utilizamos el método 4-fold cross validation, se llevarán a cabo cuatro iteraciones, y en cada una se utilizarán unos datos de entrenamiento diferentes, que serán analizadas por cuatro clasificadores, que posteriormente evaluarán los datos de prueba. De este modo por cada muestra obtendremos cuatro resultados, y si hacemos la media entre los resultados de cada clasificador y entre las cuatro iteraciones realizadas, obtendremos el valor resultante final.

Cuestiones computacionales[editar]
La mayoría de las formas de validación cruzada son fáciles de implementar, siempre y cuando una implementación del método de predicción objeto de estudio esté disponible. En particular, el método de predicción sólo necesitan estar disponibles como una "caja negra" no hay necesidad de tener acceso a las partes internas de su aplicación. Si el método de predicción es costoso de entrenar, la validación cruzada puede ser muy lenta ya que el entrenamiento deberá llevarse a cabo en varias ocasiones.
En algunos casos como el de mínimos cuadrados o regresión kernel (del núcleo), la validación cruzada se puede acelerar de manera significativa por el pre-cálculo de ciertos valores que son necesarios en varias ocasiones en el entrenamiento, o mediante el uso rápido "reglas de actualización" como la fórmula de Sherman-Morrison. Sin embargo hay que tener cuidado para preservar completamente el conjunto de validación del procedimiento de entrenamiento, de lo contrario se puede dar lugar a un sesgo.
Un ejemplo extremo de la aceleración de la validación cruzada se produce en la regresión lineal, donde los resultados de la validación cruzada son expresiones de forma cerrada conocidas como suma de cuadrados del error de predicción residual (PRENSS).
Limitaciones y uso no adecuado[editar]
La validación cruzada sólo produce resultados significativos si el conjunto de validación y prueba se han extraído de la misma población. En muchas aplicaciones de modelado predictivo, la estructura del sistema que está siendo estudiado evoluciona con el tiempo. Esto puede introducir diferencias sistemáticas entre los conjuntos de entrenamiento y validación. Por ejemplo, si un modelo para predecir el valor de las acciones está entrenado con los datos de un período de cinco años determinado, no es realista para tratar el siguiente período de cinco años como predictor de la misma población.
Otro ejemplo, supongamos que se desarrolla un modelo para predecir el riesgo de un individuo para ser diagnosticado con una enfermedad en particular en el próximo año. Si el modelo se entrena con datos de un estudio que sólo afecten a un grupo poblacional específico (por ejemplo, solo jóvenes o solo hombres varones), pero se aplica luego a la población en general, los resultados de la validación cruzada del conjunto de entrenamiento podrían diferir en gran medida de la clasificación real.
Si se lleva a cabo correctamente, y si el conjunto de validación y de conjunto de entrenamiento son de la misma población, la validación cruzada es casi imparcial. Sin embargo, hay muchas maneras en que la validación cruzada puede ser mal utilizada. Si se abusa y posteriormente se lleva a cabo un estudio real de validación, es probable que los errores de predicción en la validación real sean mucho peores de lo esperado sobre la base de los resultados de la validación cruzada.
Estas son algunas formas en que la validación cruzada puede ser mal utilizada:
- Mediante el uso de la validación cruzada para evaluar varios modelos, y sólo indicando los resultados para el modelo con los mejores resultados.
- Al realizar un análisis inicial para identificar las características más informativas utilizando el conjunto de datos completo, si la selección de característica o el ajuste del modelo lo requiere por el propio procedimiento de modelado, esto debe repetirse en cada conjunto de entrenamiento. Si se utiliza la validación cruzada para decidir qué características se van a utilizar, se deberá realizar un proceso interno de validación cruzada para llevar a cabo la selección de características en cada conjunto de entrenamiento.
- Al permitir que algunos de los datos de entrenamiento esté también incluido en el conjunto de prueba, esto puede suceder debido a "hermanamiento" en el conjunto de datos, con lo que varias muestras exactamente idénticas o casi idénticas pueden estar presentes en el conjunto de datos.
Véase también[editar]
- Doble ciego
- Inteligencia artificial
- Aprendizaje automático
- Aprendizaje supervisado
- Máquinas de vectores de soporte
- K-vecinos más cercanos
- Regresión lineal
Enlaces externos[editar]
- Smarter-than-you machines, creado por V.V.V. (En inglés)
- Scientists worry machines may outsmart man, creado por John Markoff (En inglés)
- Inteligencia artificial. El hombre y las máquinas pensantes, creado por Edith Delgado (En castellano)
- The man-machine and artificial intelligence Archivado el 7 de junio de 2007 en Wayback Machine., creado por Bruce Mazlish. Ideas del año 1995. (En inglés)
- The concept of k-fold cross-validation. (En inglés)
Referencias[editar]
- ↑ Devijver, P. A., and J. Kittler, Pattern Recognition: A Statistical Approach, Prentice-Hall, Londres, 1982
- ↑ Jean-Philippe Lang, Predictors tutorial Archivado el 3 de enero de 2014 en Wayback Machine., Bioinformatic Department Projects
- ↑ Jeff Schneider, The holdout method, The school of computer science, 7 de febrero de 1997
- ↑ a b Payam Refaeilzadeh, Lei Tang, Huan Lui, k-fold Cross-Validation, Arizona State University, 6 de noviembre de 2008
- ↑ FH Joanneum, Cross-Validation Explained, Institute for Genomics and Bioinformatics, 2005-2006
- ↑ Andrew W. Moore, Cross-validation for detecting and preventing overfitting Archivado el 10 de agosto de 2011 en Wayback Machine., Carnegie Mellon University
- ↑ Charles Elkan, Evaluating Classifiers University of California, San Diego, 18 de enero de 2011
- ↑ Ricardo Gutiérrez-Osuna,Leave-one-out Cross Validation Archivado el 2 de diciembre de 2012 en Wayback Machine. Wright State University


