Punto del infinito

El punto del infinito, punto en el infinito o punto impropio es una entidad topológica y geométrica que se introduce a modo de cierre o frontera infinita del conjunto de los números reales. Cuando se añade a la recta real genera una curva cerrada (véase fig.1) conocida como recta proyectiva real, , que no es equivalente a la recta real ampliada, que tiene dos puntos distintos en el infinito. Esta condición se expresa de la forma siguiente:
En el caso del plano afín (incluido el espacio bidimensional), hay un punto ideal para cada haz de paralelas del plano. La unión de estos puntos produce un plano proyectivo, en el que no se puede distinguir ningún punto, si se "olvida" qué puntos se agregaron. Esto es válido para una geometría sobre cualquier cuerpo y, de manera más general, sobre cualquier anillo de división.[1]
Topología T de compactificación
[editar]Para que el punto en el infinito represente efectivamente el infinito real se define en la topología formada por todos los conjuntos:
- A, que son abiertos de
- B, que son complementarios de conjuntos compactos (cerrados y acotados por el teorema de Heine-Borel) de .
Los conjuntos A son los abiertos de que no contienen el : mientras que los conjuntos B son los que sí lo contienen.
Sea una sucesión de números reales tales que . Dentro del conjunto de los números reales, esto quiere decir únicamente que:
Pero esta misma condición implica en que
Es decir, que en se escribe también . Sin embargo, sólo en se puede decir que la sucesión converge, puesto que .
Con este proceso hemos conseguido "compactificar" ya que toda sucesión en tiene una parcial convergente (las que no lo cumplían, las no acotadas, ahora sí lo cumplen). Lo que hemos hecho es un caso particular de una construcción topológica más general: la compactificación de Alexándrov, que consiste en tomar un espacio y añadirle un punto (comúnmente llamado del infinito por analogía) de forma que el espacio resultante sea compacto. Esto no funciona para cualquier espacio; hace falta que el espacio cumpla ciertas condiciones necesarias: ser de Hausdorff y localmente compacto. Véase Compactificación de Alexándrov para el caso general.
En el plano complejo
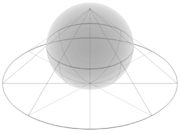
[editar]El punto del infinito también puede añadirse al plano complejo, , de manera que se transforme en una superficie cerrada (véase fig.cp1 y fig.cp2), la recta proyectiva compleja, , también llamada esfera de Riemann, una esfera sobre el plano complejo y desde cuyo polo superior se proyectan el resto de puntos de la esfera sobre el plano complejo. De este modo, se establece una biyección en la que a cada punto de la esfera le corresponde uno del plano complejo. El homólogo del punto desde el que proyectamos estereográficamente se convierte en el punto del infinito.
Rectas paralelas en ℝ2
[editar]Al igual que dos rectas secantes comparten un punto, dos rectas paralelas comparten una dirección, por lo que a esas direcciones también se las conoce como puntos impropios de esas rectas en las que se encuentran. Por ejemplo, en no es posible determinar con exactitud la posición del punto del infinito mediante unas coordenadas absolutas . Para conseguirlo, se acude a las coordenadas homogéneas , donde e representan la dirección del vector director de la recta. Las anteriores coordenadas absolutas vienen dadas por:
El punto podría representarse, por ejemplo, como o como . La representación del punto del infinito se obtiene igualando , así:
El punto del infinito del eje OX sería el , el , etc.
Ahora cualquier par de rectas se cortan, ya sea porque fueran secantes de partida o porque eran paralelas y por tanto comparten punto del infinito. Esta es la idea básica a partir de la que se construye la geometría proyectiva.
Véase también
[editar]- Coordenadas homogéneas
- Esfera de Riemann
- Compactación de Alexándrov
- Línea del horizonte
- Punto de fuga
Referencias
[editar]- ↑ Weisstein, Eric W. «Point at Infinity». mathworld.wolfram.com (en inglés). Wolfram Research. Consultado el 28 de diciembre de 2016.










![{\displaystyle \forall K>0\ \exists m\in \mathbb {N} |{\text{ si }}n>m\Rightarrow x_{n}\notin [-K,K]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/1fb9b4bc47c7d288c521ffdf4f0c804695f556c0)