Método por agotamiento
El método por agotamiento[1] es un procedimiento geométrico de aproximación a un resultado, con el cual el grado de precisión aumenta en la medida en que avanza el cálculo. Fue creado por Eudoxo de Cnido, reconocido por su teoría de las proporciones y teoremas sobre ella.
También se conoce como:
Historia[editar]
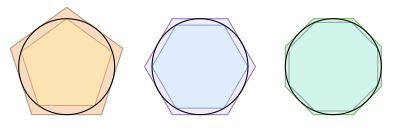
El sofista Antifonte (430 a. C.) trató de determinar el área del círculo inscribiendo en él un mayor número de triángulos, cada vez más pequeños, hasta que su área se colmara.
Un ejemplo más famoso del método exhaustivo o por agotamiento es el del cálculo de la longitud de una circunferencia efectuado por Arquímedes. Él utilizó dos métodos:
- el método de agotamiento, inscribiendo polígonos regulares en una circunferencia de radio unitario, y
- el método de compresión, circunscribiendo polígonos a la circunferencia. De este modo, al aumentar el número de lados de los polígonos, las figuras tenderán a acercarse a la forma de la circunferencia, tanto que Arquímedes pudo obtener una medida bastante precisa del número π.
El método de agotamiento está descrito en el Método, un libro de Arquímedes en el que se explica este procedimiento es la base de los conceptos que en el siglo XVII permitieron a Isaac Newton y a Leibniz unificar el cálculo diferencial con el integral, lo cual conllevó la posterior definición rigurosa de límite de una función por Bernard Bolzano, Cauchy y Weierstrass.
El método de agotamiento es el precursor del concepto de Suma de Riemann que permite definir con rigor la integral de una función en un intervalo.
Referencias[editar]
- ↑ Alberto Rodríguez de Rivera Meneses: «Arquímedes. El genio de Siracusa», artículo en Historia de las Matemáticas, en el sitio web de la Universidad Autónoma de Madrid.
- ↑ Charla mantenida por el Dr. Ing. Carlos P. Filipich en la Academia de Ingeniería de la Provincia de Buenos Aires con motivo de su incorporación como académico correspondiente Archivado el 4 de marzo de 2016 en Wayback Machine., artículo del 18 de mayo de 2011 en el sitio web de la AcaIngPBA.
«De Eudoxio destacamos dos líneas que serán básicas para la tarea de Arquímedes: las proporciones geométricas y el método exhaustivo o por agotamiento». - ↑ Zúñiga, Angel Ruiz (1997). Elementos de Cálculo Diferencial : Historia Y Ejercicios Resueltos. Editorial Universidad de Costa Rica. ISBN 978-9977-67-439-1. Consultado el 16 de julio de 2022.
- ↑ «El método de exhaución.». descartes.cnice.mec.es. Consultado el 16 de julio de 2022.
