Intervalo (música)

Recibe el nombre de quinta porque hay una distancia de cinco grados entre las notas que lo forman (do y sol)
Recibe el apelativo de justa porque hay una distancia de tres tonos y un semitono entre los sonidos que lo forman.
Un intervalo es el acercamiento (en términos de altura) entre dos notas musicales o entre dos sonidos. En general, suelen medirse según las notas de una escala incluyendo los extremos (por ejemplo, entre RE y FA, si se cuenta de manera ascendente, hay una tercera), o bien por la diferencia de tonos y semitonos, o solamente de semitonos. Por ejemplo, una quinta justa es un intervalo de 7 semitonos que se miden en un teclado.
Tipos de intervalos[editar]
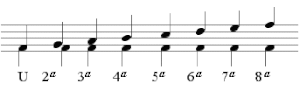
Los intervalos tonales (a veces llamados consonancias perfectas) pueden ser justos; los modales (a veces llamados consonancias imperfectas y disonancias) pueden ser mayores o menores. Además, todos los tipos de intervalos pueden ser aumentados o disminuidos (incluyendo la segunda que sí puede disminuirse).[cita requerida]
Se denomina armónico al intervalo cuyos sonidos suenan simultáneamente, y melódico a aquel cuyos sonidos suenan sucesivamente.[cita requerida]
Los intervalos melódicos pueden ser, además, ascendentes o descendentes.[cita requerida]
Se consideran simples los que no son mayores que una octava y compuestos los que la exceden. Los intervalos compuestos son análogos a los intervalos simples correspondientes. Así, una novena es una segunda a la octava y puede ser mayor o menor; una duodécima es análoga a una quinta y puede ser justa, aumentada o disminuida.[cita requerida]
Se llaman complementarios los intervalos que, sumados, conforman una octava: una cuarta y una quinta son complementarias. Nótese que la suma de los cuatro grados de la cuarta y los cinco grados de la quinta se resuelve en ocho grados, no en nueve, porque el cuarto grado de la cuarta es a la vez el tercer grado de la quinta.[cita requerida]
Denominación de los intervalos simples[editar]
| Nombre del intervalo/Grados[1] | Distancia en tonos y semitonos | Como suena en el sistema temperado |
|---|---|---|
| Unísono[2] | Mismo sonido | |
| Segunda menor | 1 semitono | ⓘ |
| Segunda mayor o tercera disminuida | 1 tono | ⓘ |
| Tercera menor o segunda aumentada | 1 1/2 tonos | |
| Tercera mayor o cuarta disminuida | 2 tonos | |
| Cuarta justa o tercera aumentada | 2 1/2 tonos | |
| Cuarta aumentada o quinta disminuida (llamada tritono)[3] | 3 tonos | ⓘ
|
| Quinta justa o sexta disminuida | 3 1/2 tonos | ⓘ |
| Sexta menor o quinta aumentada | 4 tonos | ⓘ |
| Sexta mayor o séptima disminuida | 4 1/2 tonos | ⓘ |
| Séptima menor o sexta aumentada | 5 tonos | ⓘ |
| Séptima mayor | 5 1/2 tonos | ⓘ
|
| Octava justa | 6 tonos | ⓘ |

U = unísono (dos notas iguales)
m2 = de segunda menor (1st)
M2 = de segunda mayor (1T)
m3 = de tercera menor (1T 1st)
M3 = de tercera mayor (2T)
P4 = de cuarta justa o perfecta (2T 1st)
TT = de cuarta aumentada o tritono (2T 2st)
P5 = de quinta justa o perfecta (3T 1st)
m6 = de sexta menor (3T 2st)
M6 = de sexta mayor (4T 1st)
m7 = de séptima menor (4T 2st)
M7 = de séptima mayor (5T 1st)
P8 = de octava justa o perfecta (5T 2st)
Con la segunda nota en la siguiente octava y manteniendo la fundamental se generan los intervalos de novena, que equivale con una octava de diferencia al de segunda, el de undécima, que equivale al de cuarta, el de treceava, que equivale al de sexta, etc.
Con la segunda nota en la siguiente octava y manteniendo la fundamental se generan los intervalos de novena, que equivale con una octava de diferencia al de segunda, el de undécima, que equivale al de cuarta, el de treceava, que equivale al de sexta, etc. ⓘ ⓘ
EJEMPLO
2m desde C = Db
4J desde A = D
7M desde F = E
Intervalos formados por los mismos sonidos[editar]
Puede ocurrir que dos intervalos formados por dos parejas iguales de sonidos tengan distinto nombre dependiendo de su función y del contexto musical en el que se encuentren.
| Intervalo | 1/2 | 1 | 1-1/2 | 2 | 2-1/2 | 3 | 3-1/2 | 4 | 4-1/2 | 5 | 5-1/2 | 6 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 2ª | 2m | 2M | 2A | |||||||||
| 3ª | 3d | 3m | 3M | 3A | ||||||||
| 4ª | 4d | 4J | 4A | |||||||||
| 5ª | 5d | 5J | 5A | |||||||||
| 6ª | 6d | 6m | 6M | 6A | ||||||||
| 7ª | 7d | 7m | 7M | 7A | ||||||||
| 8ª | 8d | 8J |
- Horizontalmente se indica la distancia entre los sonidos.
- Verticalmente se indican los intervalos.
Historia[editar]
Los primeros trabajos teóricos conocidos son los de Aristóxeno de Tarento, quien se basó en un método tanto empírico como matemático, a diferencia de las especulaciones filosóficas y matemáticas de Pitágoras.
Antiguamente se empleaba para su enseñanza un instrumento llamado monocordio. El cálculo matemático de las frecuencias de los sonidos e intervalos musicales fue estudiado en el siglo XVI por Simon Stevin mediante funciones exponenciales. Durante el siglo XVII, los investigadores Francesco Cavalieri y Juan Caramuel aplicaron el cálculo logarítmico.
En el siglo XIX, Hermann Helmholtz construyó los resonadores que hoy llevan su nombre, posteriormente utilizados para demostrar que todos los sonidos son por naturaleza complejos y consisten en una serie de sonidos concomitantes o armónicos naturales en intervalos que son iguales a los demostrados por el monocordio.
Consonancia y disonancia[editar]
La calificación de intervalos como consonantes o disonantes ha variado enormemente a lo largo de los siglos, así como la definición de lo consonante o disonante en sí.
Por ejemplo, durante la Edad Media la autoridad adjudicada a Pitágoras llevó a los especuladores a considerar a la cuarta justa como la consonancia perfecta y a utilizarla para la composición de organa. Durante la misma época, especulaciones de carácter teológico llevaron a considerar a la cuarta aumentada, llamada "tritono", como diabólica (tritonus diabolus in musica est).
La armonía tradicional desde el siglo XVII considera disonantes los intervalos armónicos de primera aumentada —semitono cromático—, segunda mayor o menor, cuarta aumentada, quinta disminuida o aumentada, séptima mayor o menor y octava disminuida o aumentada. Una posible consideración más detallada es la siguiente:
- Consonancias perfectas: los intervalos de 4ª, 5ª y 8ª cuando son justas.
- Consonancias imperfectas: los intervalos de 3ª y 6ª cuando son mayores o menores.
- Disonancias absolutas: los intervalos de 2ª y 7ª mayores y menores.
- Disonancias condicionales: todos los intervalos aumentados y disminuidos, excepto la 4ª aumentada y la 5ª disminuida.
- Semiconsonancias: la 4ª aumentada y la 5ª disminuida.
Además, en el contexto de la armonía tradicional, el intervalo melódico de cuarta aumentada es considerado disonante.
Frecuencias[editar]
La diferencia de la frecuencia entre las dos notas de un intervalo se puede medir mediante la relación entre ambas frecuencias. En algunas afinaciones se utilizan ciertos intervalos justos, es decir que corresponden a fracciones simples, por ejemplo 2:1 (octava), 3:2 (quinta justa), 4:3 (cuarta justa), 5:3 (sexta mayor), 5:4 (tercera mayor), 6:5 (tercera menor) y 8:5 (sexta menor).
Intervalos armónicos o melódicos[editar]
Un intervalo se puede producir tocando ambas notas al mismo tiempo (intervalo armónico), o una después de otra (intervalo melódico). En este último caso se puede diferenciar la dirección del sonido entre ascendente (cuando la segunda nota es más aguda que la primera) y descendente (cuando la segunda nota es más grave que la primera).
Clasificación[editar]
Los intervalos pueden describirse, clasificarse o compararse entre sí según diversos criterios.
Melódico y armónico[editar]
Un intervalo puede describirse como
- Vertical o armónico si las dos notas suenan simultáneamente
- Horizontal, lineal o melódico si suenan sucesivamente.[4] Los intervalos melódicos pueden ser ascendentes (el tono más grave precede al más agudo) o descendentes.
Diatónico y cromático[editar]
En general,
- Un intervalo diatónico es un intervalo formado por dos notas de una escala diatónica.
- Un intervalo cromático es un intervalo no diatónico formado por dos notas de una escala cromática.

En la escala diatónica de Do mayor hay 14 intervalos diatónicos y 10 cromáticos (Ascendentes y descendentes, sin contar el intervalo Unísono).[5]
La tabla arriba representa los 56 intervalos diatónicos formados por las notas de la escala de Do mayor (una escala diatónica). Observa que estos intervalos, así como cualquier otro intervalo diatónico, también pueden estar formados por las notas de una escala cromática.
La distinción entre intervalos diatónicos y cromáticos es controvertida, ya que se basa en la definición de escala diatónica, que es variable en la literatura. Por ejemplo, el intervalo Si-E♭ (una cuarta disminuida, que aparece en la escala armónica de Do menor) se considera diatónico si las escalas armónicas menores también se consideran diatónicas.[6] En caso contrario, se considera cromática. Para más detalles, véase el artículo principal.
Según una definición comúnmente utilizada de escala diatónica[7] (que excluye las escalas menor armónica y menor melódica), todos los intervalos perfectos, mayores y menores son diatónicos. Por el contrario, ningún intervalo aumentado o disminuido es diatónico, excepto la cuarta aumentada y la quinta disminuida.

La distinción entre intervalos diatónicos y cromáticos también puede ser sensible al contexto. Los mencionados 56 intervalos formados por la escala de Do mayor se denominan a veces diatónicos de Do mayor. Todos los demás intervalos se denominan cromáticos de Do mayor. Por ejemplo, la quinta perfecta A♭-E♭ es cromática para Do mayor, porque A♭ y E♭ no están contenidos en la escala de Do mayor. Sin embargo, es diatónica respecto a otras, como la escala de La mayor.
Consonante y disonante[editar]
Consonancia y disonancia son términos relativos que se refieren a la estabilidad, o estado de reposo, de determinados efectos musicales. Los intervalos disonantes son aquellos que causan tensión y desean ser resueltos a intervalos consonantes.
Estos términos son relativos al uso de diferentes estilos compositivos.
- En la música renacentista de los siglos XV y XVI, las quintas y octavas perfectas, y las terceras y sextas mayores y menores se consideraban armónicamente consonantes, y todos los demás intervalos disonantes, incluida la cuarta perfecta, que en 1473 fue descrita (por Johannes Tinctoris) como disonante, excepto entre las partes superiores de una sonoridad vertical, por ejemplo, con una tercera de apoyo por debajo ("acordes 6-3").[8] En el período de práctica común, tiene más sentido hablar de acordes consonantes y disonantes, y ciertos intervalos que antes se consideraban disonantes (como las séptimas menores) pasaron a ser aceptables en ciertos contextos. Sin embargo, la práctica del siglo XVI se siguió enseñando a los músicos principiantes durante todo este periodo.
- Hermann von Helmholtz (1821-1894) teorizó que la disonancia era causada por la presencia de beats.[9] von Helmholtz creía además que el batido producido por los parciales superiores de los sonidos armónicos era la causa de la disonancia para intervalos demasiado separados para producir batidos entre la fundamentales.[10] von Helmholtz designó entonces que dos tonos armónicos que compartieran parciales bajos comunes serían más consonantes, ya que producían menos batimentos.[11][12] von Helmholtz no tuvo en cuenta los parciales por encima de la séptima, ya que creía que no eran lo suficientemente audibles como para tener un efecto significativo.[13] A partir de esto von Helmholtz categoriza la octava, quinta perfecta, cuarta perfecta, sexta mayor, tercera mayor y tercera menor como consonantes, en valor decreciente, y otros intervalos como disonantes.
- David Cope (1997) sugiere el concepto de fuerza de intervalo,[14] en el que la fuerza, consonancia o estabilidad de un intervalo viene determinada por su aproximación a una posición inferior y más fuerte, o superior y más débil, en la serie armónica. Véase también: Ley de Lipps-Meyer y #raíz de intervalo
Todos los análisis anteriores se refieren a intervalos verticales (simultáneos).
Simples y compuestos[editar]
Un intervalo simple es un intervalo que abarca como máximo una octava (véase Intervalos principales más arriba). Los intervalos que abarcan más de una octava se denominan intervalos compuestos, ya que pueden obtenerse añadiendo una o más octavas a un intervalo simple (véase abajo para más detalles).[15]
Pasos y saltos[editar]
Los intervalos lineales (melódicos) pueden describirse como pasos o saltos. Un paso, o movimiento conjunto,[16] es un intervalo lineal entre dos notas consecutivas de una escala. Cualquier intervalo mayor se denomina salto (también llamado salto), o movimiento disyuntivo.[16] En la escala diatónica,[7] un paso es una segunda menor (a veces también llamado medio paso) o una segunda mayor (a veces también llamado paso entero), siendo saltos todos los intervalos de una tercera menor o mayores.
Por ejemplo, de Do a Re (segunda mayor) es un paso, mientras que de Do a Mi (tercera mayor) es un salto.
En términos más generales, un paso es un intervalo más pequeño o más estrecho en una línea musical, y un salto es un intervalo más ancho o más grande, donde la categorización de los intervalos en pasos y saltos está determinada por el afinación y el espacio de tono utilizado.
El movimiento melódico en el que el intervalo entre dos tonos consecutivos no es mayor que un paso, o, menos estrictamente, donde los saltos son raros, se denomina movimiento melódico en escalón o conjunto, en oposición a los movimientos melódicos skipwise o disjunto, caracterizados por saltos frecuentes.
Inversión[editar]
Un intervalo puede ser invertido, al subir la nota inferior una octava o bajando la nota superior una octava, aunque es menos usual hablar de las inversiones de unísonos u octavas. Por ejemplo, la cuarta entre un Do grave y un Fa más agudo puede ser invertida para hacer una quinta, con un Fa grave y un Do más agudo. He aquí formas de identificar las inversiones de intervalos:
- Para intervalos diatónicos hay dos reglas para todos los intervalos simples:
- El número de cualquier intervalo y el número de su inversión siempre suman nueve (cuarta + quinta = nueve, en el ejemplo reciente).
- La inversión de un intervalo mayor es uno menor (y viceversa); la inversión de un intervalo justo es otro justo; la inversión de un intervalo aumentado es un disminuido (y viceversa); y la inversión de un intervalo doble aumentado es uno doble disminuido (y viceversa).
- Un ejemplo completo: Mi♭ debajo y Do por encima hacen una sexta mayor. Por las dos reglas anteriores, Do natural debajo y Mi Bemol por encima deben hacer una tercera menor.
- Para intervalos identificados por razón, la inversión es determinada revirtiendo la razón y multiplicando por 2. Por ejemplo, la inversión de una razón 5:4 es una razón 8:5.
- Para intervalos identificados por entero pueden simplemente ser restados de 12. Sin embargo no pueden ser invertidos.
Véase también[editar]
Referencias[editar]
- ↑ Entiéndase como los grados de la escala que se ven afectados por el intervalo.
- ↑ Riemann, Hugo. Teoría General de la Música. Barcelona: Idea Books. p. 67. ISBN 84-8236-324-7.
- ↑ Rousseau, Jean-Jacques ([1768] 2005). Diccionario de Música. Madrid: Akal. pp. Lámina C figura 2. ISBN 978-84-460-2172-8.
- ↑ Error en la cita: Etiqueta
<ref>no válida; no se ha definido el contenido de las referencias llamadasLindleyMarkCampbell - ↑ «MUSICCA». www.musicca.com. Consultado el 14 de febrero de 2024.
- ↑ Véase, por ejemplo, William Lovelock, The Rudiments of Music (Nueva York: St Martin's Press; Londres: G. Bell, 1957): [página requerida], reimpreso 1966, 1970 y 1976 por G. Bell, 1971 por St Martins Press, 1981, 1984 y 1986 Londres: Bell & Hyman. ISBN 9780713507447 (pbk). ISBN 9781873497203
- ↑ a b Error en la cita: Etiqueta
<ref>no válida; no se ha definido el contenido de las referencias llamadasdiatonic - ↑ Drabkin, William (2001). "Cuarta". The New Grove Dictionary of Music and Musicians, segunda edición, editado por Stanley Sadie y John Tyrrell. Londres: Macmillan.
- ↑ Helmholtz, H. L. F. (1877) Sobre las sensaciones del tono como base teórica para la teoría de la música]. Tercera edición inglesa. Ellis, Alexander J. (trad.) (1895). Longmans, Green, And Co. (p. 172) "La rugosidad de hacer sonar dos tonos juntos depende... del número de batimentos producidos en un segundo".
- ↑ Helmholtz, H. L. F. (1877) On the Sensations of Tone as a Theoretical Basis for the Theory of Music. Tercera edición inglesa. Ellis, Alexander J. (trad.) (1895). Longmans, Green, And Co. (p. 178) "La causa de este fenómeno debe buscarse en los batimentos producidos por los parciales altos superiores de tales tonos compuestos".
- ↑ Helmholtz, H. L. F. (1877) On the Sensations of Tone as a Theoretical Basis for the Theory of Music. Tercera edición inglesa. Ellis, Alexander J. (trad.) (1895). Longmans, Green, And Co. (p. 182).
- ↑ Helmholtz, Hermann L. F. On the Sensations of Tone as a Theoretical Basis for the Theory of Music, segunda edición inglesa, traducida por Ellis, Alexander J. (1885) reimpreso por Dover Publications con nueva introducción (1954) ISBN 0-486-60753-4, p. 182d "Así como las coincidencias de los dos primeros tonos parciales superiores nos condujeron a las consonancias naturales de la Octava y la Quinta, las coincidencias de los parciales superiores superiores nos conducirían a otra serie de consonancias naturales. "
- ↑ Helmholtz, H. L. F. (1877) Sobre las sensaciones del tono como base teórica para la teoría de la música. Tercera edición inglesa. Ellis, Alexander J. (trad.) (1895). Longmans, Green, And Co. (p. 183) "Aquí me he detenido, porque el 7º tono parcial está completamente eliminado, o al menos muy debilitado,".
- ↑ Cope, David (1997). Técnicas del compositor contemporáneo, pp. 40-41. New York, New York: Schirmer Books. ISBN 0-02-864737-8.
- ↑ Wyatt, Keith (1998). Armonía y Teoría.... Hal Leonard Corporation. p. 77. ISBN 0-7935-7991-0.
- ↑ a b Bonds, Mark Evan (2006). A History of Music in Western Culture, p.123. 2ª ed. ISBN 0-13-193104-0.
Bibliografía[editar]
- Riemann, H. Teoría general de la música, Barcelona, Idea Books, 2005. ISBN 84-8236-324-7.
- Zamacois, J. Teoría de la música (I/II), Barcelona, Labor, 2007. ISBN 978-84-335-7840-2.
Enlaces externos[editar]
- Visualizar los intervalos en la guitarra Guía completa
- La altura de los sonidos:
 emisión del 13 de oct. del 2019 de El rincón de la teoría, programa de Radio Clásica.
emisión del 13 de oct. del 2019 de El rincón de la teoría, programa de Radio Clásica.
- La distancia entre los sonidos:
 emisión del 20 de oct. del 2019 de El rincón de la teoría.
emisión del 20 de oct. del 2019 de El rincón de la teoría.
- Intervalos armónicos:
 emisión del 10 de nov. del 2019 de El rincón de la teoría.
emisión del 10 de nov. del 2019 de El rincón de la teoría.
- Véase "Intervalo armónico".
 Wikimedia Commons alberga una categoría multimedia sobre intervalos armónicos.
Wikimedia Commons alberga una categoría multimedia sobre intervalos armónicos.
