Grado (matemática)
- Este artículo trata del "grado" tal y como es empleado en el área de las matemáticas. Para otros significados de esta palabra, véase grado.
En matemáticas existen diferentes significados de la palabra grado dependiendo del área matemática de que se trate. Todas las definiciones tienen como resultado un número natural que expresa el grado.
Álgebra[editar]
Grado de un Polinomio[editar]
El grado de un polinomio de una variable es el máximo exponente que posee el monomio sobre la variable; Por ejemplo en 2x3 + 4x2 + x + 7, el término de mayor grado es 2x3; este término tiene una potencia tres en la variable x, y por lo tanto se define como grado 3 o de tercer grado.
Para polinomios de dos o más variables, el grado de un término es la suma de los exponentes de las variables en el término; el grado del polinomio será el monomio de mayor grado. Por ejemplo, el polinomio x2y2 + 3x3 + 4y tiene un grado 4, el mismo grado que el término x2y2.
Grado de congruencia[editar]
Si es un polinomio con coeficientes enteros, el grado de congruencia de es el mayor entero positivo j tal que aj no es congruente con cero respecto del módulo m.
Teoría de Ecuaciones[editar]
En teoría de ecuaciones algebraicas, el grado de una ecuación corresponde a la máxima potencia a la que está elevada la incógnita algebraica de la ecuación. Por ejemplo: la ecuación es de tercer grado en x, siendo de primer grado en la incógnita y. Véase: Ecuación de segundo grado, Ecuación de tercer grado, Ecuación de cuarto grado, Ecuación de quinto grado, etc.
Grado de una extensión[editar]
En álgebra se tiene la extensión de cuerpo y en ella se define el grado como todo espacio vectorial con base, pudiéndose calcular la dimensión de como espacio vectorial sobre , denotado por . a la dimensión de como -espacio vectorial: .
Geometría[editar]
Ángulos[editar]

El "Grado" es la unidad empleada para clasificar los ángulos en las figuras geométricas (generalmente entre dos rectas o segmentos). Existen no obstante varias escalas:
- Grado sexagesimal, cuando la circunferencia se divide en 360 grados en una figura.
- Grado centesimal, cuando la circunferencia se divide en 400 grados.
Teoría de Grados[editar]
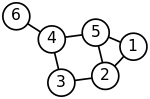
En la teoría de grafos, el grado de un vértice en un grafo es el número de caminos que inciden en el vértice— en otras palabras, el número de líneas que pasan por un nudo del grafo. su utilidad define si una trayectoria por el grafo es o no un camino euleriano. es un sistema de medición Kalet
Estadística[editar]
Grados de Libertad[editar]
En estadística grados de libertad es un estimador del número de categorías independientes en un test particular o experimento estadístico. Se encuentran mediante la fòrmula n-1, donde n=número de sujetos en la muestra (también pueden ser representados por k-1 donde k=número de grupos, cuando se realizan operaciones con grupos y no con sujetos individuales).








![{\displaystyle [L:K]=\dim _{K}(L)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/86be8e9aa101614cad654596e3448c77fa56e3ff)