Diferencia entre revisiones de «Poliedro de Goldberg»

Contenido eliminado Contenido añadido

En renglón

Revisión del 15:53 26 oct 2022

Icosahedral Goldberg polyhedra with pentagons in red
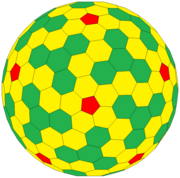$GP(1,4)= {5+,3} Plantilla:Sub$	$GP(4,4)= {5+,3} Plantilla:Sub$
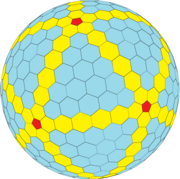$GP(7,0)= {5+,3} Plantilla:Sub$	$GP(3,5)= {5+,3} Plantilla:Sub$
$GP(10,0)= {5+,3} Plantilla:Sub$ Equilateral and spherical

En matemáticas, y más específicamente en combinatoria poliédrica, un poliedro de Goldberg es un politopo convexo hecho de hexágonos y pentágonos. Fueron descritos por primera vez en 1937 por Michael Goldberg (1902-1990). Están definidos por tres propiedades: cada face es un pentágono o un hexágono, exactamente tres caras se encuentran en cada vertex y tienen simetría icosaédrica. No son necesariamente mirror-symmetric; p.ej. $GP(5,3)$ y $GP(3,5)$ son quiralidad (matemáticas) uno del otro. Un poliedro de Goldberg es un poliedro conjugado de un geodesic sphere.

Una consecuencia de Característica de Euler es que un poliedro de Goldberg siempre tiene exactamente doce caras pentagonales. La simetría icosaédrica asegura que los pentágonos sean siempre regular y que siempre haya 12 de ellos. Si los vértices no están restringidos a una esfera, el poliedro se puede construir con caras planas equiláteras (pero no en general equiangulares).

Los ejemplos simples de poliedros de Goldberg incluyen dodecaedro y icosaedro truncado. Se pueden describir otras formas haciendo un movimiento ajedrez knight de un pentágono al siguiente: primero dé pasos $m$ en una dirección, luego gire 60° a la izquierda y dé pasos $n$ . Tal poliedro se denota $GP(m, n).$ Un dodecaedro es $GP(1,0)$ y un icosaedro truncado es $GP(1,1).$

Se puede aplicar una técnica similar para construir poliedros con simetría tetraédrica y simetría octaédrica. Estos poliedros tendrán triángulos o cuadrados en lugar de pentágonos. Estas variaciones tienen subíndices de números romanos que indican el número de lados en las caras que no son hexagonales: $GP Plantilla:Sub (n, m),$ $GP Plantilla:Sub (n, m),$ y $GP Plantilla:Sub (n, m).$

Elementos

El número de vértices, aristas y caras de GP(m,n) se puede calcular a partir de m y n, con T = m² + mn + n² = (m + n' ')² − mn, dependiendo de uno de los tres sistemas de simetría:^[1] El número de caras no hexagonales se puede determinar utilizando la característica de Euler, como se demuestra en here.

Symmetry	Icosahedral	Octahedral	Tetrahedral
Base	Dodecahedron GP_V(1,0)= {5+,3}_1,0	Cubo GP_IV(1,0)= {4+,3}_1,0	Tetraedro GP_III(1,0)= {3+,3}_1,0
Image
Symbol	GP_V(m,n)= {5+,3}_m,n	GP_IV(m,n)= {4+,3}_m,n	GP_III(m,n)= {3+,3}_m,n
Vertices	$20T$	$8T$	$4T$
Edges	$30T$	$12T$	$6T$
Faces	$10T+2$	$4T+2$	$2T+2$
Faces by type	12 {5} and 10(T − 1) {6}	6 {4} and 4(T − 1) {6}	4 {3} and 2(T − 1) {6}

Construcción

La mayoría de los poliedros de Goldberg se pueden construir utilizando Notación de poliedros de Conway a partir de semillas de (T)etraedro, (C)ube y (D)odecaedro. El operador chamfer, c, reemplaza todos los bordes por hexágonos, transformando GP(m,n) a GP(2m,2 n), con un multiplicador T de 4. El operador kis truncado, y = tk, genera GP(3,0), transformando GP(m, n) a GP(3m,3n), con un multiplicador T de 9.

Para formularios de clase 2, el operador dual kis, z = dk, transforma GP(a,0) en GP' '(a,a), con un multiplicador T de 3. Para formularios de clase 3, el operador giratorio, w, genera GP' '(2,1), con un multiplicador T de 7. Un generador de torbellino en sentido horario y antihorario, ww = wrw genera GP(7,0 ) en la clase 1. En general, un torbellino puede transformar un GP(a,b) en GP(a + 3b,2 ab) para a > b y la misma dirección quiral. Si se invierten las direcciones quirales, GP(a,b) se convierte en GP(2a + 3b,a −&nbsp ;2b) si a ≥ 2b, y GP(3a + b,2b − a) si a < 2b.

Examples

Class I polyhedra
Frequency	(1,0)	(2,0)	(3,0)	(4,0)	(5,0)	(6,0)	(7,0)	(8,0)	(m,0)
T	1	4	9	16	25	36	49	64	m²
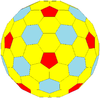
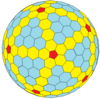
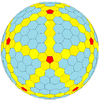
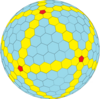
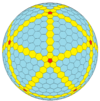
Icosahedral (Goldberg)	regular dodecahedron	chamfered dodecahedron							more
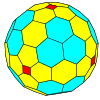
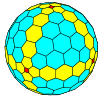
Octahedral	cubo	chamfered cube							more
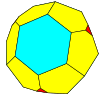
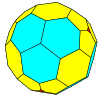
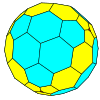
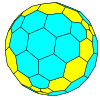
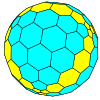
Tetrahedral	tetraedro	chaflán (geometría)							more

Class II polyhedra
Frequency	(1,1)	(2,2)	(3,3)	(4,4)	(5,5)	(6,6)	(7,7)	(8,8)	(m,m)
T	3	12	27	48	75	108	147	192	3m²
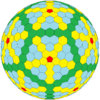
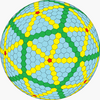
Icosahedral (Goldberg)	icosaedro truncado								more
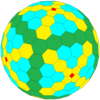
Octahedral	octaedro truncado								more
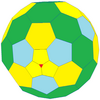
Tetrahedral	tetraedro truncado								more

Class III polyhedra
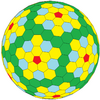
Frequency	(1,2)	(1,3)	(2,3)	(1,4)	(2,4)	(3,4)	(5,1)	(m,n)
T	7	13	19	21	28	37	31	m²+mn+n²
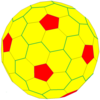
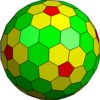
Icosahedral (Goldberg)								more
Octahedral		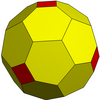						more
Tetrahedral		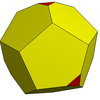						more

Véase también

Notas

↑ Clinton’s Equal Central Angle Conjecture, JOSEPH D. CLINTON

Referencias

Goldberg, Michael (1937). «A class of multi-symmetric polyhedra». Tohoku Mathematical Journal 43: 104-108.
Joseph D. Clinton, Conjetura del ángulo central igual de Clinton
Hart, George (2012). «Goldberg Polyhedra». En Senechal, Marjorie, ed. Shaping Space (2nd edición). Springer. pp. 125-138. ISBN 978-0-387-92713-8. doi:10.1007/978-0-387-92714-5_9. [1]
Hart, George (June 18, 2013). «Mathematical Impressions: Goldberg Polyhedra». Simons Science News.
Schein, S.; Gayed, J. M. (25 de febrero de 2014). «Fourth class of convex equilateral polyhedron with polyhedral symmetry related to fullerenes and viruses». Proceedings of the National Academy of Sciences (en inglés) 111 (8): 2920-2925. Bibcode:2014PNAS..111.2920S. ISSN 0027-8424. PMC 3939887. PMID 24516137. doi:10.1073/pnas.1310939111.

Enlaces externos

Icosaedra geodésica dual
Variaciones de Goldberg: Nuevas formas para jaulas moleculares Los hexágonos planos y los pentágonos se unen en un nuevo giro sobre el viejo poliedro, por Dana Mackenzie , 14 de febrero de 2014

Datos: Q15735747
Multimedia: Goldberg polyhedra / Q15735747

[1] Clinton’s Equal Central Angle Conjecture, JOSEPH D. CLINTON

[1]