Viscoelasticidad
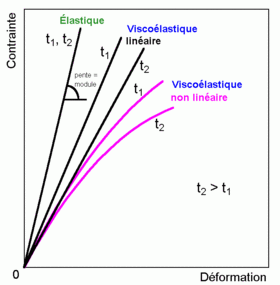
La viscoelasticidad es un tipo de comportamiento reológico anelástico que presentan ciertos materiales que exhiben tanto propiedades viscosas como propiedades elásticas cuando se deforman.
En un sólido viscoelástico:
- La deformación generalmente depende del tiempo; aun en ausencia de fuerzas, la velocidad de deformación puede ser diferente de cero.
- Las tensiones y esfuerzos resistidos dependen tanto de la deformación como de la velocidad de deformación; por tanto la ecuación constitutiva que relaciona tensiones y deformaciones debe tener la forma:
- Existe relajación de tensiones; es decir, si se somete el sólido a una deformación uniforme con el paso del tiempo las tensiones disminuyen manteniéndose constante la deformación.
- Existe deformación por fluencia lenta; es decir, sometido a una tensión constante y uniforme la deformación aumenta ligeramente con el tiempo.
Existen materiales que presentan dependencia de la velocidad de deformación, por lo que puede darse la característica (2) anterior y no ser viscoelásticos. Las características (3) y (4) a veces se toman como características necesarias para clasificar a un material dentro de los materiales viscoelásticos.
Físicamente las propiedades elásticas son el resultado de desplazar ligeramente los átomos de su posición de equilibrio a lo largo de planos cristalográficos, mientras las propiedades viscosas proceden de la difusión de átomos o moléculas en el interior del material.[1]
Viscoelasticidad lineal[editar]
Un material viscoelástico lineal general es un material para el cual existe una relación lineal entre la tensión y sus derivadas y la deformación y sus derivadas, en el caso unidimensional la relación más general posible de un material viscoelástico lineal es:[2]
(1a)
En este caso usando transformadas de Laplace y si y , la expresión () puede escribrise simplemente como:
(1b)
Siendo . Cuando , la expresión equivalente a () es más simple:
(1c)
Aunque esta expresión no se usa porque en la práctica no se conocen materiales que se ajusten bien a este tipo de ley. Así que aquí se restringirá la discusión a .
Los dos modelos viscoelásticos más conocidos, el de Maxwell y el de Kelvin-Voigt son casos particulares de () que satisfacen . En ambos , y para el de Kelvin-Voigt y para el de Maxwell.
Creep y relajación[editar]
Bajo los mismos supuestos anteriores, puede probarse que un material viscoelástico lineal admite una caracterización matemática en que la respuesta de creep y de relajación de carga admiten una separación en forma de suma. Los modelos de viscoelasticidad lineal pueden ser representados mediante una ecuación integral de Volterra que relaciona la tensión y la deformación, es decir, mediante una expresión del tipo:
(2a)
o también:
(2b)
donde:
- , es el tiempo.
- , es la tensión mecánica.
- , es la deformación o elongación.
- y , son los módulos elásticos longitudinales para el creep y la relajación.
- , es la función de creep.
- , es la función de relajación.
La viscoelasticidad lineal tiene un rango de aplicación válido sólo para deformaciones muy pequeñas. Para el caso de un material perfectamente elástico tanto la función de creep como la de relajación son idénticamente nulas.
Ecuaciones constitutivas de viscoelasticidad lineal[editar]
Existen diversos modelos constitutivos para materiales viscoelásticos lineales. Esos modelos incluyen el modelo de Maxwell, el modelo de Kelvin-Voigt y el modelo de sólido viscoelástico lineal estándar que combina los dos modelos anteriores. Todos estos modelos descomponen la tensión y deformación en dos sumandos, uno que representa los efectos elásticos y otro que representa los efectos viscosos, siendo estos modelos, interpretables en términos de muelles y amortiguadores. Cada uno de estos modelos difiere en la disposición de los muelles y amortiguadores.
Otra propiedad interesante es que las ecuaciones constitutivas también pueden ser interpretadas en términos de circuitos eléctricos, en los que la tensión mecánica sería el equivalente del voltaje y la velocidad de deformación sería equivalente a la intensidad de corriente. El módulo elástico sería equivalente a la capacitancia del circuito (que mide la capacidad de almacenaje de energía) y la viscosidad a la resistencia del circuito (que mide la capacidad de disipar energía).
Modelo de Maxwell[editar]

El modelo de Maxwell es un caso particular de la expresión () en el que , también llamado material viscoelástico de "larga memoria". Una virtud del modelo de Maxwell es que admite una representación intuitiva en términos de muelles y disipadores (amortiguadores), más concretamente el modelo de Maxwell representa un elemento elástico dispuesto en serie con un amortiguador. La ecuación constitutiva del modelo viene dada por la siguiente ecuación diferencial de primer orden:
(3a).
Este modelo predice que en un material puesto bajo deformación constante, las tensiones gradualmente se relajarán hasta hacerse cero. Igualmente predice que si el material se pone a tensión constante la deformación tendrá dos componentes, un primer componente elástico que aparece instantáneamente y una deformación a largo plazo de tipo viscoso que crecerá con el tiempo mientras sigan existiendo fuerzas. Alternativamente la ecuación constitutiva de este modelo puede escribirse como:
.
Integrando por partes el último término se puede obtener reescribir la expresión anterior en términos de la función de relajación y la velocidad de deformación:
(3b).
Para obtener la de función de creep se integra directamente (), e integrando por partes se obtiene:
(3c).
Y no es posible encontrar una función ordinaria para expresar lo anterior en la forma ().
El modelo de Maxwell predice que la tensión decaerá exponencialmente con el tiempo en un polímero sometido a deformación constante, lo cual se ajusta bastante bien a lo observado experimentalmente para muchos polímeros. Sin embargo, una limitación importante es que no predice el comportamiento de "creep" de muchos polímeros de manera demasiado fidedigna ya que en este caso predice un aumento lineal de la deformación con el tiempo si la tensión es constante, sin embargo la mayor parte de los polímeros muestran una tasa de deformación decreciente con el tiempo. Las principales aplicaciones de este modelo son la modelización de los polímeros termoplásticos cerca de su temperatura de fusión, la del hormigón fresco y la de numerosos metales cerca de su punto de fusión.
Modelo de Voigt-Kelvin[editar]
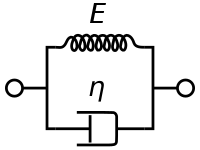
El modelo de Kelvin-Voigt o modelo de Voigt es un caso particular de la expresión () en el que , también llamado material viscoelástico de "corta memoria". Al igual que el modelo anterior admite una representación simple en términos de muelles y amortiguadores: el modelo es representable por un amortiguador newtoniano y un muelle que sigue la ley de Hooke conectado en paralelo al amortiguador, tal como muestra la figura. La ecuación constitutiva del modelo puede expresarse como ecuación diferencial de primer orden:
(4a)
Este modelo representa un sólido que sufre deformación viscoplástica reversible. Bajo la aplicación de una tensión constante el material se deforma a un ritmo progresivamente más lento, llegando asintóticamente a un estado cuasiestacionario. Cuando se eliminan las fuerzas exteriores que generan las tensiones, el material se relaja hasta su estado no deformado original. En una situación de tensión constante (creep), el modelo es bastante realista y predice deformaciones que tienden al límite σ/E para tiempos grandes.
En este caso la función de relajación viene dada por la delta de Dirac (de ahí el nombre de "corta memoria") ya que:
(4b)
Para obtener la función de creep se busca la transformada de Laplace de () de donde es fácil aislar la transformada de la deformación y aplicando la transformada inversa se llega fácilmente a que:
Integrando por partes esta última expresión se llega a una expresión que contiene la función de creep o fluencia lenta:
(4c)
Este modelo se usa para explicar el comportamiento de "creep" de los polímeros. Aunque, al igual que el modelo de Maxwell, el modelo de Kelvin-Voigt tiene limitaciones empíricas. Aunque modela muy bien el "creep" con respecto a la relajación el modelo generalmente se ajusta menos al comportamiento de los materiales viscoelásticos. Las aplicaciones principales del modelo son la modelización de polímeros orgánicos, goma, caucho y madera cuando la carga no es muy elevada.
Modelo estándar de sólido viscoelástico[editar]
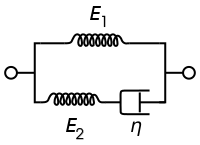
Los dos últimos modelos expuestos tienen limitaciones en cierto modo complementarias. Por esa razón se considera que un modelo que combine características de ambos puede ser un modelo razonable de sólido viscoelástico. La ecuación constitutiva de este modelo viene dada por la siguiente ecueción diferencial:
(5a)
Usando transformadas de Laplace, despejando la transformada de la tensión y antitransformando se obtiene una ecuación de tipo Volterra como en los casos anteriores, que tiene la forma:
Una integración por partes del último término permite escribir en términos de la función de relajación y la velocidad de deformación:
(5b)
Modelo de Burgers[editar]
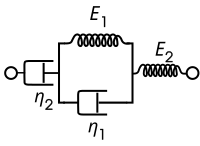
El modelo de Burgers combina características de los modelos de Maxwell y Kevin-Voigt. La ecuación constitutiva se puede escribir como de manera compacta como ecuación diferencial de segundo orden:
(6a)
Donde , usando la transformada de Laplace se puede integrar de manera mecánica la ecuación anterior (suponiendo que inicialmente tanto la tensión, como la deformación y sus tasas de cambio son nulas):
De donde se obtiene, integrando por partes, la función de relajación:
(6b)
Y también mediante la transformada de Laplace se obtiene la expresión:
Donde:
Que, integrada por partes, permite obtener la función de creep:
(6c)
Modelo de Wiechert[editar]

El modelo de Wiechert o Maxwell-Wiechert (a veces también modelo generalizado de Maxwell) es una generalización del modelo viscolástico estándar (y por tanto también del modelo de Maxwell simple). Este modelo toma en cuenta que la relación no ocurre según un único ritmo característico, sino según una distribución de escalas de tiempo. Esto sucede porque existen segmentos moleculares de diferentes longitudes, contribuyendo los más cortos menos que los más largos, de ahí la diversidad de escalas de tiempo. El modelo de Weichert modeliza esto mediante tantos conjuntos de muelle-amortiguador como sean necesarios para aproximar la distribución de escalas de tiempo. La figura de la derecha representa un posible modelo de Wiechert.[3][4][5] Dado un modelo de Maxwell-Wiecher con elementos cuyos módulos de elasticidad longitudinales sean con , y cuyas viscosidades sean con , y con tiempos de relajación dados por , entonces, la forma general del modelo de Maxwell-Wiechert viene dad por:
(7a)
Partiendo igual que en los casos anteriores de un estado natural no deformado y usando el formalismo de la transformada de Laplace tenemos que la tensión se expresa como:
Por lo haciendo integración por partes se llega a que:
(7b)
Donde la función de relación tiene directamente la forma de una serie de Prony.
Este modelo encuentra aplicación en metales y aleaciones metálicas a temperaturas más bajas que un cuarto de su temperatura absoluta de fusión (expresada en K).
Viscoelasticidad no lineal[editar]
Modelos unidimensionales[editar]
La viscosidad no lineal ocurre cuando las funciones de creep y de relajación de carga no se pueden separar. Esto ocurre en deformaciones grandes, si el material cambia sus propiedades durante la deformación, si los tiempos de la deformación son lo suficientemente largos o si interviene algún otro tipo de relajación.
Existe una pléyade de modelos no lineales, dependientes de unas pocas constantes características del material cuyos valores pueden ajustarse al resultado de los experimentos.[6] Entre ellos pueden citarse:
- Modelo de Eyring:
- Modelo de Ostwald-de Waele:
- Modelo de Briant:
- Modelo de Powell-Eyring:
- Modelo de Robertson-Stiff:
- Modelo de Shangraw-Grim-Mattocks:
- Modelo de Sisko:
- Modelo de Williamson:
- Modelo de Carreau:
En estos modelos las constantes toman valores positivos y deben determinarse por comparación con experimentos, ya que no parecen tener un significado teórico profundo. De hecho estos modelos son esencialmente empíricos y no existen razones teóricas que los sustente aparte de que se ajustan experimentalmente a diversos materiales. Sólo unos pocos de estos modelos admiten generalizaciones tridimensionales consistentes.
Teoría general[editar]
La teoría general de materiales viscoelásticos para deformación finita para materiales simples, se basa en asumir una serie de axiomas razonables que limitan la forma funcional de las ecuaciones más generales posibles, entre estas condiciones se emplean usualmente:[7]
- Principio de localidad y determinismo
- Principio de objetividad material (o covarianza)
- Dependencia en derivadas primeras del gradiente de deformación.
Se pueden dar diferentes ecuaciones diferenciales para el tensor tensión de Cauchy:
donde:
- son respectivamente las coordenadas materiales, espaciales y el tiempo.
- es el tensor [izquierdo] de Cauchy para las deformaciones.
- son el gradiente de deformación y su inverso.
- representa la parte de la respuesta elástica.
- representa la parte de la respuesta propiamente viscoelástica.
Para el primer tensor de Piola-Kirchhoff se tiene:
donde:
- da la respuesta elástica.
- da la respuesta propiamente viscoelástica.
Véase también[editar]
Referencias[editar]
- ↑ Meyers and Chawla (1999), Mechanical Behavior of Materials, 98-103.
- ↑ A. M. Freudenthal et Geiringer, 1958
- ↑ Roylance, David (2001); "Engineering Viscoelasticity", 14-15
- ↑ Wiechert, E (1889); "Ueber elastische Nachwirkung", Dissertation, Königsberg University, Germany
- ↑ Wiechert, E. (1893); "Gesetze der elastischen Nachwirkung für constante Temperatur", Annalen der Physik, Vol. 286, issue 10, p. 335–348 and issue 11, p. 546–570
- ↑ Aleksey D. Drozdov: Finite elasticity and viscoelasticity: a course in the nonlinear mechanics of Solids
- ↑ Drapaca, C. S., S. Sivaloganathan, and G. Tenti. "Nonlinear constitutive laws in viscoelasticity." Mathematics and mechanics of solids 12.5 (2007): 475-501.
Bibliografía[editar]
- Freudenthal, A. M. y Geiringer, H: "The mathematical theories of inelastic continuum", Handbuch der Physik - Encyclopedia of Physics, VII, Elasticity and Plasticity. Berlin-Göttingen-Heidelberg: Springer 1958.
- Macosko, C. W.Rheology principles, measurements, and applications, VCH Publ. Inc, 1994, New York.
- Holzapfel, A. G. Nonlinear solid mechanics, 2000.


























![{\displaystyle \sigma (t)=E\varepsilon (t)+\int _{0}^{t}\left[Ee^{-{\frac {E}{\eta }}(t-\tau )}{\dot {\varepsilon }}(\tau )\right]d\tau ,\qquad F(\tau )=Ee^{-{\frac {E}{\eta }}\tau }}](https://wikimedia.org/api/rest_v1/media/math/render/svg/fd60311e713f358a1a43077c8d8e6cf3122b5966)

![{\displaystyle \varepsilon (t)={\frac {\sigma }{E}}+\int _{0}^{t}{\frac {1}{\eta }}\sigma (\tau )d\tau ={\frac {\sigma }{E}}+\int _{0}^{t}\left[{\frac {t-\tau }{\eta }}\right]{\dot {\sigma }}(\tau )d\tau ,\qquad K(\tau )={\frac {\tau }{\eta }}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/2d069bfc4a0b46b36060ace465ae0741f4a22295)









![{\displaystyle \sigma (t)=(E_{1}+E_{2})\varepsilon (t)+\int _{0}^{t}\left[E_{2}e^{-{\frac {E_{2}}{\eta }}(t-\tau )}{\dot {\varepsilon }}(\tau )\right]d\tau ,\qquad F(\tau )=E_{2}e^{-{\frac {E_{2}}{\eta }}\tau }}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b8d3432d996625998d359f2ba9652fc971549bff)



























![{\displaystyle {\boldsymbol {\sigma }}=\mathbf {F} (X,t)\left[\mathbf {f} _{1}(\mathbf {C} (X,t))+\Phi _{1}({\bar {\mathbf {E} }}(X,\cdot ),\mathbf {C} (X,t))\right]\mathbf {F} ^{T}(X,t)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/3c68a1f316dee28e51c8d667da9fd87fe7ea2051)



![{\displaystyle {\bar {\mathbf {E} }}(X(x),s)=\mathbf {F} ^{T}(X,t)[{\hat {\mathbf {E} }}_{t}(x(X),t-s)]\mathbf {F} (X,t)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/cfff4dabe2921366f36d8503239b62519265d094)

![{\displaystyle {\hat {\mathbf {C} }}_{t}(x,s)=\mathbf {F} ^{-T}(x,t)[\mathbf {C} (X(x),s)]\mathbf {F} ^{-1}(x,t)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/7cd497108f169140cdb00d26a49808866a5210d4)




