Transformada de Radon



En matemáticas, la transformada de Radon bidimensional, llamada así por Johann Radon, es una transformación integral que consiste en la integral de una función sobre el conjunto de rectas.
Por ejemplo, si una línea la representamos por , donde es la mínima distancia desde la recta al origen y es el ángulo que forma el eje con el vector posición del punto de la recta más cercano al origen, entonces
En un espacio -dimensional la transformada de Radon es la integral de una función sobre hiperplanos. La integral de una función sobre un conjunto de rectas en un espacio -dimensional se le denomina transformada de rayos-X, aunque a veces este término es adoptado por la transformada de Radon.
En el contexto de las tomografías la transformada de Radon se le suele llamar senograma puesto que la transformada de Radon de una función delta tiene como respuesta característica un seno. En consecuencia, la representación gráfica de la transformada de Radon de un conjunto de pequeños objetos parece una colección de senos con diferentes fases y amplitudes.
Esta transformada en su versión bidimensional y tridimensional fue introducida en un artículo en 1917 por Johann Radon, quien, a su vez, generó una formulación para la transformación inversa. Posteriormente, la antitransformada fue generalizada en el contexto de la geometría integral.
La transformada de Radon es útil en los TAC's (tomografía axial computarizada) y en la solución de ecuaciones en derivadas parciales hiperbólicas.
Teorema de las secciones de Fourier[editar]
La transformada de Radon está estrechamente relacionada con la transformada de Fourier. Para una función de una variable, se define la transformada de Fourier de la siguiente forma
y para una función de bidimensional de variable
por conveniencia cambiamos la nomenclatura de la siguiente forma
puesto que tomaremos la transformada de Fourier respecto la variable . El teorema de las secciones de Fourier se enuncia de la siguiente forma:
donde
Este resultado da una fórmula explícita para la inversión de la transformada de Radon, y además nos da las condiciones para conocer en qué espacios de funciones la transformada de Radon es invertible. Sin embargo, esta igualdad no es útil desde un punto de vista numérico.
Retroproyección filtrada[editar]
 |
 |
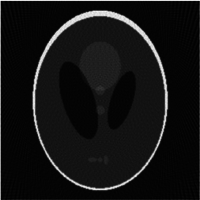 |
| Fantasma de Shepp-Logan; Transformada de Radon; y Transformada de Radon inversa | ||
Existe un algoritmo inverso de la transformada de Radon computacionalmente eficiente para el caso bidimensional llamado retroproyección filtrada. Primeramente consideremos el operador adjunto de :
Este operador recibe el nombre de 'retroproyector' puesto que coge las proyecciones sobre las rectas y las 'esparce' o retroproyecta para producir una imagen. Se puede observar como este operador no es la transformada inversa de Radon.
Definimos el siguiente filtro rampa de una variable
si ahora aplicamos el teorema de las secciones de Fourier y cambiamos las variables de integración, observamos que para una función de dos variables, y
lo que significa que la imagen original puede ser recuperada del 'sinograma' aplicando un filtro rampa (sobre la variable ) y entonces retroproyectando. Como que el paso de filtrado puede ser implementado de forma eficiente (mediante técnicas de procesamiento digital de señales) y la retroproyección no es más que una acumulación de valores en los píxeles de la imagen, resulta un algoritmo altamente eficiente, por lo que se trata de un algoritmo ampliamente usado.
Véase también[editar]
Referencias y enlaces externos[editar]
- Deans, Stanley R. (1983). The Radon Transform and Some of Its Applications. Nueva York: John Wiley & Sons.
- Frank Natterer, The Mathematics of Computerized Tomography (Classics in Applied Mathematics, 32), Society for Industrial and Applied Mathematics. ISBN 0-89871-493-1
- Frank Natterer and Frank Wubbeling, Mathematical Methods in Image Reconstruction, Society for Industrial and Applied Mathematics. ISBN 0-89871-472-9
- Weisstein, Eric W. «RadonTransform». En Weisstein, Eric W, ed. MathWorld (en inglés). Wolfram Research.





=\int _{-\infty }^{\infty }\int _{-\infty }^{\infty }f(x,y)\delta (x\cos \theta +y\sin \theta -s)\,dx\,dy.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/80d9949702246e95a75375dabff1b6cd4e35f11a)




=R[f](s,\theta )}](https://wikimedia.org/api/rest_v1/media/math/render/svg/1431bbfd85c0f82fb5c91fa6906f7cc504ed90e7)
![{\displaystyle {\widehat {R_{\theta }[f]}}(\sigma )={\sqrt {2\pi }}{\hat {f}}(\sigma \mathbf {n} (\theta ))}](https://wikimedia.org/api/rest_v1/media/math/render/svg/bb05a7055ce896c3ba4aa5ed769c94d69b1c4918)


=\int _{\theta =0}^{2\pi }g(\theta ,\mathbf {n} (\theta )\cdot \mathbf {x} )\,d\theta ,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/2c8b11ab0b5cbb4867f97e4754f91a90d2645679)

![{\displaystyle {\widehat {H[h]}}(\omega )=|{w}|{\hat {h}}({\omega })}](https://wikimedia.org/api/rest_v1/media/math/render/svg/78bf31794bcd4fa2e68bb11a5d6b513fd434b391)

![{\displaystyle g=R[f]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/1c26a6f199ff04b73e9435b233747d0afead6d2c)
![{\displaystyle f={\frac {1}{4\pi }}R^{*}H[g]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c9af5c8bf3132c7e1b27b26fc566dc983fcf308e)
