Teoría del estado de transición
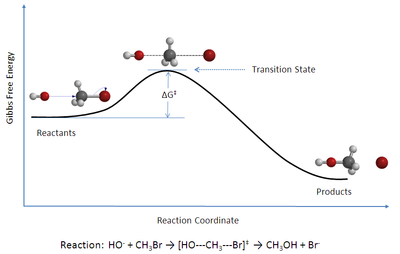
La teoría del estado de transición es una teoría que explica la velocidad de reacción de reacciones químicas elementales. La teoría asume la existencia de un tipo especial de equilibrio químico (casi-equilibrio) entre los reactivos y el complejo activado o estado de transición, una estructura intermedia inestable por su alta energía.[1]
Esta teoría se emplea fundamentalmente para comprender cómo se desarrollan las reacciones químicas pero no ha tenido mucho éxito en su objetivo inicial de calcular las constantes de velocidad para lo cual se requiere un conocimiento preciso de las superficies de energía potencial.[2] Sí ha permitido calcular las entalpías estándar de activación (Δ‡Hº), las entropías estándar de activación (Δ‡Sº), las energías libres de activación (Δ‡Gº) de una determinada reacción si se ha determinado experimentalmente su constante de velocidad. (La notación ‡ se refiere a que el valor en cuestión está medido en el 'estado de transición'.)
Esta teoría se desarrolló simultáneamente en 1935 por Henry Eyring, en la universidad de Princeton, y por Meredith Gwynne Evans y Michael Polanyi de la Universidad de Mánchester.[3][4] También se conoce esta teoría con el nombre de “teoría del complejo activado”, “teoría de velocidades absolutas”, y “teoría de las velocidades absolutas de reacción”.[5]
Antes del desarrollo de esta teoría, la ley de velocidad de Arrhenius era usada ampliamente para determinar barreras de energía de una reacción (diferencia de energía del complejo activado menos la de los reactivos). La ecuación de Arrhenius surge de observaciones empíricas e ignora toda consideración sobre el mecanismo, como por ejemplo si están implicados uno o más estados intermedios en la conversión global de un reactivo en un producto.[6] Por lo tanto, fue necesario un desarrollo posterior para comprender los dos parámetros asociados con esta ley, el factor preexponencial (A) y la energía de activación (Ea). La teoría que condujo a la ecuación de Eyring trata con éxito estas dos cuestiones, transcurriendo 46 años entre la publicación de la ley de velocidad de Arrhenius en 1889 y la ecuación de Eyring basada en la teoría del estado de transición en 1935. En este período, el trabajo de muchos científicos e investigadores contribuyó significativamente al desarrollo de esta teoría.
Teoría[editar]
Las ideas básicas de la teoría del estado de transición son las siguientes:
- 1. Las velocidades de las reacciones se conocen estudiando los complejos activados que se encuentran en la cima (punto superior) de una superficie de energía potencial. No son importantes los detalles de formación de estos complejos activados.
- 2. Los complejos activados están en un equilibrio especial (cuasi-equilibrio) con las moléculas de reactivo.
- 3. Los complejos activados pueden convertirse en productos lo cual permite a la teoría cinética calcular la velocidad de esa conversión.
Desarrollo[editar]
En el desarrollo de la teoría del estado de transición,, se han seguido tres enfoques, como se muestra a continuación:
Enfoque termodinámico[editar]
En 1884, Jacobus Henricus van't Hoff propuso la ecuación de Van't Hoff que describe que la constante de equilibrio de una reacción reversible depende de la temperatura:
donde es la variación de energía interna, es la constante de equilibrio de la reacción, es la constante universal de los gases ideales, y es la temperatura termodinámica. Basándose en datos experimentales, en 1889, Svante Arrhenius propuso una expresión similar para la constante de velocidad de una reacción, dada por:
La integración de esta expression conduce a la ecuación de Arrhenius:
La constante es llamada factor de frecuencia o coeficiente preexponencial, y es la energía de activación. Aunque a comienzos del siglo XX la ecuación de Arrhenius era comúnmente aceptada, la interpretación física de A y E resultaba vaga. Esto llevó a muchos investigadores en cinética química a ofrecer diferentes teorías sobre cómo ocurrían las reacciones químicas, en un intento de relacionar A y E con la dinámica molecular directamente responsable de las reacciones químicas.
En 1910, René Marcelin introdujo el concepto de energía libre de Gibbs estándar de activación. Su ecuación se escribe:
A la vez que Marcelin desarrollaba su formulación, los químicos holandeses Philip Abraham Kohnstamm, Frans Eppo Cornelis Scheffer, y Wiedold Frans Brandsma introdujeron por vez primera la entropía estándar de activación y la entalpía estándar de activación. Ellos propusieron la siguiente ecuación para la constante de velocidad de reacción
La naturaleza o significado de la constante seguía sin estar clara.
Enfoque a partir de la teoría cinética[editar]
Entre 1916 y 1918, Max Trautz y William Lewis estudiaron la velocidad de reacción usando la teoría de colisiones, basada en la teoría cinética de gases. La teoría de colisiones considera a las moléculas de los reactivos como esferas rígidas que chocan entre sí; esta teoría no considera los cambios de entropía.
Lewis aplicó su tratamiento a la siguiente reacción y obtuvo una buena concordancia con los resultados experimentales.
- 2HI → H2 + I2
Sin embargo, más tarde aplicó el mismo tratamiento a otras reacciones y encontró discrepancias grandes entre resultados teóricos y experimentales .
Enfoque a partir de la mecánica estadística[editar]
La mecánica estadística jugó un papel significativo en el desarrollo de la teoría del estado de transición. Sin embargo, la aplicación de la Mecánica estadística a la teoría del estado de transición se desarrolló muy lentamente porque, a mediados del siglo XIX, James Clerk Maxwell, Ludwig Boltzmann, y Leopold Pfaundler publicaron varios artículos discutiendo las reacciones en equilibrio y las velocidades de reacción, en términos del movimiento molecular y la distribución estadística de las velocidades moleculares.
No fue hasta 1912 cuando el químico francés A. Berthoud usó la ley de distribución de Maxwell-Boltzmann para obtener una expresión para laconstante de velocidad
donde a y b son constantes relacionadas con términos de energía.
Dos años después, René Marcelin hizo una contribución esencial considerando el progreso de una reacción química como el movimiento de un punto en un espacio de fases. Luego aplicó los procedimientos mecánico-estadísticos de Gibbs y obtuvo una expresión similar a la que había obtenido anteriormente a partir de consideraciones termodinámicas.
En 1915, otra importante contribución fue realizada por el físico británico James Rice. Basados en su análisis estadístico, concluyó que la constante de velocidad es proporcional al "incremento crítico". Sus ideas fueron desarrolladas más tarde por Richard Chace Tolman. En 1919, el físico austriaco Karl Ferdinand Herzfeld applicó la mecánica estadística a la constante de equilibrio y la teoría cinética a la constante de velocidad de la reacción inversa, k-1, para la disociación reversible de una molécula diatómica.
Obtuvo la siguiente ecuación para la constante de velocidad de la reacción directa:
donde:
- es la energía de disociación en el cero absoluto,
- es la constante de Boltzmann,
- es la constante de Planck,
- es la temperatura termodinámica, y
- es la frecuencia vibracional del enlace.
Esta expresión es muy importante ya que es la primera vez que el factor , que es un componente crítico de la teoría del estado de transición, aparecía en una ecuación de velocidad.
En 1920, el químico americano Richard Chase Tolman desarrolló adicionalmente la idea de Rice del "incremento crítico". Concluyó que el "incremento crítico" (ahora llamado energía de activación) de una reacción es igual a la energía media de todas las moléculas sometidas a reacción menos la energía media de todas las moléculas de reactivo.
Superficies de energía potencial[editar]
El concepto de superficie de energía potencial fue muy importante en el desarrollo de la teoría del estado de transición. La base de este concepto fue establecida por René Marcelin. Él teorizó que el progreso de una reacción química podía describirse como un punto en una superficie de energía potencial con coordenadas de momentos atómicos y distancias.
En 1931, Eyring y Polanyi construyeron una superficie de energía potencial para la reacción inferior. Esta superficie es un diagrama tridimensional basado en los principios mecano-cuánticos así como en datos experimentales de frecuencias vibracionales y energías de disociación.
- H + H2 → H2 + H
Un año después de la construcción de Eyring y Polanyi, H. Pelzer y Eugene Wigner hicieron una importante contribución siguiendo el progreso de una reacción sobre una superficie de energía potencial. La importancia de este fue debida a ser la primera vez que se discutía el concepto de punto de silla o punto singular en una superficie de energía potencial. Concluyeron que la velocidad de una reacción se determina por el movimiento del sistema a través de ese punto de silla.
Derivación de la ecuación de Eyring[editar]
La única característica importante añadida por Eyring, Polanyi y Evans fue la noción de que los complejos activados están en cuasi-equilibrio con los reactivos. La velocidad es por tanto directamente proporcional a la concentración de esos complejos multiplicado por la frecuencia (kBT/h) con la que se convierten en productos.
Suposición del cuasi-equilibrio[editar]
Hay que resaltar que el cuasi-equilibrio[7] es diferente del equilibrio químico clásico pero puede describirse usando el tratamiento termodinámico. Considérese la reacción inferior:
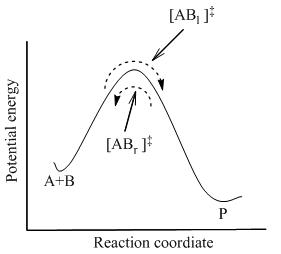
donde se ha alcanzado el equilibrio entre todas las especies del sistema incluyendo los complejos activados, [AB]‡ . Usando la mecánica estadística, la concentración de [AB]‡ puede calcularse en términos de la concentración de A y B.
La teoría del estado de transición postula que aun cuando los reactivos y productos no estén en equilibrio entre sí, los complejos activados están en cuasi-equilibrio con los reactivos. Como se ilustra en la Figura 2, para cualquier instante de tiempo, habrá algo de complejo activado, y algunas de esas partículas eran moléculas de reactivo un instante antes, las cuales serán notadas [ABl]‡ (ya que se están moviendo de izquierda a derecha). El resto de ellas eran moléculas de producto en un instante anterior [ABr]‡. Ya que el sistema está en completo equilibrio, las concentraciones de [ABl] ‡ y [ABr]‡ son iguales, por lo que cada concentración es igual a la mitad de la concentración total de complejos activados:
y
Si las moléculas de producto son frecuentemente retiradas del sistema reaccionante, el flujo de esos complejos activados que comenzaron como productos ([ABr]‡ ) se detendrá; sin embargo, todavía habrá un flujo de izquierda a derecha. Por lo tanto, la suposición es que la velocidad de flujo de izquierda a derecha no se ve afectada por la retirada de los productos; en otras palabras, se supone que los flujos en las dos direcciones son independientes entre sí.
En la teoría del estado de transición, es importante darse cuenta de que cuando se dice que los complejos activados están en equilibrio con los reactivos, se refiere solamente a aquellos complejos activados ([ABl] ‡) que eran moléculas de reactivo en un estado inmediato.
La constante de equilibrio : para el cuasi-equilibrio puede escribirse como:
Por lo tanto, la concentración del estado de transición AB‡ es:
Por lo tanto, la ecuación de velocidad para la producción de producto es:
donde la constante de velocidad k viene dada por:
k‡ es directamente proporcional a la frecuencia del modo vibracional responsable de convertir el complejo activado en producto; la frecuencia de este modo vibracional es ν. Todas las vibraciones no conducen necesariamente a la formación de producto, por eso una constante de proporcionalidad κ, referida al coeficiente de transmisión, se introduce para tener en cuenta este effecto. Así k‡ puede reescribirse como:
Para la constante de equilibrio K‡ , la mecánica estatisdica conduce a una expression dependiente de la temperatura dada por:
donde:
Combinando las nuevas expresiones para k‡ y K‡, se puede escribir una nueva expresión de laconstante de velocidad, que está dada por:
Ya que , la expresión de la constante de velocidad puede expandirse, dando la ecuación de Eyring:
La expresión de la constante de velocidad de la teoría del estado de transición puede usarse para calcular Δ‡G⦵, Δ‡H⦵, Δ‡S⦵, e incluso Δ‡V (el volumen de activación) usando datos experimentales de velocidad.
Limitaciones de la teoría del estado de transición[editar]
En general, la teoría del estado de transición ha suministrado a los investigadores una base conceptual para comprender cómo tienen lugar las reacciones químicas. Aun cuando la teoría es ampliamente aceptada, tiene limitaciones. Por ejemplo, la teoría supone que una vez que la estructura de transición comienza a bajar por la superficie de energía potencial, conduce a un producto (o un conjunto de productos). Sin embargo, en algunas reacciones, el estado de transición puede atravesar la superficie de energía potencial de tal manera, que conduce a una inesperada selectividad de producto no predicha por la teoría del estado de transición (un ejemplo de tales reacciones es la descomposición térmica de diazobiciclopentanos, presentada por Eric V. Anslyn y Dennis A. Doughtery).
La teoría del estado de transición está también basada en la suposición de que los núcleos atómicos se comportan de acuerdo con la mecánica clásica.[8] Se supone que a no ser que los átomos o las moléculas colisionen con suficiente energía para formar la estructura de transición, o bien la reacción no ocurrirá. Sin embargo, de acuerdo con la mecánica cuántica, para cualquier barrera de energía de valor finito, hay una posibilidad de que las partículas puedan escapar por efecto túnel a través de la barrera. Con respecto a las reacciones químicas esto significa que hay una oportunidad de que las moléculas reaccionen incluso si no colisionan con suficiente energía para atravesar la barrera de energía.[9] Mientras se espera que este efecto sea insignificante para reacciones con energías de activación grandes, llega sin embargo a ser un fenómeno más importante para reacciones con barreras de energía relativamente bajas, ya que la probabilidad de efecto túnel aumenta cuanto menor es la altura de la barrera.
La teoría del estado de transición falla para algunas reacciones a alta temperatura. La teoría supone que el sistema reaccionante sobrepasará el punto de silla de energía más baja en la superficie de energía potencial. Recuérdese que el punto de mayor energía de este punto de silla se llama estado de transición. Mientras esta descripción es consistente para reacciones que ocurren a temperaturas relativamente bajas, a altas temperaturas, las moléculas se distribuyen en los modos de mayor energía vibracional; su movimiento se hace más complejo y las colisiones pueden conducir a estados de transición alejados de lo previsto por la teoría del estado de transición. Esta desviación de la teoría del estado de transición se observa incluso en la simple reacción de intercambio entre hidrógeno diatómico y un radical hidrógeno.[10]
Dadas estas limitaciones, se han propuesto varias alternativas a la teoría del estado de transición, como las que siguen.
Teoría generalizada del estado de transición[editar]
Cualquier forma de la teoría del estado de transición en las que el estado de transición no es exactamente un punto de silla es denominada teoría generalizada del estado de transición.
Teoría del estado de transición variacional microcanónica[editar]
Un desarrollo de la teoría del estado de transición en la que la superficie de separación se varía de modo que sea mínima la velocidad calculada para una energía fija. La expresiones de la velocidad obtenidas en el tratamiento microcanónico puede integrarse respecto de la energía, teniendo en cuenta la distribución estadística de los estados energéticos, para dar así las velocidades canónicas, o las térmicas.
Teoría del estado de transición variacional canónica[editar]
Un desarrollo de la teoría del estado de transición en la que la superficie de separación se varía de modo que sea mínima la constante de velocidad para una temperatura dada.
Teoría del estado de transición variacional canónica mejorada[editar]
Es una modificación de la teoría del estado de transición variacional canónica en la que, para energías por debajo de la energía umbral, la posición de la superficie de separación se toma para que coincida con la energía umbral microcanónica. Esto fuerza que las contribuciones de las constantes de velocidad sean nulas si están por debajo de la energía umbral. Una superficie de separación de compromiso es elegida entonces para así minimizar las contribuciones de la constante de velocidad por parte de los reactivos que tienen mayores energías.
Aplicaciones de la teoría del estado de transición[editar]
Algunas de las aplicaciones de esta teoría son la catálisis enzimática pues permite analizar relaciones de estructura, reactividad y especificidad,[11] o el modo de acción de la purina nucleósido fosforilasa.
Notas[editar]
- ↑ International Union of Pure and Applied Chemistry (IUPAC) Gold Book. Transition State Theory. http://goldbook.iupac.org/T06470.html (último acceso 3 de octubre de 2009).
- ↑ Truhlar, D. G.; Garrett, B. C.; Klippenstein, S. J., Current Status of Transition-State Theory. The Journal of physical chemistry 1996, 100, (31), 12771-12800.
- ↑ Laidler, K.; King, C, Development of transition-state theory. The Journal of physical chemistry 1983, 87, (15), 2657.
- ↑ Laidler, K.; King, C, A lifetime of transition-state theory. The chemical intelligencer 1998, 4, (3), 39.
- ↑ Laidler, K. J., Theories of Chemical Reaction Rates (McGraw-Hill Series in Advanced Chemistry). 1969; p. 234.
- ↑ Eric V. Anslyn and Dennis A. Dougherty. Transition State Theory and Related Topics. In Modern Physical Organic Chemistry University Science Books: 2006; pp 365-373.
- ↑ Laidler, K. J., Theories of Chemical Reaction Rates (McGraw-Hill Series in Advanced Chemistry). 1969; p. 234.
- ↑ Eyring, H.; Journal of Chemical Physics, 1935, 3, 107-115.
- ↑ Masel, R. Principles of Adsorption and Reactions on Solid Surfaces; Wiley, New York, 1996.
- ↑ Pineda, J. R.; Schwartz, S. D.; Philosophical Transactions of the Royal Society B 2006, 361, 1433-1438.
- ↑ Fersht, Alan: Estructura y mecanismo de los enzimas. Editorial Reverté.Barcelona, 1980.
Referencias[editar]
- Laidler, K.; King, C., Development of transition-state theory. The Journal of physical chemistry 1983, 87, (15), 2657
- Laidler, K., A lifetime of transition-state theory. The chemical intelligencer 1998, 4, (3), 39
- Eric V. Anslyn, Dennis A. Doughtery., Transition State Theory and Related Topics. In Modern Physical Organic Chemistry University Science Books: 2006; pp 365–373
- Schramm, VL., Enzymatic Transition States and Transition State Analog Design. Annual Review of Biochemistry 1998, 67, 693-720
- Schramm, V.L., Enzymatic Transition State Theory and Transition State Analogue Design. Journal of Biological Chemistry 2007, 282, (39), 28297-28300
- Radzicka, A.; Woldenden, R., Transition State and Multisubstrate Analog Inhibitors. Methods in Enzymology 1995, 249, 284-312
- Cleland, W.W., Isotope Effects: Determination of Enzyme Transition State Structure. Methods in Enzymology 1995, 249, 341-373
Véase también[editar]
Enlaces externos[editar]





















![{\displaystyle \mathrm {A} +\mathrm {B} \rightleftharpoons [\mathrm {AB} ]^{\ddagger }\to \mathrm {P} }](https://wikimedia.org/api/rest_v1/media/math/render/svg/6173f1d72ff092dc982c275f2b4cc3faf7934f97)
![{\displaystyle [AB_{\mathrm {r} }]^{\ddagger }={\frac {1}{2}}[AB]^{\ddagger }}](https://wikimedia.org/api/rest_v1/media/math/render/svg/718aea8ee732afe4cab765c29977124ad36b5b9e)
![{\displaystyle [AB_{\mathrm {l} }]^{\ddagger }={\frac {1}{2}}[AB]^{\ddagger }}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e5fcb4730a299151b8e90fe11b0e7cd933b45dad)

![{\displaystyle K^{\ddagger \ominus }={\frac {[AB]^{\ddagger }}{[A][B]}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c4b0d08053a799ac0a101205501c399240c53dab)
![{\displaystyle [\mathrm {AB} ]^{\ddagger }=K^{\ddagger \ominus }[\mathrm {A} ][\mathrm {B} ]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/675438f6f9190c4de1aaa0bc3f147b6c105c13db)
![{\displaystyle {\frac {d[P]}{dt}}=k^{\ddagger \ominus }[\mathrm {AB} ]^{\ddagger }=k^{\ddagger }K^{\ddagger }[A][B]=k[A][B]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b59cfe1307532faaffcccff0851fece2bf2f03be)






