Sistema de referencia no inercial

En mecánica newtoniana, un sistema de referencia no inercial es un sistema de referencia en el que no se cumplen las leyes del movimiento de Newton cuando sólo se consideran las fuerzas reales (no ficticias). Dado un sistema de referencia inercial, un segundo sistema de referencia será no inercial cuando describa un movimiento acelerado con respecto al primero. La aceleración del sistema no inercial puede deberse a:
- Un cambio en el módulo de su velocidad de traslación (aceleración lineal).
- Un cambio en la dirección de su velocidad de traslación (por ejemplo en un movimiento de giro alrededor de un sistema de referencia inercial).
- Un movimiento de rotación sobre sí mismo (véase figura 1).
- Una combinación de algunos de los anteriores.
Un ejemplo de sistema no inercial podría ser el correspondiente a un sistema de coordenadas "fijo en la Tierra", en el cual los movimientos de los cuerpos serían medidos respecto a puntos de la Tierra que estarían girando.
Un observador situado en un sistema de referencia no inercial deberá recurrir a fuerzas ficticias (tales como la fuerza de Coriolis o la fuerza centrífuga) para poder explicar los movimientos con respecto a dicho sistema de referencia. Estas fuerzas no existen realmente, en el sentido de que no son causadas directamente por la interacción con otro objeto, pero deberán introducirse si se quiere explicar el fenómeno según las leyes de Newton.
Por tanto, puede detectarse que un sistema de referencia dado es no inercial por sus violaciones de las leyes de Newton. Por ejemplo, la rotación de la Tierra se manifiesta por la rotación del vector de la gravedad que actúa sobre un péndulo de Foucault, que hace que el plano de oscilación del péndulo varíe respecto a su entorno.
Siendo rigurosos podría argumentarse que los sistemas de referencia inerciales no existen, o al menos no en nuestro entorno, pues la Tierra gira sobre sí misma y también alrededor del Sol, y este a su vez lo hace respecto al centro de la Vía Láctea. Sin embargo, con objeto de simplificar los problemas, normalmente se considerarán como inerciales sistemas que en realidad no lo son, siempre que el error que se cometa sea aceptable. Así, para muchos problemas resulta conveniente considerar la superficie de la Tierra como un sistema de referencia inercial.
Ejemplos de sistemas no inerciales[editar]
Ejemplo 1. Movimiento circular[editar]

Consideremos una plataforma giratoria dando vueltas con una velocidad angular , como la mostrada en la figura 2.
Un observador situado en el sistema de referencia no inercial (O', x', y', z') percibe que los objetos tienden a dirigirse hacia el exterior de la plataforma, con dirección radial. Para conseguir que un objeto situado sobre la plataforma se mantenga en su posición, lo ata con una cuerda a una barra vertical situada en el centro. Comprueba la tensión que adquiere la cuerda (T en la figura 2), y la justifica con la existencia de una fuerza con el mismo módulo que la tensión pero con dirección contraria, como la representada por en la figura 2 (fuerza ficticia conocida con el nombre de fuerza centrífuga).
Sin embargo, para un observador situado en el sistema de referencia (O, x, y, z) la única fuerza que interviene en el movimiento del objeto situado sobre la plataforma es la tensión de la cuerda (supongamos que no existe rozamiento con la plataforma). La tensión de la cuerda será la responsable de la aceleración centrípeta (de módulo ) que hará que el objeto describa una trayectoria circular, en lugar del movimiento rectilíneo que seguiría en ausencia de fuerzas, según lo que indican las leyes de Newton.
Así, únicamente el observador situado en el sistema de referencia no inercial necesitará fuerzas ficticias para explicar el movimiento.
Ejemplo 2. Ascensor[editar]

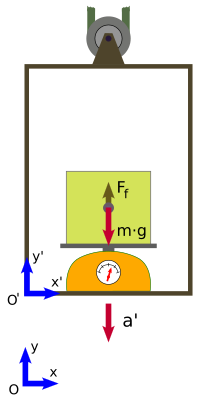
Consideremos ahora un ascensor descendiendo con una aceleración () respecto a un sistema de referencia inercial (figura 3). Un observador situado en el interior del ascensor y sin referencias exteriores cree estar en un sistema inercial dentro del campo gravitatorio terrestre. El observador deja caer un objeto de masa , desde una altura y estudia el movimiento respecto a un sistema de referencia situado en el suelo del ascensor.
El observador supone que el objeto está sometido únicamente a la aceleración de la gravedad, por lo que la posición del objeto será función del tiempo, y vendrá dada por la expresión siguiente (correspondiente a un movimiento uniformemente acelerado):
Y para el instante en el que el cuerpo llega al suelo del ascensor (y = 0):
Luego el tiempo que tarda en caer será:
El observador mide el tiempo que tarda el objeto en caer, pero para su sorpresa comprueba que este es mayor que el que se obtendría con la fórmula anterior. Por tanto, la aceleración tiene que ser más pequeña que la de la gravedad. Para justificarlo piensa que debe haber otra fuerza (fuerza ficticia) que se oponga al movimiento, de forma que:
siendo la aceleración aparente del objeto para el observador que realiza la medición del tiempo.
Por tanto, la expresión para obtener el tiempo correcto sería:
Sin embargo, un observador situado en el sistema de referencia inercial no tendrá que recurrir a ninguna fuerza ficticia para explicar el movimiento. La posición del suelo del ascensor (ver figura 3) vendría dada por:
Y la del objeto:
En el instante en que el objeto llega al suelo del ascensor, la posición del objeto y la del suelo de ascensor coinciden, por lo que . Es decir:
De donde se obtiene:
que coincide con la expresión que se obtuvo para el sistema de referencia no inercial con el uso de la fuerza ficticia.
También podríamos observar una violación de las leyes de Newton, si situáramos una masa conocida en una báscula fijada al suelo del ascensor. En este caso el peso medido por la báscula sería inferior al peso real. Su peso aparente sería igual al peso real menos la fuerza ficticia (figura 4). Es decir:
Razonamientos similares pueden realizarse para el caso en el que el ascensor estuviera ascendiendo con una aceleración . La diferencia está en que la fuerza ficticia tendría dirección contraria (estaría dirigida hacia abajo).
Desarrollo formal en mecánica newtoniana[editar]

Sean S y S' dos sistemas de referencia como los mostrados en la figura 5. Consideremos que S sea un sistema fijo y que S' sea un sistema de referencia no inercial con movimiento acelerado respecto al primero (translación y/o rotación).
Se puede demostrar[1][2] que las derivadas temporales de un vector cualquiera respecto a los dos sistemas de referencia anteriores, S y S', están relacionadas por la expresión:
(1)
donde los subíndices S y S' representan el sistema de referencia con respecto al cual se realiza la derivación, y es la velocidad angular del sistema de referencia S' respecto al sistema de referencia S.
La ecuación (1) nos va a ser de utilidad para obtener la ecuación correspondiente a la segunda ley de Newton para el sistema de referencia no inercial S'. Esto será lo que hagamos a continuación.
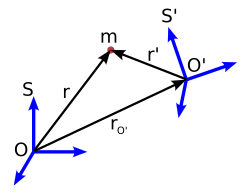
Sea un objeto de masa m, situado respecto a los sistemas de referencia S y S', según se muestra en la figura 6. Los vectores de posición están relacionados por la ecuación:
(2)
Derivando la ecuación (2) respecto al tiempo y aplicando (1), obtenemos:
(3)
que puede escribirse también como la ecuación que relaciona las velocidades:
(4)
Volviendo a derivar y aplicando de nuevo la ecuación (1), obtenemos la expresión:
que puede reescribirse como:
con lo que la aceleración del objeto en el sistema de referencia no inercial será:
(5)
Y multiplicando por la masa se obtiene finalmente la segunda ley de Newton para el sistema de referencia no inercial:
(6)
Por otro lado, la expresión para la segunda ley de Newton en el sistema de referencia inercial es:
(7)
Comparando las ecuaciones (6) y (7) se observa que para el caso del sistema referencia no inercial han aparecido cuatro términos, conocidos como fuerzas ficticias por no deberse a la interacción del objeto con otros cuerpos:
1 : es conocido como fuerza de Coriolis
2 : se conoce como fuerza centrífuga
3 : es una fuerza que solo estará presente en los sistemas con aceleración angular
4 : es debida a la aceleración del origen de S' respecto a S.
Los cuatro términos aparecen con signo negativo, y corresponden a aceleraciones sufridas por el sistema S', con centro en O', respecto al sistema inercial S, con centro en O, y cada uno de ellos compensa una forma de aceleración sufrida por el sistema S' respecto a S. Esto es, las fuerzas ficticias son la compensación de las fuerzas necesarias para que el sistema S' este acelerado respecto a S.
Desarrollo formal en mecánica relativista[editar]
La mecánica relativista considera sistemas mecánicos moviéndose en un espacio-tiempo plano o espacio de Minkowski. En dicha teoría cualquier sistema de coordenadas admisible es válido para representar el movimiento.
Sin embargo, la simple generalización de las leyes de Newton no será válida en cualquiera de esos sistemas a menos que sean sistemas de coordenadas galileanas en las que los símbolos de Christoffel se anulen. El equivalente relativista de la segunda ley de Newton para un sistema de referencia arbitrario será:
,
donde:
- es la masa de la partícula,
- son las coordenadas de la partícula,
- es el tiempo propio de la partícula,
- son los símbolos de Christoffel asociados al sistema de coordenada, y
- es la cuadrifuerza que actúa sobre la partícula.
En un sistema de referencia inercial relativista, dado que para ese sistema, se tendrá que:
,
que tiene la forma de segunda ley de Newton.
Véase también[editar]
Referencias[editar]
- ↑ Di Bartolo, Cayetano (2004)). «Mecánica Clásica 1» (PDF). Tema 1: Leyes de Newton. Referenciales no inerciales (Departamento de Física. Universidad Simón Bolívar). Archivado desde el original el 19 de febrero de 2009. Consultado el 22 de noviembre de 2007.
- ↑ Barrachina, Raúl Oscar (2004). «Apuntes de Mecánica Clásica» (PDF). Capítulo 3: Sistemas de coordenadas rotantes (Instituto Balseiro. Argentina).
Bibliografía[editar]
- French A. P.: Mecánica Newtoniana, MIT Physics Course, Ed. Reverté, 1978.
- Martínez Benjamín, J. J.: Mecánica Newtoniana. Edicions UPC, 2001.
- Marion, J. B.: Dinámica Clásica de las Partículas y Sistemas. Ed. Reverté, Barcelona, 1981.
- Kittel y otros: Mecánica, Berkeley Physics Course (vol. I). Segunda edición. Ed. Reverté. Barcelona, 1992.
- Goldstein, H.: Mecánica Clásica, Ed. Reverté (20 ed.). 1992.
Enlaces externos[editar]
- El problema de los sistemas de referencia. Manuel Alonso Sánchez
- Nivel avanzado
- Mecánica Clásica. Cayetano Di Bartolo.
- Apuntes de Mecánica Clásica. Instituto Balseiro.




















![{\displaystyle \left[{\frac {d{\vec {b}}}{dt}}\right]_{S}=\left[{\frac {d{\vec {b}}}{dt}}\right]_{S'}+{\vec {\omega }}_{S'|S}\times {\vec {b}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/137accc6dfa8e83ca9f48e2890fcdd99083f069b)


![{\displaystyle \left[{\frac {d{\vec {r}}}{dt}}\right]_{S}=\left[{\frac {d{\vec {r\,'}}}{dt}}\right]_{S}+\left[{\frac {d{\vec {r}}_{O'}}{dt}}\right]_{S}=\left[{\frac {d{\vec {r\,'}}}{dt}}\right]_{S'}+{\vec {\omega }}_{S'|S}\times {\vec {r\,'}}+\left[{\frac {d{\vec {r}}_{O'}}{dt}}\right]_{S}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/a5d7d32f6d0e91fcfb29f183f0ba4eaf6b8466b3)

![{\displaystyle \left[{\frac {d{\vec {v}}}{dt}}\right]_{S}=\left[{\frac {d{\vec {v\,'}}}{dt}}\right]_{S}+\;{\frac {d{\vec {\omega }}_{S'|S}}{dt}}\times {\vec {r\,'}}\;+\;{\vec {\omega }}_{S'|S}\times \left[{\frac {d{\vec {r\,'}}}{dt}}\right]_{S}+\left[{\frac {d{\vec {v}}_{O'}}{dt}}\right]_{S}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/4fa71461379ce645192c18d3865e956e1f6f6d5e)
![{\displaystyle =\left[{\frac {d{\vec {v\,'}}}{dt}}\right]_{S'}+\;{\vec {\omega }}_{S'|S}\times {\vec {v\,'}}\;+\;{\frac {d{\vec {\omega }}_{S'|S}}{dt}}\times {\vec {r\,'}}\;+\;{\vec {\omega }}_{S'|S}\times \left(\left[{\frac {d{\vec {r\,'}}}{dt}}\right]_{S'}+{\vec {\omega }}_{S'|S}\times {\vec {r\,'}}\right)+\left[{\frac {d{\vec {v}}_{O'}}{dt}}\right]_{S}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d558c97dc5650d561d603d1a3698029e837a3db6)















