Mecanismo de cuatro barras

Mecanismo de cuatro barras.

Animación de un mecanismo de cuatro barras

En ingeniería mecánica un mecanismo cuatro barras o cuadrilátero articulado es un mecanismo formado por tres barras móviles y una cuarta barra fija (por ejemplo, el suelo), unidas mediante nudos articulados (unión de revoluta o pivotes). Las barras móviles están unidas a la fija mediante pivotes. Usualmente las barras se numeran de la siguiente manera:

• Barra 2. Barra que proporciona movimiento al mecanismo.
• Barra 3. Barra superior.
• Barra 4. Barra que recibe el movimiento.
• Barra 1. Barra imaginaria que vincula la unión de revoluta de la barra 2 con la unión de revoluta de la barra 4 con el suelo.

Ley de Grashof

La Ley de Grashof es una fórmula utilizada para analizar el tipo de movimiento que hará el mecanismo de cuatro barras: para que exista un movimiento continuo entre las barras, la suma de la barra más corta y la barra más larga no puede ser mayor que la suma de las barras restantes.

                               S + L ≤ P + Q

Donde: S = longitud del eslabón más corto L = longitud del eslabón más largo P = longitud de un eslabón restante Q = longitud de otro eslabón restante

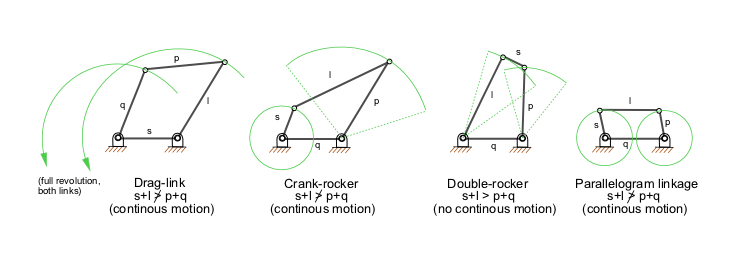
Análisis cinemático del mecanismo de cuatro barras

Una vez que el diseño (síntesis) de un mecanismo ha sido realizado, este debe ser analizado. El objetivo del análisis cinemático es determinar las posiciones, velocidades y aceleraciones de todas las partes en movimiento en un mecanismo.

Se necesitan conocer las aceleraciones lineales y angulares. Para calcular dichas aceleraciones, debemos hallar antes las velocidades lineales y angulares. Y antes de calcular velocidades se calculan primero las posiciones lineales y angulares.

Todo el proceso anterior se realiza para pequeños incrementos de valor de las variables de entradas (es decir de los grados de libertad). Si la entrada es un ángulo θ, el incremento puede ser de 1° cada vez. Si la entrada es una distancia x, el incremento puede ser de 1 mm (esto es a juicio del ingeniero) cada vez.

Todos los cálculos deben ser hechos con el apoyo de un programa de computadora, debido a la necesidad de resolver una gran cantidad de ecuaciones, un número considerable de veces (por ejemplo, cuando θ es dada, se pueden hacer 360 veces el cálculo).

A continuación se describe el análisis de posición.

Análisis de posición

Por mediciones físicas fácilmente se pueden tener las longitudes de las barras 1, 2, 3, 4. Ya que la barra 1 es estacionaria, su ángulo es fijo. Se dice que el ángulo de la barra 2 con respecto a la horizontal es una variable controladora. Por lo tanto, las incógnitas serán los ángulos de las barras 3 y 4.

Ecuación vectorial:

${\bar {l}}_{1}+{\bar {l}}_{2}+{\bar {l}}_{3}+{\bar {l}}_{4}={\bar {0}}$

$l_{1}\cos \theta \ _{1}i+l_{1}\sin \theta \ _{1}j+l_{2}\cos \theta \ _{2}i+l_{2}\sin \theta \ _{2}j+l_{3}\cos \theta \ _{3}i+l_{3}\sin \theta \ _{3}j+l_{4}\cos \theta \ _{4}i+l_{4}\sin \theta \ _{4}j={\bar {0}}$

Separando las ecuaciones en dirección "i" y dirección "j"

Ecuación en "i": $l_{1}\cos \theta \ _{1}+l_{2}\cos \theta \ _{2}+l_{3}\cos \theta \ _{3}+l_{4}\cos \theta \ _{4}=0$
Ecuación en "j": $l_{1}\sin \theta \ _{1}+l_{2}\sin \theta \ _{2}+l_{3}\sin \theta \ _{3}+l_{4}\sin \theta \ _{4}=0$

Como se conocen el ángulo de la barra 2 y el ángulo de la barra 1, es posible simplificar realizando los siguientes cambios de variable:

$A=l_{1}\cos \theta \ _{1}+l_{2}\cos \theta \ _{2}$

$B=l_{1}\sin \theta \ _{1}+l_{2}\sin \theta \ _{2}$

Con lo cual queda el sistema de ecuaciones como:

$A+l_{3}\cos \theta \ _{3}=-l_{4}\cos \theta \ _{4}$

$B+l_{3}\sin \theta \ _{3}=-l_{4}\sin \theta \ _{4}$

Al elevar los términos al cuadrado y sumar ambas ecuaciones, teniendo en cuenta que $\cos ^{2}\theta \ +\sin ^{2}\theta \ =1$, se simplifica de la siguiente manera:

$A^{2}+2Al_{3}\cos \theta \ _{3}+B^{2}+2Bl_{3}\sin \theta \ _{3}+l_{3}^{2}=l_{4}^{2}$

$A\cos \theta \ _{3}+B\sin \theta \ _{3}={\frac {l_{4}^{2}-l_{3}^{2}-A^{2}-B^{2}}{2l_{3}}}$

Es posible volver a simplificar realizando el siguiente cambio de variable:

$C={\frac {l_{4}^{2}-l_{3}^{2}-A^{2}-B^{2}}{2l_{3}}}$

Utilizando las identidades trigonométricas

$\sin \theta \ ={\frac {2\tan {\frac {1}{2}}\theta \ }{1+\tan ^{2}{\frac {1}{2}}\theta \ }}$, $\cos \theta \ ={\frac {1-\tan ^{2}{\frac {1}{2}}\theta \ }{1+\tan ^{2}{\frac {1}{2}}\theta \ }}$

y sustituyendo las identidades en la ecuación:

${\frac {A\left(1-\tan ^{2}{\frac {1}{2}}\theta \ _{3}\right)+B\left(2\tan {\frac {1}{2}}\theta \ _{3}\right)}{1+\tan ^{2}{\frac {1}{2}}\theta \ _{3}}}=C$

se obtiene una ecuación cuadrática. Al usar la fórmula general para resolver el sistema se obtiene:

$\tan {\frac {1}{2}}\theta \ _{3}={\frac {B\pm {\sqrt {A^{2}+B^{2}-C^{2}}}}{C+A}}$

El valor para el ángulo de la barra 3 es el siguiente:

$\theta \ _{3}=2\ tan^{-1}\left({\frac {B\pm {\sqrt {A^{2}+B^{2}-C^{2}}}}{C+A}}\right)$

Para obtener el valor del ángulo de la barra 4 es el mismo procedimiento, definiendo el siguiente cambio de variable:

$D={\frac {l_{3}^{2}-l_{4}^{2}-A^{2}-B^{2}}{2l_{4}}}$

El valor del ángulo de la barra 4 resulta:

$\theta \ _{4}=2\ tan^{-1}\left({\frac {B\mp {\sqrt {A^{2}+B^{2}-D^{2}}}}{D+A}}\right)$

NOTA: los dos valores que se pueden obtener para cada ángulo representan las diferentes configuraciones del sistema.

Análisis de velocidad

Este mecanismo debe analizarse mediante el método de la velocidad relativa

Datos de entrada

• El único dato referido a velocidad que se conoce en un mecanismo de cuatro barras es la velocidad angular de la barra 2.
• Mediante un análisis previo de posición se conoce la información de las barras.

Para el análisis se procederá a buscar la velocidad del punto B (unión de la barra 3 y 4). Para este punto existen dos trayectorias posibles: desde $O_{2}\,$ hasta B y desde $O_{4}\,$ hasta B. Para comenzar se define la velocidad de B con respecto a la barra 4

${\bar {V}}_{B}={\bar {\omega }}\ _{4}\times \ {\bar {l}}_{4}=\omega \ _{4}l_{4}\cos \theta \ _{4}{\hat {j}}-\omega \ _{4}l_{4}\sin \theta \ _{4}{\hat {i}}$

Ahora se definirá la velocidad del punto B con respecto a la otra trayectoria.

${\bar {V}}_{B}={\bar {V}}_{B|A}+{\bar {V}}_{A}={\bar {\omega }}\ _{3}\times \ {\bar {l}}_{3}+{\bar {\omega }}\ _{2}\times \ {\bar {l}}_{2}$

${\bar {V}}_{B}=\omega \ _{3}l_{3}\cos \theta \ _{3}{\hat {j}}-\omega \ _{3}l_{3}\sin \theta \ _{3}{\hat {i}}+\omega \ _{2}l_{2}\cos \theta \ _{2}{\hat {j}}-\omega \ _{2}l_{2}\sin \theta \ _{2}{\hat {i}}$

Igualando las ecuaciones para ${\bar {V}}_{B}\,$ y separando los componentes, se obtiene un sistema de dos ecuaciones con dos incógnitas.

${\hat {i}}\Rightarrow -\omega \ _{4}l_{4}\sin \theta \ _{4}=-\omega \ _{3}l_{3}\sin \theta \ _{3}-\omega \ _{2}l_{2}\sin \theta \ _{2}$

${\hat {j}}\Rightarrow \omega \ _{4}l_{4}\cos \theta \ _{4}=\omega \ _{3}l_{3}\cos \theta \ _{3}+\omega \ _{2}l_{2}\cos \theta \ _{2}$

Análisis de aceleración

Este mecanismo debe analizarse mediante el método de aceleración relativa.

Simuladores gratuitos

• Simulador de 4 Barras Gráfica la posición, velocidad y aceleración. (Solo para windows)
• Código fuente Gráfica la posición y curva de acoplador. (Incluye código fuente en c++ con Qt5 y un binario precompilado para windows)

Referencias

Norton, R. (1995). Diseño de Maquinaria. México: McGraw Hill.

Véase también

• Mecanismo
• Ley de Grashof
• Teoría de Burmester

• Datos: Q2102938
• Multimedia: Four-bar linkage / Q2102938