Leyes de Kepler

Esquema de la Primera Ley de Kepler.

Esquema de la Segunda Ley de Kepler.

Las leyes de Kepler fueron enunciadas por Johannes Kepler para explicar el movimiento de los planetas en sus órbitas alrededor del Sol. Aunque él no las enunció en el mismo orden, en la actualidad las leyes se numeran como sigue:

• Primera Ley (200): Todos los planetas se desplazan alrededor del Sol describiendo órbitas elípticas, estando el Sol situado en uno de los focos.

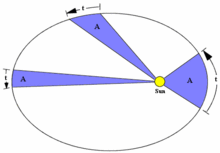
• Segunda Ley (1609): El radio vector que une el planeta y el Sol barre áreas iguales en tiempos iguales.

La ley de las áreas es equivalente a la constancia del momento angular, es decir, cuando el planeta está más alejado del Sol (afelio) su velocidad es menor que cuando está más cercano al Sol (perihelio). En el afelio y en el perihelio, el momento angular L es el producto de la masa del planeta, su velocidad y su distancia al centro del Sol.

$L=m\cdot r_{1}\cdot v_{1}=m\cdot r_{2}\cdot v_{2}\,$

• Tercera Ley (1618): Para cualquier planeta, el cuadrado de su período orbital (tiempo que tarda en dar una vuelta alrededor del Sol) es directamente proporcional al cubo de la distancia media con el Sol.

${\frac {P^{2}}{r^{3}}}=K=constante$

donde, P  es el periodo orbital, r  la distancia media del planeta con el Sol y K  la constante de proporcionalidad.

Estas leyes se aplican a otros cuerpos astronómicos que se encuentran en mutua influencia gravitatoria como el sistema formado por la Tierra y la Luna.

Formulación de Newton de la tercera ley de Kepler

Kepler dedujo sus leyes a partir de observaciones astronómicas precisas obtenidas por Tycho Brahe y, aunque sabía que explicaban el movimiento planetario observado, no entendía las razones de este comportamiento. La presentación de Kepler incorporaba una gran cantidad de detalles e incluso especulaciones metafísicas. Fue Isaac Newton quien extrajo de los escritos de Kepler la formulación matemática precisa de las leyes. Newton fue capaz de relacionar estas leyes con sus propios descubrimientos, dando un sentido físico preciso a leyes empíricas. El estudio de Newton de las leyes de Kepler condujo a su formulación de la ley de la gravitación universal.

La formulación matemática de Newton de la tercera ley de Kepler es:

$P^{2}={\frac {4\pi ^{2}}{G(m_{1}+m_{2})}}a^{3}$

donde, P  es el periodo orbital, a  el semieje mayor de la órbita, m₁ y m₂  las masas del cuerpo central y el cuerpo orbitante respectivamente y G  una constante denominada Constante de gravitación universal cuyo valor marca la intensidad de la interacción gravitatoria y el sistema de unidades a utilizar para las otras variables de esta expresión.