Discusión:Leyes de Kepler

Hay que explicar mejor esto:

cuanto mayor es la distancia media de un planeta al sol, más tiempo tarda en completar su órbita

porque no aclara al profano (todo aquél que se líe con "periodos orbitales" "semiejes mayores" de la órbita y quizá hasta con cuadrados y cubos) si se dice algo más que una órbita más grande se tarda más en recorrer, o si la velocidad es menor o qué.

Hay que explicar mejor TODO, está flojísimo todo. Juancitox 13:08 23 ene 2012 (UTC)

Semieje menor

En la tercera ley, "a" es el semieje mayor, no la distancia de la tierra al sol

--Cidel (discusión) 18:39 14 abr 2010 (UTC)

... y semieje mayor

La distancia media de la Tierra al Sol (o, de forma más general, de un planeta que describe una elipse a su estrella) coincide con el semieje mayor de la órbita. Si llamamos a al "semieje mayor" de la elipse, es decir, a la mitad del "eje mayor" de la elipse, y r₁ y r₂ a las distancias desde el foco en el que se encuentra la estrella hasta cada uno de los extremos del "eje mayor", o lo que es lo mismo, al afelio y al perihelio se cumple que a es precisamente:

a = (r₁ + r₂)/2

es decir, coincide con la distancia media. Una sencilla imagen como esta [1] es bastante clarificadora (la excentricidad de la órbita está exagerada a propósito). Coincido en la opinión de que el artículo está un poco flojo y propongo introducir esta apreciación sobre la distancia media, así como la introducción de una figura más clara (o dos, una para explicar la segunda ley y otra para señalar distancias y vectores en la órbita). --Andesito (discusión) 19:53 1 feb 2019 (UTC)

que tiene que ver la tonta imagen de la estampilla con lo que en realidad se intenta explicar!!

• Todo, estimada IP. Todo. Emilio - Fala-me 12:21 31 may 2010 (UTC)
  • A mí me parece innecesaria Juancitox 13:04 23 ene 2012 (UTC)

Formulación de Newton de la tercera ley de Kepler

Si el título menciona solo de la tercera Ley de Kepler, por qué se habla de historia y por qué se vuelven a enunciar las leyes? Además, con la formulación de Newton se pueden deducir las Leyes de Kepler Juancitox 15:41 26 nov 2011 (UTC)

Algunas precisiones

En el artículo la formulación se obtiene, en primer lugar para órbitas circulares, lo que no se especifica.

A continuación se dice que C en realidad no es constante, pero la expresión que se da muestra que es constante aunque un poco distinta a la anterior:

${\frac {T^{2}}{a^{3}}}\ (M+m)={\frac {4\pi ^{2}}{G}}$

Si M y m son constantes (suposición tan buena como que M es constante) el resultado es que

${\frac {T^{2}}{a^{3}}}={\frac {4\pi ^{2}}{G(M+m)}}$

es también una constante. Solo que a es el semieje mayor de La órbita alrededor del centro de masas. --Mcovas (discusión) 07:47 21 ago 2021 (UTC)

¿Artículo vandalizado?

He observado que aparece el término "LINUX" para referirse al semieje mayor de la órbita. ¿Se ha elegido ese término a propósito o es fruto del vandalismo?

¿Cual es el valor de K?

Debería incluirse. No lo encuentro por ningun otro lado en internet (en unidades SI). Tampoco se incluye en el articulo en ningun sistema de unidades. R= EL valor de K es todo numero entero...

¿Radio vector?

Se enuncia la segunda ley así: "El radio vector que une un planeta y el Sol barre áreas iguales en tiempos iguales" Me molesta el termino "radio vector", se lo que es un vector, y un sistema de coordenada radiales. Pero "radio vector" es la primera vez que lo veo. Mas allá de mi brutalidad / erudición creo que el termino complica al que se acerca por primera vez a esto. En ingles se habla de "line segment", que traduciría por segmento, o segmento de recta. En internet en algunos sitios hablan de radio vector y en otros de la recta que une al planeta con el sol. https://anuars.wordpress.com/tag/segunda-ley-de-kepler-explicacion/ https://www.windows2universe.org/the_universe/uts/kepler2.html&lang=sp Por eso propongo cambiar el termino radio vector por segmento de recta. La ley quedaría así: "El segmento de recta que une un planeta y el Sol barre áreas iguales en tiempos iguales".

Marcelo

El término radio vector se usa en geometría, en el estudio de las cónicas. En la elipse y en la hiperbola los radios vectores de un punto son los segmentos que unen los focos con dicho punto. Es un término perfectamente aceptado en geometría y se puede aplicar a una órbita elíptica describir el movimiento planetario entendiendo que un planeta no es un punto, que el foco es el centro de masas, etc --Mcovas (discusión) 07:58 21 ago 2021 (UTC)

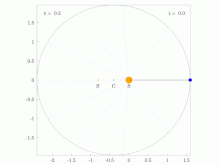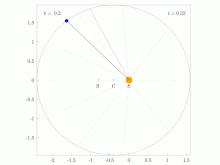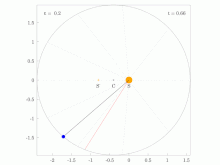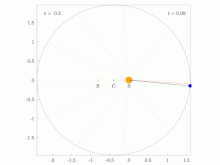
Animations demonstrating Kepler's Second Law of Planetary Motion.

There is an animated figure on the English version of this page which I made which the shows motion of planets orbiting with various eccentricities around a star and may be of use. The animated gifs are individually viewable at

https://commons.wikimedia.org/wiki/File:Circular_orbit_of_planet_with_(eccentricty_of_0.0).gif

https://commons.wikimedia.org/wiki/File:Ellipitical_orbit_of_planet_with_an_eccentricty_of_0.2.gif

https://commons.wikimedia.org/wiki/File:Ellipitical_orbit_of_planet_with_an_eccentricty_of_0.5.gif

https://commons.wikimedia.org/wiki/File:Ellipitical_orbit_of_planet_with_an_eccentricty_of_0.8.gif

The code to produce the table is here (see edit mode):

Orbits of planets with varying eccentricities. The red ray rotates at a constant angular velocity and with the same orbital time period as the planet, $T=1$. S: Sun at the primary focus, C: Centre of ellipse, S': The secondary focus. In each case, the area of all sectors depicted is identical.

Low	High
Planet orbiting the Sun in a circular orbit (e=0.0)	Planet orbiting the Sun in an orbit with e=0.5
Planet orbiting the Sun in an orbit with e=0.2	Planet orbiting the Sun in an orbit with e=0.8

Mkwadee (discusión) 19:25 20 dic 2022 (UTC)

Bueno, el asunto es que Urbano Leverrier , a partir de calculos teóricos predice la posición de Neptuno que Galle confirma .

Bueno, el asunto es que Urbano Leverrier , a partir de calculos teóricos predice la posición de Neptuno que Galle confirma en el observatorio de Berlin Marko Lambda (discusión) 02:57 1 ago 2023 (UTC)