Ley Mu
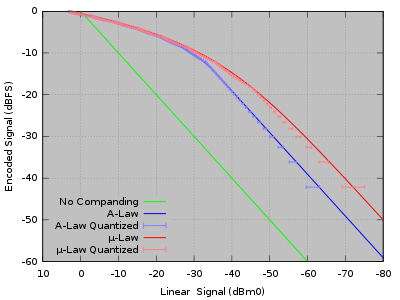
El algoritmo Ley μ o Ley Mu es un sistema de cuantificación logarítmica de una señal de audio, usado en el campo de comunicaciones telefónicas. Es utilizado principalmente para audio de voz humana dado que explota las características de ésta. El nombre de Ley μ proviene del término original inglés "µ-law", que usa la letra griega µ (Mu). Este sistema de codificación es usado en Estados Unidos y Japón, mientras que en Europa y en el resto del mundo se utiliza un sistema muy parecido llamado ley A. Forma parte de la Recomendación G.711 de la UIT-T.[1]
Tipos de algoritmos
[editar]Existen dos tipos de algoritmos de Ley-Mu: una versión analógica y otra digital cuantizada.
Versión analógica
[editar]Para una entrada determinada, la ecuación para la codificación según la Ley Mu es:[2]
en la cual:
- : (8 bits) es el estándar usado en Norteamérica y Japón.
- : es la función signo.
En el receptor, la expansión analógica viene dada por la inversa de la ecuación anterior:
Versión digital
[editar]La Ley Mu, en su forma cuantificada digital, está definida en la Recomendación G.711. El comportamiento de la cuantificación se aproxima al de la codificación analógica mediante 16 segmentos rectilíneos, pero como los segmentos que pasan por el origen son colineales, éstos se consideran uno solo, quedando en total 15 segmentos, nombrándose éstos como 0, ±1 hasta ±7. Digitalmente, es aplicada una cuantificación no uniforme (logarítmica) a la señal original, en la cual existen pequeños pasos de cuantificación para los valores pequeños de amplitud y pasos de cuantificación grandes para los valores grandes de amplitud. Sin embargo, esta recomendación es poco clara acerca de cómo codificar los valores en el límite de un rango (por ejemplo, si a +31 le corresponde el número hexadecimal 0xEF o el 0xF0). Sin embargo, la Recomendación G.191[3] ofrece un ejemplo de código en lenguaje C para un codificador de Ley Mu lo que proporciona la codificación de la tabla adjunta a esta sección.[4] En este caso, cada muestra de señal de audio telefónico se convierte a su equivalente a 14 bits: un bit de signo "S" (0=negativo y 1=positivo) más 13 bits de magnitud. Antes de la determinación del segmento de cada muestra, el bit de signo se retira y se aplica un desplazamiento de 33 unidades al código lineal por lo que la mayor muestra es de 8192-33=8159 y la resolución es de 2/8159. Este desplazamiento permite convertir los extremos de cada segmento en números que son potencias de 2 lo que simplifica la determinación de segmento y de paso de cuantificación.[4] Finalmente, el conjunto de bits se comprime, sin afectar al bit de signo, como se indica seguidamente en la tabla:
| Codificación binaria de Ley Mu | ||
| Segmento | Código lineal binario de 14 bits | Código comprimido de 8 bits |
| 0 | S00000001ABCDX | S000ABCD |
| ±1 | S0000001ABCDXX | S001ABCD |
| ±2 | S000001ABCDXXX | S010ABCD |
| ±3 | S00001ABCDXXXX | S011ABCD |
| ±4 | S0001ABCDXXXXX | S100ABCD |
| ±5 | S001ABCDXXXXXX | S101ABCD |
| ±6 | S01ABCDXXXXXXX | S110ABCD |
| ±7 | S1ABCDXXXXXXXX | S111ABCD |
Durante la compresión, como se observa en la tabla, se descartan los bits menos significativos de las señales grandes. La cantidad de estos bits es representada por tres bits, los cuales pasan al código comprimido después del bit de signo "S" junto con cada uno de los pasos de cuantificación indicados como "ABCD". El número de 3 bits representa cada uno de los segmentos en que se divide la curva . Antes de la transmisión de cada código comprimido, este es invertido, ya que las señales de baja amplitud tienden a ser más numerosas que las grandes. La inversión de los bits incrementa la densidad de los pulsos positivos en el medio de transmisión, lo que mejora el desempeño de la circuitería.[4] La descompresión del código recibido permite obtener la siguiente tabla:
| Decodificación binaria de Ley Mu | |
| Código Comprimido de 8 bits | Código Lineal de salida |
| S000ABCD | S00000001ABCD1 |
| S001ABCD | S0000001ABCD10 |
| S010ABCD | S000001ABCD100 |
| S011ABCD | S00001ABCD1000 |
| S100ABCD | S0001ABCD10000 |
| S101ABCD | S001ABCD100000 |
| S110ABCD | S01ABCD1000000 |
| S111ABCD | S1ABCD10000000 |
El rango dinámico (RD) de la Ley Mu es la relación en decibelios de la mayor amplitud cuantificable y de la amplitud más pequeña que ocupa el primer segmento de la curva . Como la máxima magnitud es de 8159 y el valor mínimo de cuantificación del primer segmento es 31 (los cinco 5 bits menos significativos del primer renglón en la primera tabla), entonces el rango dinámico (RD) se calcula así:[5]
que es algo menor que el calculado para la Ley A.
Características básicas de la Ley μ
[editar]- Es un algoritmo estandarizado, definido en el estándar ITU-T G.711
- Tiene una complejidad muy baja
- No introduce prácticamente retardo algorítmico (dada su baja complejidad)
- Es adecuado para sistemas de transmisión TDM
- No es adecuado para la transmisión por paquetes
- Factor de compresión aproximadamente de 2:1
Digitalmente, el algoritmo ley μ es un sistema de compresión con pérdida en comparación con la codificación lineal normal. Esto significa que al recuperar la señal, ésta no será exactamente igual a la original.
Planteamiento del algoritmo
[editar]Este algoritmo se utiliza principalmente para la codificación de voz humana, ya que su funcionamiento explota las características de esta. Las señales de voz están formadas en gran parte por amplitudes pequeñas, ya que son las más importantes para la percepción del habla, por lo tanto estas son muy probables. En cambio, las amplitudes grandes no aparecen tanto, por lo tanto tienen una probabilidad de aparición muy baja.
En el caso de que una señal de audio tuviera una probabilidad de aparición de todos los niveles de amplitud por igual, la cuantificación ideal sería la uniforme, pero en el caso de la voz humana esto no ocurre, estadísticamente aparecen con mucha más frecuencia niveles bajos de amplitud.
El algoritmo de Ley Mu explota el factor de que los altos niveles de amplitud no necesitan tanta resolución como los bajos. Por lo tanto, si se suministran más niveles de cuantificación a las bajas amplitudes y menos a las altas se consigue más resolución, un error de cuantificación inferior y por lo tanto una relación señal/ruido (SNR) superior que si se hiciera directamente una cuantificación uniforme para todos los niveles de la señal.
Esto provoca que si para una determinada SNR se necesitan, por ejemplo, 16 bits usando una cuantificación uniforme, para la misma SNR usando la codificación Ley μ se requieren 8 bits, dado que el error de cuantificación es menor.
Implementación
[editar]Existen tres formas de implementar el algoritmo de la Ley Mu:
- Analógica: Usa un amplificador de ganancia no-lineal para lograr la compansión completamente en el dominio analógico.
- Conversión de Analógico a Digital No lineal: En este caso, la amplificación es lineal y se usaría un convertidor analógico-digital con niveles desiguales de cuantificación que se ajustan a la tabla descrita. Sin embargo, construir tal convertidor es difícil.[6]
- Digital: La señal de entrada es muestreada y cuantificada de modo lineal, y el código lineal es comprimido convirtiendo el código de 12 o 14 bits en 8 bits como se indica en la tabla de este artículo. En el extremo receptor se lleva a cabo la expansión digital respectiva.[6]
Funcionamiento
[editar]El algoritmo de Ley Mu basa su funcionamiento en un proceso de compresión y expansión llamado compansión. Se aplica una compresión/expansión de las amplitudes y posteriormente una cuantificación uniforme. Las amplitudes de la señal de audio pequeñas son expandidas y las amplitudes más elevadas son comprimidas.
El funcionamiento se basa en que cuando una señal pasa a través de un compansor, el intervalo de las amplitudes pequeñas de entrada es representado por un intervalo de cuantificación más grande en la salida, y el intervalo de las amplitudes más elevadas pasa a ser representado en un intervalo de cuantificación más pequeño en la salida, tal como se muestra en la figura anexa:

Esta figura muestra que los valores de entrada (línea horizontal) contenidos en el intervalo [-0.2,+0.2] (amplitudes pequeñas) están representados en la salida (línea vertical) en el intervalo [-0.6,0.6], por lo que se constata que hay una expansión digital. Por otra parte, los valores de entrada contenidos en los intervalos [-1,-0,6] y [+0.6,+1] son representados en la salida en los intervalos [-0.9,-1] y [+0.9,+1], lo que representa una compresión digital.
Digitalmente, este esquema es equivalente a aplicar una cuantificación no uniforme (logarítmica) a la señal original, en la cual existen pequeños pasos de cuantificación para los valores pequeños de amplitud y pasos de cuantificación grandes para los valores grandes de amplitud. Para recuperar la señal en el destino, se aplica la función inversa.
Por lo tanto, la implementación del sistema consiste en aplicar a la señal de entrada una función logarítmica y una vez procesada, realizar una cuantificación uniforme. Es lo mismo que decir que el paso de cuantificación sigue una función del tipo logarítmico.
Véase también
[editar]Referencias
[editar]- ↑ «Recomendación UIT-T G.711: Modulación por impulsos codificados (MIC) de frecuencias vocales». Unión Internacional de Telecomunicaciones. Consultado el 17 de agosto de 2016.
- ↑ «Waveform Coding Techniques» (en inglés). Cisco Systems. Consultado el 17 de agosto de 2016.
- ↑ «G.711: The ITU-T 64 kbit/s log-PCM algorithm». ITU-T Software Tool Library 2009 User’s Manual (en inglés). Ginebra, Suiza: Unión Internacional de Telecomunicaciones. 30 de noviembre de 2009. p. 21. Consultado el 17 de agosto de 2016.
- ↑ a b c «A-Law and mu-Law Companding Implementations Using the TMS320C54x (Rev. A)» (en inglés). Texas Instruments. 7 de agosto de 2011. Consultado el 31 de agosto de 2016.
- ↑ «A-Law and mu-Law Companding Implementations Using the TMS320C54x (Rev. A)» (en inglés). Texas Intruments. Consultado el 29 de agosto de 2016.
- ↑ a b Tomasi, Wayne (2003). «Capítulo 15: Transmisión digital». En Guillermo Trujano Mendoza, ed. Sistemas de Comunicaciones Electronicas. Pearson Educación. ISBN 970-26-0316-1.







