Hamming(7,4)

Código Hamming(7,4)
Nombrado por	Richard Hamming
Clasificación
Tipo	Códigos de bloque
Longitud de bloque	7
Longitud de mensaje	4
Velocidad	4/7 ~ 0.571
Distancia	3
Tamaño de alfabeto	2
Notación	[7,4,3]2-code
Propiedades
	Código perfecto
	[editar datos en Wikidata]

Representación gráfica de los 4 bits de datos d₁ a d₄ y 3 bits de paridad p₁ a p₃ y qué bits de paridad se aplican a qué bits de datos

En teoría de códigos, Hamming (7,4) es el nombre de un código lineal de corrección de errores que codifica cuatro bits de datos en siete bits agregando tres bits de paridad. Es un miembro de una familia más grande de códigos de Hamming, aunque el término código de Hamming a menudo se refiere a este código específico que Richard Hamming introdujo en 1950. En aquel momento, Hamming trabajaba en los Bell Labs y estaba frustrado con la propensión a cometer errores del lector de tarjetas perforadas, razón por la que comenzó a trabajar en códigos de corrección de errores.^[1]

El código de Hamming agrega tres bits de verificación adicionales a cada cuatro bits de datos del mensaje. El algoritmo de Hamming (7,4) puede corregir cualquier error de un solo bit o detectar todos los errores de un solo bit y de dos bits. En otras palabras, la distancia de Hamming mínima entre dos palabras de código correctas cualesquiera es 3, y las palabras recibidas se pueden decodificar correctamente si están a una distancia de como máximo una de la palabra de código que fue transmitida por el remitente. Esto significa que para situaciones de un medio de transmisión donde no se producen errores de ráfaga, el código de Hamming (7,4) es efectivo (ya que el medio tendría que ser extremadamente ruidoso para que dos de los siete bits se inviertan).

En información cuántica, el Hamming (7,4) se utiliza como base para el código de Steane, un tipo de código CSS utilizado para la corrección de errores cuántica.

Objetivo

El objetivo de los códigos de Hamming es crear un conjunto de bits de paridad que se superpongan de modo que se pueda detectar y corregir un error de un solo bit en un bit de datos o en un bit de paridad. Si bien se pueden crear múltiples superposiciones, el método general se presenta en el artículo dedicado a los códigos de Hamming.

Bit #	1	2	3	4	5	6	7
Bit transmitido	$p_{1}$	$p_{2}$	$d_{1}$	$p_{3}$	$d_{2}$	$d_{3}$	$d_{4}$
$p_{1}$	Sí	No	Sí	No	Sí	No	Sí
$p_{2}$	No	Sí	Sí	No	No	Sí	Sí
$p_{3}$	No	No	No	Sí	Sí	Sí	Sí

Esta tabla describe qué bits de paridad cubren qué bits transmitidos en la palabra codificada. Por ejemplo, p₂ proporciona una paridad par para los bits 2, 3, 6 y 7. También detalla qué bit transmitido está cubierto por qué bit de paridad leyendo la columna. Por ejemplo, d₁ está cubierto por p₁ y p₂ pero no p₃ Esta tabla presenta un parecido sorprendente con la matriz de verificación de paridad (H) en la siguiente sección.

Además, si se eliminan las columnas de paridad de la tabla anterior

	$d_{1}$	$d_{2}$	$d_{3}$	$d_{4}$
$p_{1}$	Sí	Sí	No	Sí
$p_{2}$	Sí	No	Sí	Sí
$p_{3}$	No	Sí	Sí	Sí

entonces también será evidente la semejanza con las filas 1, 2 y 4 de la matriz del generador de código (G) que figura a continuación.

Por lo tanto, al elegir correctamente la cobertura de bits de paridad, todos los errores con una distancia de Hamming de 1 pueden detectarse y corregirse, razón principal para utilizar un código de Hamming.

Matrices de Hamming

Los códigos de Hamming se pueden calcular en términos álgebra lineal a través de matrices porque los códigos de Hamming son códigos lineales. A los efectos de los códigos de Hamming, se pueden definir dos matrices de Hamming: el código de la matriz generadora G y la matriz de comprobación de paridad H:

\mathbf {G^{T}} :={\begin{pmatrix}1&1&0&1\\1&0&1&1\\1&0&0&0\\0&1&1&1\\0&1&0&0\\0&0&1&0\\0&0&0&1\\\end{pmatrix}},\qquad \mathbf {H} :={\begin{pmatrix}1&0&1&0&1&0&1\\0&1&1&0&0&1&1\\0&0&0&1&1&1&1\\\end{pmatrix}}.

Como se mencionó anteriormente, las filas 1, 2 y 4 de G deberían resultar familiares, ya que asignan los bits de datos a sus bits de paridad:

p₁ cubre d₁, d₂, d₄
p₂ cubre d₁, d₃, d₄
p₃ cubre d₂, d₃, d₄

Las filas restantes (3, 5, 6, 7) asignan los datos a su posición en forma codificada y solo hay unos en esa fila, por lo que es una copia idéntica. De hecho, estas cuatro filas son linealmente independientes y forman la matriz identidad (por diseño, no por coincidencia).

También como se mencionó anteriormente, las tres filas de H deberían resultar familiares. Estas filas se utilizan para calcular el vector de síndrome en el extremo receptor y si el vector de síndrome es vector nulo (todo ceros), la palabra recibida no contiene errores; si no es cero, el valor indica qué bit se ha invertido.

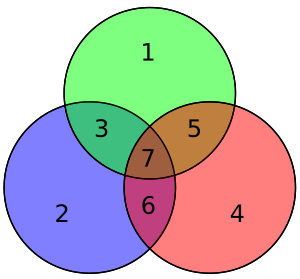
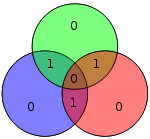
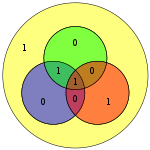
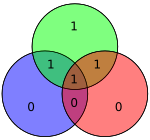
Los cuatro bits de datos — ensamblados como un vector p — se multiplican previamente por G (es decir, Gp) y se toma su módulo 2 para obtener el valor codificado que se transmite. Los 4 bits de datos originales se convierten en siete bits (de ahí el nombre "Hamming (7,4)") con tres bits de paridad añadidos para garantizar una paridad uniforme utilizando las coberturas de bits de datos anteriores. La primera tabla anterior muestra la correspondencia entre cada bit de datos y la paridad en su posición de bit final (1 a 7), pero esto también se puede presentar en un diagrama de Venn. El primer diagrama de este artículo muestra tres círculos (uno para cada bit de paridad) y encierra los bits de datos que cubre cada bit de paridad. El segundo diagrama (mostrado a la derecha) es idéntico pero, en cambio, están marcadas las posiciones de los bits.

Para el resto de esta sección, los siguientes 4 bits (mostrados como un vector columna) se utilizarán como un ejemplo de ejecución:

\mathbf {p} ={\begin{pmatrix}d_{1}\\d_{2}\\d_{3}\\d_{4}\\\end{pmatrix}}={\begin{pmatrix}1\\0\\1\\1\end{pmatrix}}

Codificación de canal

Supóngase que se desea transmitir los datos (1011) a través de un canal de comunicación con ruido. Específicamente, un canal binario simétrico implica que la corrupción generadora de errores no favorece ni a cero ni a uno (es decir, es simétrica al causar errores). Además, se supone que todos los vectores fuente son equiprobables. Tomando el producto de G y p, con entradas módulo 2, para determinar la palabra de código transmitida x:

\mathbf {x} =\mathbf {G} \mathbf {p} ={\begin{pmatrix}1&1&0&1\\1&0&1&1\\1&0&0&0\\0&1&1&1\\0&1&0&0\\0&0&1&0\\0&0&0&1\\\end{pmatrix}}{\begin{pmatrix}1\\0\\1\\1\end{pmatrix}}={\begin{pmatrix}2\\3\\1\\2\\0\\1\\1\end{pmatrix}}={\begin{pmatrix}0\\1\\1\\0\\0\\1\\1\end{pmatrix}}

Esto significa que se transmitiría 0110011 en lugar de transmitirse 1011.

Los programadores preocupados por la multiplicación deben observar que cada fila del resultado es el bit menos significativo del conteo de población de los bits establecidos que resultan de la fila y de la columna sumados en lugar de multiplicados.

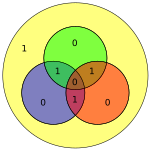
En el diagrama adyacente, los siete bits de la palabra codificada se insertan en sus respectivas ubicaciones; de la inspección es claro que las paridades de los círculos rojo, verde, y azul son pares:

el círculo rojo tiene dos unos
el círculo verde tiene dos unos
el círculo azul tiene cuatro unos

Lo que se mostrará en breve es que si, durante la transmisión, se invierte un bit, la paridad de dos o de los tres círculos será incorrecta y el bit con error se puede determinar (incluso si es uno de los bits de paridad) sabiendo que las paridades de los tres círculos deben ser pares.

Verificación de paridad

Si no se produce ningún error durante la transmisión, entonces la palabra de código recibida r es idéntica a la palabra de código transmitida x:

\mathbf {r} =\mathbf {x}

El receptor multiplica H y r para obtener el vector de síndrome z, que indica si se ha producido un error y, de ser así, en qué bit de la palabra de código. Realizando esta multiplicación (nuevamente, con entradas módulo 2):

\mathbf {z} =\mathbf {H} \mathbf {r} ={\begin{pmatrix}1&0&1&0&1&0&1\\0&1&1&0&0&1&1\\0&0&0&1&1&1&1\\\end{pmatrix}}{\begin{pmatrix}0\\1\\1\\0\\0\\1\\1\end{pmatrix}}={\begin{pmatrix}2\\4\\2\end{pmatrix}}={\begin{pmatrix}0\\0\\0\end{pmatrix}}

Dado que el síndrome z es el vector nulo, el receptor puede concluir que no se ha producido ningún error. Esta conclusión se basa en la observación de que cuando el vector de datos se multiplica por G, se produce un cambio de base en un subespacio vectorial que es el núcleo de H. Mientras no ocurra nada durante la transmisión, r permanecerá en el núcleo de H y la multiplicación producirá el vector nulo.

Corrección de errores

De lo contrario, supóngase que se ha producido un único error de bit. Matemáticamente, se puede escribir

\mathbf {r} =\mathbf {x} +\mathbf {e} _{i}

módulo 2, donde e_i es el $i_{\text{ésimo}}$ vector unitario, es decir, un vector cero con un 1 en la $i^{\text{ésima}}$ posición contando desde 1.

\mathbf {e} _{2}={\begin{pmatrix}0\\1\\0\\0\\0\\0\\0\end{pmatrix}}

Por lo tanto, la expresión anterior significa un error de un solo bit en el lugar $i^{\text{ésimo}}$ .

Ahora, si se multiplica este vector por H:

\mathbf {Hr} =\mathbf {H} \left(\mathbf {x} +\mathbf {e} _{i}\right)=\mathbf {Hx} +\mathbf {He} _{i}

Dado que x son los datos transmitidos, no hay error y, como resultado, el producto de H y x es cero. Por lo tanto

\mathbf {Hx} +\mathbf {He} _{i}=\mathbf {0} +\mathbf {He} _{i}=\mathbf {He} _{i}

Ahora, el producto de H por el vector base estándar $i^{\text{ésimo}}$ selecciona esa columna de H, y se sabe que el error se produce en el lugar donde se altera esta columna de H.

Por ejemplo, supóngase que se ha introducido un error de bit en el bit # 5

\mathbf {r} =\mathbf {x} +\mathbf {e} _{5}={\begin{pmatrix}0\\1\\1\\0\\0\\1\\1\end{pmatrix}}+{\begin{pmatrix}0\\0\\0\\0\\1\\0\\0\end{pmatrix}}={\begin{pmatrix}0\\1\\1\\0\\1\\1\\1\end{pmatrix}}

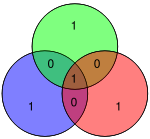
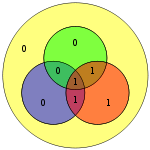
El diagrama de la derecha muestra el error de bit (mostrado en texto azul) y la paridad incorrecta creada (mostrada en texto rojo) en los círculos rojo y verde. El error de bit se puede detectar calculando la paridad de los círculos rojo, verde y azul. Si se detecta una paridad incorrecta, el bit de datos que se superpone solo a los círculos de paridad incorrecta es el bit con el error. En el ejemplo anterior, los círculos rojo y verde tienen mala paridad, por lo que el bit correspondiente a la intersección de rojo y verde, pero no azul, indica el bit con el error.

Ahora,

\mathbf {z} =\mathbf {Hr} ={\begin{pmatrix}1&0&1&0&1&0&1\\0&1&1&0&0&1&1\\0&0&0&1&1&1&1\\\end{pmatrix}}{\begin{pmatrix}0\\1\\1\\0\\1\\1\\1\end{pmatrix}}={\begin{pmatrix}3\\4\\3\end{pmatrix}}={\begin{pmatrix}1\\0\\1\end{pmatrix}}

que corresponde a la quinta columna de H. Además, el algoritmo general utilizado (véase Código Hamming) se diseño intencionadamente, de modo que el síndrome de 101 corresponde al valor binario de 5, lo que indica que el quinto bit estaba dañado. Por lo tanto, se ha detectado un error en el bit 5 y se puede corregir (simplemente invirtiendo o negando su valor):

\mathbf {r} _{\text{corrected}}={\begin{pmatrix}0\\1\\1\\0\\{\overline {1}}\\1\\1\end{pmatrix}}={\begin{pmatrix}0\\1\\1\\0\\0\\1\\1\end{pmatrix}}

El valor recibido, una vez corregido, coincide con el valor x anteriormente considerado.

Decodificación

Una vez que se ha determinado que el vector recibido está libre de errores, o si se produjo un error se ha corregido (suponiendo que solo son posibles errores de un bit o cero), los datos recibidos deben decodificarse nuevamente en los cuatro bits originales.

Primero, se define una matriz R:

\mathbf {R} ={\begin{pmatrix}0&0&1&0&0&0&0\\0&0&0&0&1&0&0\\0&0&0&0&0&1&0\\0&0&0&0&0&0&1\\\end{pmatrix}}

Entonces el valor recibido, p_r, es igual a Rr. Usando el ejemplo de ejecución de arriba

\mathbf {p_{r}} ={\begin{pmatrix}0&0&1&0&0&0&0\\0&0&0&0&1&0&0\\0&0&0&0&0&1&0\\0&0&0&0&0&0&1\\\end{pmatrix}}{\begin{pmatrix}0\\1\\1\\0\\0\\1\\1\end{pmatrix}}={\begin{pmatrix}1\\0\\1\\1\end{pmatrix}}

Errores de bits múltiples

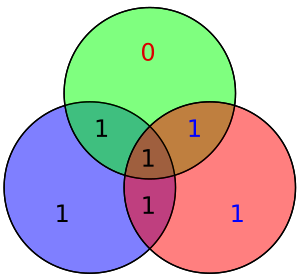
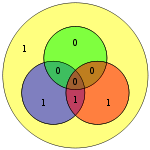
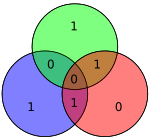
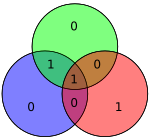
No es difícil demostrar que únicamente los errores de un solo bit pueden corregirse utilizando este procedimiento. Alternativamente, los códigos de Hamming se pueden usar para detectar errores de bit simple y doble, simplemente notando que el producto de H es distinto de cero siempre que hayan ocurrido errores. En el diagrama adyacente, los bits 4 y 5 se invirtieron. Esto produce solo un círculo (verde) con una paridad no válida, pero los errores no se pueden recuperar.

Sin embargo, los códigos de Hamming(7,4) y Hamming similares no pueden distinguir entre errores de un solo bit y errores de dos bits. Es decir, los errores de dos bits tienen el mismo aspecto que los errores de un bit. Si se realiza la corrección de errores en un error de dos bits, el resultado será incorrecto.

De manera similar, los códigos de Hamming no pueden detectar o recuperar un error arbitrario de tres bits. Para verlo, considérese el diagrama: si el bit en el círculo verde (de color rojo) fuera 1, la verificación de paridad devolvería el vector nulo, lo que indica que no hay error en la palabra de código.

Todas las palabras del código

Dado que la fuente tiene solo 4 bits, solo hay 16 palabras transmitidas posibles. Se incluye el valor de ocho bits si se utiliza un bit de paridad adicional (véase código Hamming(7,4) con un bit de paridad adicional). Aquí, los bits de datos se muestran en azul; los bits de paridad se muestran en rojo; y el bit de paridad adicional se muestra en amarillo.

Dato $({\color {blue}d_{1}},{\color {blue}d_{2}},{\color {blue}d_{3}},{\color {blue}d_{4}})$	Hamming(7,4)		Hamming(7,4) con bit de paridad extra (Hamming(8,4))
	Transmitido $({\color {red}p_{1}},{\color {red}p_{2}},{\color {blue}d_{1}},{\color {red}p_{3}},{\color {blue}d_{2}},{\color {blue}d_{3}},{\color {blue}d_{4}})$	Diagrama	Transmitido $({\color {red}p_{1}},{\color {red}p_{2}},{\color {blue}d_{1}},{\color {red}p_{3}},{\color {blue}d_{2}},{\color {blue}d_{3}},{\color {blue}d_{4}},{\color {green}p_{4}})$	Diagrama
0000	0000000		00000000
1000	1110000		11100001
0100	1001100		10011001
1100	0111100		01111000
0010	0101010		01010101
1010	1011010		10110100
0110	1100110		11001100
1110	0010110		00101101
0001	1101001		11010010
1001	0011001		00110011
0101	0100101		01001011
1101	1010101		10101010
0011	1000011		10000111
1011	0110011		01100110
0111	0001111		00011110
1111	1111111		11111111

Retícula E₇

El código Hamming (7,4) está estrechamente relacionado con la retícula E₇ y, de hecho, se puede usar para construirla, o más precisamente, su doble retícula E₇^∗ (una construcción similar para E₇ usa el código dual [7,3,4]₂). En particular, tomando el conjunto de todos los vectores x en Z⁷ con x congruente (módulo 2) a una palabra en clave de Hamming (7,4), y reescalado por 1/√2, da la retícula E₇^∗

E_{7}^{*}={\tfrac {1}{\sqrt {2}}}\left\{x\in \mathbb {Z} ^{7}:x\,{\bmod {\,}}2\in [7,4,3]_{2}\right\}.

Este es un ejemplo particular de una relación más general entre retículas y códigos. Por ejemplo, el código extendido (8,4)-Hamming, que surge de la adición de un bit de paridad, también está relacionado con la retícula E₈.^[2]

Referencias

↑ «History of Hamming Codes». Archivado desde el original el 25 de octubre de 2007. Consultado el 3 de abril de 2008.
↑ Conway, John H.; Sloane, Neil J. A. (1998). Sphere Packings, Lattices and Groups (3rd edición). New York: Springer-Verlag. ISBN 0-387-98585-9. (requiere registro).

Enlaces externos

Un problema de programación sobre el Código Hamming (7,4)

Datos: Q2322550

[1] «History of Hamming Codes». Archivado desde el original el 25 de octubre de 2007. Consultado el 3 de abril de 2008.

[Conway-2] Conway, John H.; Sloane, Neil J. A. (1998). Sphere Packings, Lattices and Groups (3rd edición). New York: Springer-Verlag. ISBN 0-387-98585-9. (requiere registro).

[1]

[2]