Gran antiprisma

Gran antiprisma
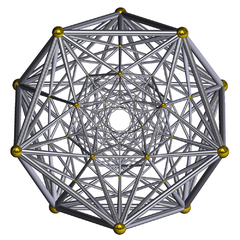(Esquema alámbrico del diagrama de Schlegel)
Tipo	4 politopo uniforme
Índice uniforme	47
Células	100+200 (3.3.3) 20 (3.3.3.5)
Caras	20 {5} 700 {3}
Aristas	500
Vértices	100
Figura de vértice	Esfenocorona
Grupo de simetría	Grupo Coxeter disminuido iónico [[10,2+,10]] de orden 400
Símbolo de Schläfli	s{5}.s{5} (extendido)
Propiedades	convexo
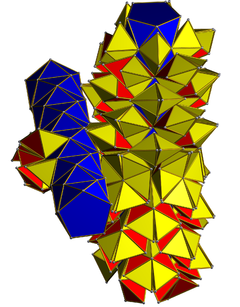Una red mostrando dos anillos disjuntos de 10 antiprismas. 200 tetraedros (amarillo) se encuentran en contacto con las caras de los antiprismas y 100 tetraedros (rojos) en contacto con otros tetraedros.

En el ámbito de la geometría, se denomina gran antiprisma o antiprismoide doble pentagonal a un 4-politopo uniforme (politopo uniforme 4 dimensional) delimitado por 320 celdas: 20 antiprismas pentagonales, y 300 tetraedros. Es un 4-politopo uniforme no-Wythoffiano, anómalo descubierto en 1965 por Conway y Guy.​​ Desde un punto de vista topológico, su simetría más elevada, los antiprismas pentagonales tienen simetría  D_5d y existen dos tipos de tetraedros, uno con simetría S₄ y uno con simetría  C_s.

Nombres alternativos

• Antiprismoide doble pentagonal Norman W. Johnson
• Gap (Jonathan Bowers: en referencia a gran antiprisma)​

Estructura

20 antiprismas pentagonales apilados se organizan en dos anillos disjuntos cada uno de ellos con 10 antiprismas. Los antiprismas en cada anillo se encuentran vinculados entre sí a través de las caras pentagonales. Los dos anillos son mutuamente perpendiculares, en una estructura similar a un duoprisma.

Los 300 tetraedros se unen en dos anillos entre sí, y se encuentran dispuestos en un esquema bidimensional topológicamente equivalente a los bi toroides y el borde del duocilindro. Estos a su vez pueden ser divididos en tres conjuntos. 100 se conectan a través de sus caras a un anillo, 100 se conectan a través de sus caras al otro anillo, y 100 se encuentran centrados en el centro exacto del duocilindro y se conectan por sus aristas a ambos anillos. Este último conjunto forma un toroide plano y puede ser "desarrollado" en un esquema plano cuadrado de 10×10 de tetraedros que se encuentran solo en sus bordes y vértices. Ver la figura adjunta.

100 tetraedros en un arreglo de 10×10 forman la periferia del toroide de Clifford en el hexacosicoron y el gran antiprisma.

Además los 300 tetraedros pueden ser partidos en 10 hélices de Boerdijk–Coxeter disjuntas con 30 celdas cada una que se cierran entre sí. Los dos tubos antiprismas pentagonales, más las 10 hélices BC, forman una fibración de Hopf discreta irregular del gran antiprisma que mapea en un modo Hopf con las caras de un antiprisma pentagonal. Los dos tubos se mapean con las dos caras pentagonales y las 10 BC hélices BS se mapean con las 10 caras triangulares.

La estructura del gran antiprisma es análoga a la estructura de los antiprismas de tres dimensiones. Sin embargo, el gran antiprisma es el único análogo uniforme convexo al antiprisma en 4 dimensiones (si bien el 16-cell puede ser considerado un análogo regular del antiprisma diagonal). El único antiprisma análogo uniforme 4-dimensional noconvexo usa antiprismas cruzados pentagrámicos en vez de antiprismas pentagonales, y es denominado el antiprismoide doble pentagrámico.

Figura de vértice

La figura de vértice del gran antiprisma es una esfenocorona o icosaedro regular disectado: un icosaedro regular al que se le han quitado dos vértices adyacentes. En su lugar 8 triángulos son reemplazados por un par de trapezoides, cuyo largo de sus laterales es φ, 1, 1, 1 (donde φ es la relación áurea), adosados a lo largo de sus bordes de largo φ, para producir un tetradecaedro cuyas caras son los 2 trapezoides y los 12 triángulos equiláteros restantes.

12 (3.3.3)

2 (3.3.3.5)

Icosaedro regular disectado

Construcción

El hexacosicoron regular puede ser descompuesto con la geometría del gran antiprisma, donde cada uno de los 20 antiprismas pentagonales azules es dividido en 15 tetraedros regulares.

El gran antiprisma puede ser construido reduciendo un hexacosicoron: substrayendo 20 pirámides cuyas bases son antiprismas pentagonales tridimensionales. En forma opuesta, los dos anillos de los antiprismas pentagonales en el gran antiprisma pueden ser triangulados mediante 10 tetraedros unidos por las caras triangulares de cada antiprisma, y un círculo de 5 tetraedros entre cada par de antiprismas, uniendo los 10 tetraedros de cada uno, resultando así 150 tetraedros por anillo. Estos junto con los 300 tetraedros que se adosan a los dos anillos producen los 600 tetraedros del hexacosicoron.

Esta reducción puede ser realizada quitando dos anillos de 10 vértices del hexacosicoron, cada uno ubicado en planos mutuamente ortogonales. Cada anillo de vértices eliminados genera una torre de antiprismas pentagonales en la envolvente convexa. Esta relación es análoga a como se puede construir un antiprisma pentagonal a partir de un icosaedro quitando dos vértices opuestos, o sea quitando 5 triángulos de los 'polos' opuestos del icosaedro, dejando los 10 triángulos ecuatoriales y dos pentágonos en la parte superior e inferior.

(El 24-celda snub (ver Icositetracoron) también puede ser construido mediante otra reducción del hexacosicoron, quitando 24 pirámides icosaedras. De manera equivalente, ello se puede entender como la envolvente convexa de los vértices remanente luego que 24 vértices, correspondientes a aquellos de una 24-celda inscripta, son quitados del hexacosicoron.)

Alternativamente, también puede ser construido a partir del ditetragoltriado decagonal (la envolvente convexa de dos 10-10 duoprismas nouniformes perpendiculares donde la relación de los dos decágonos es la relación áurea) mediante un proceso de alternancia. Los prismas decagonales alternados en antiprismas pentagonales, los trapezoprismas rectangulares se alternan en tetraedros con dos tetraedros nuevos regulares (representando una bi pirámide triangular no-corealmica) creados en los vértices eliminados. Esta es la única solución uniforme de antiprismoides dobles p-gonales a lo largo de su conjugado, el antiprismoide doble pentagrámico del ditetragoltriado decagramático.

Proyecciones ortogonales

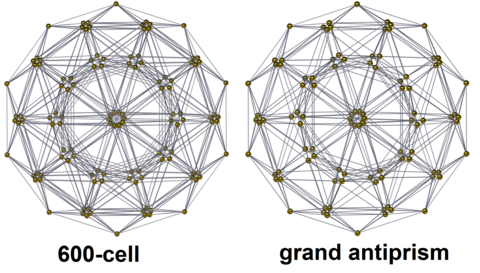
Hexacosicoron	Gran antiprisma
H4 Plano Coxeter
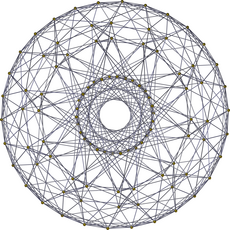
20-gonal
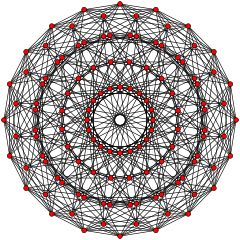
H3 Plano Coxeter (levemente desplazado)

Proyecciones

Estas son dos proyecciones en perspectiva, proyectando el politopo en una hiperesfera, y aplicando una proyección estereográfica en un 3-espacio.

Esquema de alambres, visto a lo largo de una de las columnas antiprismas pentagonales.	con caras triangulares transparentes
Proyección ortográfica Centrada en el hiperplano de un antiprisma en uno de los dos anillos.	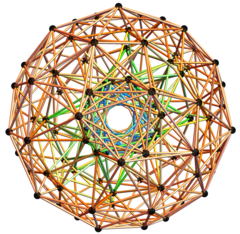proyección ortográfica 3D de 100 de los 120 600-cell vértices y 500 bordes {488 de 1/2 (3-Sqrt[5]) y 12 de 2/(3+Sqrt[5])}.

Véase también

• Hexacosicoron
• 4-politopo uniforme
• Duoprisma
• Duocilindro

Bibliografía

• Kaleidoscopes: Selected Writings of H.S.M. Coxeter, edited by F. Arthur Sherk, Peter McMullen, Anthony C. Thompson, Asia Ivic Weiss, Wiley-Interscience Publication, 1995, ISBN 978-0-471-01003-6
  • (Paper 23) H.S.M. Coxeter, Regular and Semi-Regular Polytopes II, [Math. Zeit. 188 (1985) 559-591] 2.8 The Grand Antiprism
• Klitzing, Richard. «4D uniform polytopes (polychora) gap». 

• John H. Conway, Heidi Burgiel, Chaim Goodman-Strass, The Symmetries of Things 2008, ISBN 978-1-56881-220-5 (Chapter 26) The Grand Antiprism
• Grand Antiprism and Quaternions [1] Mehmet Koca, Mudhahir Al-Ajmi, Nazife Ozdes Koca (2009); Mehmet Koca et al. 2009 J. Phys. A: Math. Theor. 42 495201

Enlaces externos

• En el ombligo del Gran Antiprisma Archivado el 7 de febrero de 2006 en Wayback Machine. (Sección central, describiendo la analogía con los antiprisma icosaedro y pentagonal)

• Datos: Q3890147