Geometría computacional

La geometría computacional es una rama de las ciencias de la computación dedicada al estudio de algoritmos que pueden ser expresados en términos de la geometría. Algunos de los problemas puramente geométricos surgen del propio estudio de dichos algoritmos, y este tipo de problemas también se considera parte de la geometría computacional.[1] También se considera una rama gráfica del ordenador.
Introducción
[editar]Una parte significativa del crecimiento que la Matemática Discreta, como un todo, ha experimentado en los últimos años, ha consistido en un desarrollo sustancial de la Geometría Discreta. Esto ha sido impulsado, en parte, por el desarrollo de ordenadores cada vez más potentes, y por la reciente explosión de actividad en el campo relativamente joven de la Geometría Computacional.
¿Y qué es la Geometría Computacional? En pocas palabras, es el arte de resolver problemas conceptualmente sencillos usando los menos recursos posibles y empleando el mínimo tiempo posible. La Geometría Computacional surgió a finales de los 70s del área de diseño y análisis de algoritmos. La mayoría de los estudios algorítmicos que abordaban estos problemas han ido apareciendo a lo largo de los últimos 150 años, aunque sobre todo en los últimos treinta. De todas formas, sólo muy recientemente han sido realizados estudios sistemáticos de algoritmos geométricos y cada día más investigadores se sienten atraídos por la disciplina que fue bautizada en 1975 por Shamos.
Hasta hace poco, Geometría Computacional se refería al diseño y análisis de algoritmos geométricos, pero en los últimos años ha ampliado su campo, y ahora también incluye el estudio de problemas geométricos desde un punto de vista computacional, incluyendo también convexidad computacional, topología computacional y complejidad combinatorial de disposiciones de poliedros.
En los últimos años ha aumentado el número de áreas en las que se aplican los resultados de esta disciplina. Entre las mismas se incluyen la ingeniería, cristalografía, diseño asistido por computador, sistemas de posicionamiento global, robótica, sistemas de detección de errores, modelado geométrico, gráficos por ordenador, optimización combinatorial, visión por ordenador, reconocimiento de patrones y modelado sólido.
Descripción
[editar]Es una disciplina constructiva, de carácter abstracto, que utiliza técnicas de la geometría clásica, la topología, la teoría de grafos, la teoría de conjuntos y el álgebra lineal. La geometría computacional es independiente de la tecnología de las máquinas de computación, si bien pone atención en proporcionar soluciones que se comporten de forma computacionalmente robusta.
La complejidad computacional es fundamental para la geometría computacional, con un enorme significado práctico si los algoritmos se usan en grandes conjuntos de datos que contienen decenas o cientos de millones de puntos. Para tales conjuntos, la diferencia entre O(n^2) y O(n logn) puede ser la diferencia entre días o segundos de computación.
El principal impulso para el desarrollo de la geometría computacional se lo dio el avance de la computación gráfica y el diseño asistido por ordenador (CAD/CAM), que hacen uso intensivo de las técnicas de esta disciplina. Otras aplicaciones importantes de la geometría computacional incluyen la robótica (planificación de movimientos y problemas de visualización), los sistemas de información geográfica (SIG) (localización y búsqueda geométrica, planificación de rutas), diseño de circuitos integrados (diseño geométrico y verifición de CI), ingeniería asistida por computadora (CAE) (programación de máquinas controladas numéricamente).
Las principales ramas de la geometría computacional son:
- Geometría computacional combinatoria, también llamada geometría algorítmica, que trata de objetos geométricos como entidades discretas. Un libro sobre el tema por Preparata y Shamos fecha la primera utilización del término "geometría computacional" en este sentido en 1975.[2][1]
- Geometría computacional numérica, que trata principalmente con la representación de objetos del mundo real en la forma adecuada para ser almacenada en un ordenador. Esta rama puede ser vista como un desarrollo de la geometría descriptiva y es a menudo considerada como una rama de los gráficos por ordenador o CAD. El término "geometría computacional", en este sentido ha estado en uso desde 1971.[3]
Complejidad algorítmica
[editar]Frecuentemente se tiene que un mismo problema puede resolverse mediante distintos algoritmos y es preciso establecer criterios que nos permita decidir cuál es mejor. En general se atiende a razones de economía en cuanto al número de operaciones que necesita el algoritmo para resolver el problema.
La complejidad de un algoritmo no es sino una medida del coste que supone su ejecución tanto en tiempo (o número de operaciones "elementales" que ha de realizar) como en espacio (o unidades de memoria requeridas para almacenar y manipular los datos a lo largo de la ejecución) y vendrá dada en función del número de datos de entrada.
El estudio de la complejidad de un algoritmo puede llevarse a cabo principalmente bajo dos puntos de vista:
* Complejidad en el peor de los casos.
* Complejidad en media (o esperada).
La primera consiste en medir la complejidad del algoritmo atendiendo a su ejecución cuando trata los datos del problema en el caso más desfavorable, entendiéndose por desfavorable el más costoso.
La segunda consiste en medir la complejidad haciendo un promedio entre todos los casos (favorables y no favorables) atendiendo a la probabilidad de que aparezcan como entrada. Para ello se supone que los datos de entrada vienen dados conforme a cierta distribución de probabilidad y se estudia cuál es el tiempo esperado de ejecución.
Si n es el tamaño del conjunto de datos de entrada de un determinado algoritmo, sus complejidades en tiempo y en espacio son funciones positivas de n y, en cuanto a su análisis, se está especialmente interesado en su comportamiento asintótico, es decir, en saber cómo se comportan para valores grandes de n.
La notación que utilizaremos en el estudio asintótico de estas funciones es la estándar propuesta por Knuth:
Si f(n) y g(n) dos funciones positivas se dirá que
1. "f es o grande de g" y se notará f(n) = O(g(n)) si existen una constante C > O y un número natural n0 > O tales que
f(n) menor Cg(n) para todo n > n0
2. "f es omega de g" y se notará f(n) Q(g(n)) si g(n) = O(f(n))
3. "f es theta de g" y se notará f(n) = O(g(n)) si f(n) = O(g(n)) y f(n) = Q(g(n)).
Geometría computacional combinatoria
[editar]
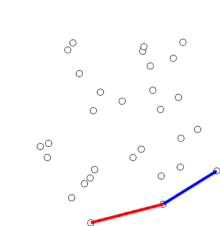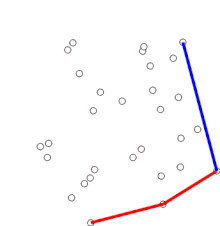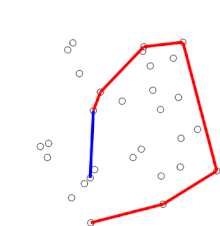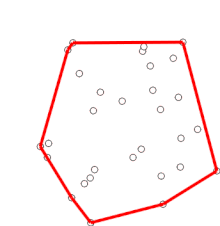

El objetivo principal de la geometría computacional combinatoria es el desarrollo de algoritmos y estructuras de datos eficientes para resolver problemas basado en términos de objetos geométricos: puntos, segmentos, polígonos, poliedros, etc...
Algunos de estos problemas parecen tan simples que no fueron considerados como tal hasta la llegada de los ordenadores. Por ejemplo, la determinación del cierre convexo de un conjunto de puntos puede ser realizada de forma intuitiva sobre un papel utilizando una regla, pero no es tan evidente dar las instrucciones a un ordenador para que lo resuelva. Otro problema, el de encontrar el par de puntos más cercanos puede ser implementado de forma sencilla mediante una búsqueda por fuerza bruta, calculando la distancia entre las n(n-1)/2 combinaciones posibles de pares de puntos y eligiendo la menor, pero esta solución no es aplicable para conjuntos con un elevado número de puntos. [4] [5]
Algunos problemas clásicos
[editar]A continuación se enumeran algunos problemas clásicos que han sido estudiados en el campo de la Geometría computacional combinatoria:[6][7][8][9]
- Cierre convexo: Dado un conjunto de puntos, encontrar el polígono convexo de menor área que los contenga.
- Triangulación de un polígono: Descomponer un polígono en una serie de triángulos que lo recubran.
- Problema del par de puntos más cercanos: Dado un conjunto de puntos, encontrar el par de puntos más próximos entre sí.
- Diámetro de un conjunto de puntos: Dado un conjunto de puntos, encontrar el par de puntos más alejados entre sí.
- Problema del mayor círculo vacío: Dado un conjunto de puntos, encontrar el mayor círculo con centro dentro del cierre convexo y que no contenga ningún punto.
- Intersección de segmentos de recta: Dado un conjunto de segmentos en el plano, encontrar todos los puntos de intersección en segmentos.
- Operaciones booleanas sobre polígonos: Calcular de forma eficiente uniones/intersecciones entre polígonos.
- Problema de la galería de arte: Determinar el mínimo número de puntos de un polígono que son suficientes para ver a todos los restantes.
- Búsqueda de rango: Dado un conjunto de puntos, encontrar aquellos en el interior de una figura geométrica dada.
Problemas dinámicos
[editar]Otra gran clase es la de los problemas dinámicos, en la cual el objetivo es encontrar un algoritmo eficiente para encontrar la solución repetidamente tras cada modificación incremental de los datos de entrada (adición o supresión de los elementos geométricos de entrada). Los algoritmos para los problemas de este tipo típicamente supone estructuras dinámicas de datos. Cualquiera de los problemas de geometría computacional puede ser convertido en uno dinámico, con el coste de incrementar el tiempo del proceso. Por ejemplo, el problema de la búsqueda de rango provisto de adición y/o supresión de los puntos. El problema de la Envolvente convexa dinámica es mantener un seguimiento de la envolvente convexa; por ejemplo, para los conjuntos de datos que cambian dinámicamente, o mientras que los puntos de entrada son insertados o suprimidos. La complejidad computacional para esta clase de problemas se estima mediante:
- El tiempo y espacio requeridos para construir la estructura de datos que se va a buscar.
- El tiempo y espacio para modificar la estructura de datos buscada después de un cambio incremental en el espacio de búsqueda.
- El tiempo (y a veces un extra de espacio) para responder la consulta.
Sistemas de Geometría Dinámica (SGD/DGS) el término sistema aludiendo a un conjunto integrado de componentes como principal elemento un núcleo o kernel de geometría dinámica computacional con interfaz gráfica de usuario (GUI) y en algunos casos incluye scripts para automatizar procedimientos como lo realiza la aplicación GeoGebra
Variantes
[editar]Algunos problemas pueden ser tratados bajo el punto de vista estático y dinámico dependiendo del contexto. Por ejemplo, considerando el siguiente problema:
- Punto en un polígono: Decide si un punto está dentro o fuera de un polígono dado.
Muchas de las puestas en práctica de este problema dan resultados con un único intento, esto es, perteneciendo a la primera clase. Por ejemplo, en muchas aplicaciones de la computación gráfica, un problema común es encontrar en qué área de la pantalla se hace clic con el cursor. Sin embargo, en algunas aplicaciones el polígono en cuestión es invariante, mientras que el punto representa una consulta. Por ejemplo, el polígono de entrada puede representar la frontera de un país y el punto es la posición de un avión, y el problema es determinar si el avión ha violado la frontera. Finalmente, el ejemplo anteriormente mencionado de la computación gráfica, en aplicaciones CAD los datos de entrada que cambian son usualmente almacenados en estructuras de datos dinámicas, lo cual puede ser explotado para agilizar las consultas de punto en un polígono. En algunos contextos de problemas de consultas hay expectativas razonables en la secuencia de las consultas, la cual puede ser aprovechada ya sea por estructuras de datos eficientes o por estimaciones de la complejidad computacional más ajustadas. Por ejemplo, en algunos casos es importante saber el peor caso para el tiempo total de la secuencia de N consultas antes que el de una única consulta.
Aplicaciones de la geometría computacional
[editar]Uno de los aspectos más interesantes de la Geometría Computacional es la gran aplicabilidad de sus resultados.
El significado del término computación se ha expandido notoriamente desde la introducción de los ordenadores, hará ahora unos cincuenta años.
Atendiendo a los objetos que procesan, destacan tres tipos de aplicaciones de los ordenadores. La primera generación va a ser la de los cálculos numéricos, aplicados sobre todo a problemas científicos y técnicos. La segunda, propiciada por necesidades más comerciales y administrativas, incorporaba largas listas de datos (por ejemplo alfabéticos), con vistas a cómo leer, almacenar, modificar, seleccionar, e imprimir esos datos.
Todo esto naturalmente pervive, y con fuerza, pero vivimos una tercera generación de aplicaciones dominada por el procesamiento de información geométrica y gráfica, presente en áreas tan diversas como son la medicina, la cartografía, el control de robots o el diseño artístico. La Geometría Computacional ha emergido, ciertamente, por la necesidad de dar respuesta a esta nueva y creciente demanda.
Se podría decir que las aplicaciones van a preceder la disciplina, y ahora que ésta tiene ya un núcleo teórico sólidamente constituido, como sus vertientes prácticas corresponden a tecnología de máxima vanguardia, la demanda de resultados continúa con la misma fuerza y exigencia que al principio. Por eso diremos que, en Geometría Computacional, las aplicaciones tienen un protagonismo esencial.
Dentro de los campos de aplicación más directamente relacionados con la disciplina se destacan:
La Informática Gráfica
El Diseño y Fabricación Asistida por Ordenador (CAD/CAM)
La Caracterización y Reconocimiento Automático de Formas (Pattern Recognition)
El Diseño VLSI
La Visión Artificial
La Cartografía
La Robótica
A continuación se muestran algunos problemas particulares que se plantean en algunas de estas áreas, y en las que se han realizado contribuciones (en algunos casos, muy importantes) por parte de la Geometría.
Gráficos por ordenador
[editar]Lo que se entiende hoy por Gráficos por Ordenador (o Informática Gráfica), pese a ser una rama de Informática que también se ocupa de los fenómenos geométricos desde el punto de vista del cálculo, es un área bien distinta de la Geometría Computacional.
Mientras que ésta se ocupa de proporcionar los fundamentos teóricos involucrando el estudio de algoritmos y de estructuras de datos para hacer cálculos geométricos, la Informática Gráfica se ocupa del desarrollo práctico del software, hardware y algoritmos necesarios para crear gráficos en la pantalla del ordenador.
Sin embargo, ambas tienen algunas técnicas similares (otras muy distintas), y sin duda alguna, se influencian mutuamente. Desde el ámbito de los informática gráfica se dan a conocer problemas prácticos a la comunidad de estudiosos de la Geometría Computacional, y la Geometría Computacional aporta algoritmos rápidos que los resuelven. Se espera que la Geometría Computacional haga grandes mejoras a los algoritmos estándar usados en gráficos por ordenador.
La Geometría Computacional también proporciona nuevas maneras de pensar los problemas a los programadores de gráficos.
Una cuestión muy importante en informática gráfica es la representación realista de escenas complejas. Uno de los requisitos es la eliminación de líneas y superficies ocultas a partir de un modelo tridimensional. Las primeras soluciones razonablemente satisfactorias van a iniciar áreas importantes de investigación dentro de la geometría computacional, concretamente los problemas de intersección. Los resultados de estas investigaciones han dado nuevas aplicaciones en informática gráfica. De modo que hay una interacción continua en este problema como en otros muchos otros.
Otros problemas fundamentales que aparecen en Gráficos son: el trazado de rayos, la aproximación de contornos mediante poligonales y la triangulación de polígonos. En todos ellos la Geometría Computacional ha realizado recientemente contribuciones significativas.
En una habitación poligonal (galería de arte) en el plano se colocan cuatro cámaras de manera que se pueda vigilar con ellas toda la sala. Si se está interesado en averiguar cuál es la región que es visible por una sola cámara esto es equivalente a eliminar las porciones del polígono que quedan ocultas. Uno de los algoritmos estándar usado para resolver este problema de líneas ocultas en el plano es el debido a Freeman y Loutrel hace más de diez años antes de lo que se atribuye como el nacimiento de la Geometría Computacional. Dicho algoritmo corre en tiempo 0(n2) donde n es el número de lados del polígono.
Utilizando técnicas desarrolladas para el diseño de algoritmos en Geometría Computacional, ElGindy y Avis consiguieron un algoritmo para este problema que corre en tiempo (óptimo) 0(n), cuando n es grande esto supone una mejora sustancial en la velocidad de ejecución.
Fabricación industrial
[editar]A continuación, algunos ejemplos en este campo.
Modelado por inyección
[editar]Una de las técnicas utilizadas en la fabricación industrial de objetos consiste en utilizar moldes en los que se inyectan ciertos materiales líquidos que al solidificar dan lugar al objeto requerido con la forma imprimida por el molde.
Durante la inyección del líquido, el molde es colocado en una posición favorable de manera que no aparezcan defectos en la superficie tales como burbujas de aire y se garantice un llenado completo. Dos de los problemas que surgen en este contexto son: dado un objeto tridimensional como molde , establecer si existe una orientación que permite el llenado del molde usando sólo un punto de inyección y determinar una orientación que permita el llenado más completo.
Habitualmente en la práctica se sigue un proceso de prueba y error utilizando ciertas técnicas intuitivas.
Robótica
[editar]Una de las principales aplicaciones de Geometría Computacional tiene que ver con problemas de robótica. Dos ejemplos de ellos: la planificación de movimientos y el ensamblaje automático.
En el primero, el problema típico involucra un robot, generalmente modelizado como un punto, un disco, o un polígono en dos dimensiones, o bien como un poliedro en tres dimensiones que ha de moverse en el espacio entre una colección de obstáculos. Una de las preguntas usuales es ¿puede moverse el robot desde un punto A a otro B sin colisionar con los obstáculos?
Si es así, se deberá encontrar la trayectoria más corta. Localización de una trayectoria libre de colisiones.
El ensamblaje automático es un caso especial de problema de planificación de movimientos en el que consideramos una colección de objetos y la pregunta es si puede ser separada en partes o unir en una configuración determinada, y si es así, qué tipo de movimientos (giros, traslaciones, etc.) garantizan esa respuesta.
Estructuras de datos clásicas
[editar]Algunas estructuras empleadas en la resolución de problemas de forma eficiente:
- Diagrama de Voronoi : Dado un conjunto de puntos, crear una partición del plano de acuerdo al punto más cercano.
- Triangulación de Delaunay : Dado un conjunto de puntos, crear la mejor triangulación para interpolar valores en su interior.
- Octree y Árbol kd : Organizar el espacio para realizar búsquedas geométricas de forma efectiva.
Geometría computacional numérica
[editar]
Esta rama también llamada geometría máquina, diseño geométrico asistido por computador (CAGD), o modelado geométrico, trata principalmente del estudio de modelado y representación de curvas y superficies por ordenador. Para ello, emplea elementos como curvas y superficies paramétricas, (tipo curvas de Bézier o Splines) o curvas no paramétricas (como conjuntos de nivel).
Las áreas de aplicación incluyen industrias como diseño de naves, aeronaves y automóviles, diseño de escenarios y personajes de videojuegos, o animación por computadora, entre otras.
Bibliografía
[editar]https://personal.us.es/almar/docencia/practicas/
Referencias y enlaces externos
[editar]- ↑ a b Shamos, Michael (1978). «Computational Geometry» (PDF). Yale University.
- ↑ Franco P. Preparata and Michael Ian Shamos (1985). Computational Geometry - An Introduction. Springer-Verlag. 1st edition: ISBN 0-387-96131-3; 2nd printing, corrected and expanded, 1988: ISBN 3-540-96131-3.
- ↑ Forrest, A. (1971). «Computational geometry». Proc. Royal Society London 321 (1545). doi:10.1098/rspa.1971.0025.
- ↑ Khuller, Samir; Matias, Y. (1995). «A simple randomized sieve algorithm for the closest-pair problem». Information and Computation 118 (1): 34-37. doi:10.1006/inco.1995.1049.
- ↑ Fortune, Steve; Hopcroft, J.E. (1979). «A note on Rabin's nearest-neighbor algorithm». Information Processing Letters 8 (1): 20-23.
- ↑ Morales, Miguel Ángel (27 de junio de 2011). «Una interesante introducción a la Geometría Computacional». Gaussianos. Consultado el 1 de marzo de 2017.
- ↑ Rivero, Francisco. «Geometría Computacional». Consultado el 1 de marzo de 2017.
- ↑ Grima, Clara (2011). «Cada uno en su región y Voronoi en la de todos». Naukas.
- ↑ O'Rourke, Joseph. Computational Geometry in C (2 edición). Cambridge University Press. ISBN 9780521649766.
Otros recursos
[editar] Wikimedia Commons alberga una categoría multimedia sobre Geometría computacional.
Wikimedia Commons alberga una categoría multimedia sobre Geometría computacional.- «Journal of Computational Geometry». Consultado el 1 de marzo de 2017.
- «International Symposium on Computational Geometry». Consultado el 1 de marzo de 2017.
- The Computational Geometry Algorithms Library (CGAL)
