Diferencia entre revisiones de «Efecto Zeeman»
mSin resumen de edición |
Creado al traducir la página «Zeeman effect» |
||
| Línea 1: | Línea 1: | ||
| ⚫ | [[Archivo:ZeemanEffectIllus.png|miniaturadeimagen| Las líneas espectrales de la lámpara de vapor de mercurio |
||
| ⚫ | |||
[[File:Explanation_of_how_the_magnetic_field_on_a_star_affects_the_light_emitted.webm|miniaturadeimagen|<small>Esta animación muestra lo que sucede cuando se forma una mancha solar (o una mancha estelar) y el campo magnético aumenta su fuerza. La luz que emerge del lugar comienza a demostrar el efecto Zeeman. Las líneas de espectro oscuro en el espectro de la luz emitida se dividen en tres componentes y la fuerza de la polarización circular en partes del espectro aumenta significativamente. Este efecto de polarización es una herramienta poderosa para que los astrónomos detecten y midan los campos magnéticos estelares.</small>]] |
|||
| ⚫ | El '''efecto Zeeman''' |
||
| ⚫ | [[Archivo:ZeemanEffectIllus.png|miniaturadeimagen| Las líneas espectrales de la lámpara de vapor de mercurio en la longitud de onda 546.1 nm, mostrando un efecto Zeeman anómalo. (A) Sin campo magnético. (SEGUNDO) Con el campo magnético, las líneas espectrales se dividen como un efecto Zeeman transversal. (C) Con campo magnético, dividido como efecto Zeeman longitudinal. Las líneas espectrales se obtuvieron mediante un [[Interferómetro Fabry-Pérot|interferómetro de Fabry-Pérot]].]] |
||
| ⚫ | Dado que la distancia entre los subniveles de Zeeman es una función de la intensidad del campo magnético, este efecto se puede utilizar para medir la intensidad del campo magnético, por ejemplo, |
||
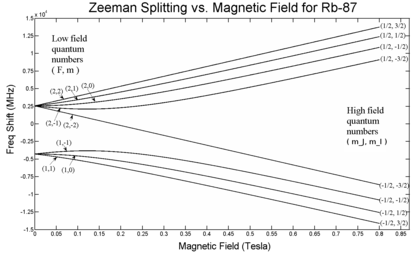
| ⚫ | [[Archivo:Breit-rabi-Zeeman.png|miniaturadeimagen|420x420px| División de Zeeman del nivel 5 de [[Rubidio|{{Exp|87}}Rb]], incluida la división de estructura fina y estructura hiperfina. Aquí ''F'' = ''J'' + ''I'', donde ''I'' es el espín nuclear (para {{Exp|87}}Rb, ''I'' = {{frac|3|2}})]] |
||
[[File:Explanation_of_how_the_magnetic_field_on_a_star_affects_the_light_emitted.webm|miniaturadeimagen|<small>This animation shows what happens as a sunspot (or starspot) forms and the magnetic field increases in strength. The light emerging from the spot starts to demonstrate the Zeeman effect. The dark spectra lines in the spectrum of the emitted light split into three components and the strength of the circular polarisation in parts of the spectrum increases significantly. This polarisation effect is a powerful tool for astronomers to detect and measure stellar magnetic fields.</small>]] |
|||
| ⚫ | El '''efecto Zeeman''', que lleva el nombre del físico [[Países Bajos|neerlandés]] [[Pieter Zeeman]], es el efecto de la división de una [[línea espectral]] en varios componentes en presencia de un [[campo magnético]] estático. Es análogo al [[efecto Stark]], la división de una línea espectral en varios componentes en presencia de un [[campo eléctrico]]. También similar al efecto Stark, las transiciones entre diferentes componentes tienen, en general, diferentes intensidades, estando algunas totalmente prohibidas (en la aproximación [[dipolo eléctrico|dipolar]]), según se rige por las [[Regla de selección|reglas de selección]]. |
||
| ⚫ | Dado que la distancia entre los subniveles de Zeeman es una función de la intensidad del campo magnético, este efecto se puede utilizar para medir la intensidad del campo magnético, por ejemplo, el del [[Sol]] y otras [[Estrella|estrellas]] o en [[Plasma (estado de la materia)|plasmas]] de laboratorio. El efecto Zeeman es muy importante en aplicaciones como la [[Resonancia magnética nuclear|espectroscopia de resonancia magnética nuclear]], la espectroscopia de [[Resonancia paramagnética electrónica|resonancia de espín electrónico]], la [[Imagen por resonancia magnética|formación de imágenes por resonancia magnética]] (MRI) y la [[Espectroscopia Mössbauer|espectroscopia de Mössbauer]]. También se puede utilizar para mejorar la precisión en la [[Espectroscopia de absorción atómica (AA)|espectroscopia de absorción atómica]]. Una teoría sobre el [[Magnetorrecepción|sentido magnético]] de las aves asume que una proteína en la retina cambia debido al efecto Zeeman. <ref>{{Cita publicación|título=The magnetic compass mechanisms of birds and rodents are based on different physical principles|apellidos=Thalau|nombre=Peter|apellidos2=Ritz|nombre2=Thorsten|fecha=18 April 2006|publicación=Journal of the Royal Society Interface|volumen=3|número=9|páginas=583–587|doi=10.1098/rsif.2006.0130|pmc=1664646|pmid=16849254|apellidos3=Burda|nombre3=Hynek|apellidos4=Wegner|nombre4=Regina E.|apellidos5=Wiltschko|nombre5=Roswitha}}</ref> |
||
| ⚫ | |||
| ⚫ | |||
== Nomenclatura == |
== Nomenclatura == |
||
Históricamente, se distingue entre el '''efecto Zeeman''' '''normal''' y |
Históricamente, se distingue entre el '''efecto Zeeman''' '''normal''' y '''anómalo''' (descubierto por [[Thomas Preston]] en Dublín, Irlanda <ref>{{Cita publicación|url=https://babel.hathitrust.org/cgi/pt?id=mdp.39015035446916;view=1up;seq=481|título=Radiation phenomena in a strong magnetic field|apellidos=Preston|nombre=Thomas|fecha=1898|publicación=The Scientific Transactions of the Royal Dublin Society|volumen=6|páginas=385–342|serie=2nd series}}</ref> ). El efecto anómalo aparece en las transiciones en las que el spin neto de los [[Electrón|electrones]] no es cero. Se le llamó "anómalo" porque el espín del electrón aún no se había descubierto, por lo que no había una buena explicación en el momento en que Zeeman observó el efecto. |
||
A mayor intensidad de campo magnético, el efecto deja de ser lineal. A una fuerza de campo aún mayor, cuando la fuerza del campo externo es comparable a la fuerza del campo interno del átomo, el acoplamiento de electrones se altera y las líneas espectrales se reorganizan. Esto se llama [[Efecto Zeeman|'''efecto Paschen-Back''']]. |
|||
En la literatura científica moderna, estos términos |
En la literatura científica moderna, estos términos se utilizan raramente, con una tendencia a utilizar solo "efecto Zeeman". |
||
== Presentación teórica == |
== Presentación teórica == |
||
El [[Hamiltoniano (mecánica cuántica)| |
El [[Hamiltoniano (mecánica cuántica)|hamiltoniano]] total de un átomo en un campo magnético es |
||
: <math>H = H_0 + |
: <math>H = H_0 + V_{\rm M},\ </math> |
||
donde <math>H_0</math> es el hamiltoniano imperturbable del átomo, y <math>V_{\rm M}</math> es la [[Teoría perturbacional|perturbación]] debida al campo magnético: |
|||
: <math> |
: <math>V_{\rm M} = -\vec{\mu} \cdot \vec{B},</math> |
||
donde <math>\vec{\mu}</math> es el [[momento magnético]] del átomo. El momento magnético consta de las partes electrónicas y nucleares; sin embargo, este último es muchos órdenes de magnitud más pequeño y se pasará por alto aquí. Por lo tanto, |
|||
: <math>\vec{\mu} \approx -\frac{\ |
: <math>\vec{\mu} \approx -\frac{\mu_{\rm B} g \vec{J}}{\hbar},</math> |
||
donde <math>\mu_{\rm B}</math> es el [[magnetón de Bohr]], <math>\vec{J}</math> es el [[momento angular]] electrónico total, y <math>g</math> es el [[Factor de Landé|factor g de Landé]]. Un enfoque más preciso es tener en cuenta que el operador del momento magnético de un electrón es una suma de las contribuciones del [[Momento angular en mecánica cuántica|momento angular orbital]] <math>\vec L</math> y el [[Momento angular en mecánica cuántica|momento angular de giro]] <math>\vec S</math>, con cada uno multiplicado por la [[Relación giromagnética|proporción giromagnética]] apropiada: |
|||
: <math>\vec{\mu} = -\frac{\ |
: <math>\vec{\mu} = -\frac{\mu_{\rm B} (g_l \vec{L} + g_s \vec{S})}{\hbar},</math> |
||
donde <math>g_l = 1</math> y <math>g_s \approx 2.0023192</math> (este último se llama [[Momento dipolar magnético anómalo|relación giromagnética anómala]]; la desviación del valor de 2 se debe a los efectos de la [[electrodinámica cuántica]]). En el caso del [[Acoplamiento de momento angular|acoplamiento LS]], se pueden sumar todos los electrones del átomo: |
|||
: <math>g \vec{J} = \left\langle\sum_i (g_l \vec{l_i} + g_s \vec{s_i})\right\rangle = \left\langle (g_l\vec{L} + g_s \vec{S})\right\rangle,</math> |
: <math>g \vec{J} = \left\langle\sum_i (g_l \vec{l_i} + g_s \vec{s_i})\right\rangle = \left\langle (g_l\vec{L} + g_s \vec{S})\right\rangle,</math> |
||
donde <math>\vec{L}</math> y <math>\vec{S}</math> son el momento orbital total y el spin del átomo, y el promedio se realiza sobre un estado con un valor dado del momento angular total. |
|||
Si el término de interacción <math>V_M</math> es pequeño (menos que la [[ |
Si el término de interacción <math>V_M</math> es pequeño (menos que la [[estructura fina]]), puede tratarse como una perturbación; este es el efecto Zeeman propiamente dicho. En el efecto Paschen-Back, que se describe a continuación, <math>V_M</math> excede el [[Acoplamiento de momento angular|acoplamiento LS]] significativamente (pero aún es pequeño en comparación con <math>H_{0}</math>). En campos magnéticos ultrafuertes, la interacción del campo magnético puede exceder <math>H_0</math>, en cuyo caso el átomo ya no puede existir en su significado normal, y en su lugar se habla de [[Cuantización de Landau|niveles de Landau]]. Hay casos intermedios que son más complejos que estos casos límite. |
||
== Campo débil (efecto Zeeman) == |
== Campo débil (efecto Zeeman) == |
||
Si la [[ |
Si la [[Interacción giro-órbita|interacción espín-órbita]] domina sobre el efecto del campo magnético externo, <math>\scriptstyle \vec L</math> y <math>\scriptstyle \vec S</math> no se conservan por separado, solo el momento angular total <math>\scriptstyle \vec J = \vec L + \vec S</math> es. Se puede pensar que los vectores de momento angular orbital y de espín precesan alrededor del vector de momento angular total (fijo) <math>\scriptstyle \vec J</math>. El vector de giro (tiempo-) "promediado" es entonces la proyección del giro en la dirección de <math>\scriptstyle \vec J</math>: |
||
: <math>\vec S_{avg} = \frac{(\vec S \cdot \vec J)}{J^2} \vec J</math> |
: <math>\vec S_{\rm avg} = \frac{(\vec S \cdot \vec J)}{J^2} \vec J</math> |
||
y para el vector orbital "promediado": |
y para el vector orbital (tiempo -) "promediado": |
||
: <math>\vec L_{avg} = \frac{(\vec L \cdot \vec J)}{J^2} \vec J.</math> |
: <math>\vec L_{\rm avg} = \frac{(\vec L \cdot \vec J)}{J^2} \vec J.</math> |
||
Por lo tanto, |
|||
Así, |
|||
: <math>\langle |
: <math>\langle V_{\rm M} \rangle = \frac{\mu_{\rm B}}{\hbar} \vec J\left(g_L\frac{\vec L \cdot \vec J}{J^2} + g_S\frac{\vec S \cdot \vec J}{J^2}\right) \cdot \vec B.</math> |
||
Usando <math>\scriptstyle \vec L = \vec J - \vec S</math> y cuadrando ambos lados, obtenemos |
|||
: <math>\vec S \cdot \vec J = \frac{1}{2}(J^2 + S^2 - L^2) = \frac{\hbar^2}{2}[j(j+1) - l(l+1) + s(s+1)],</math> |
: <math>\vec S \cdot \vec J = \frac{1}{2}(J^2 + S^2 - L^2) = \frac{\hbar^2}{2}[j(j+1) - l(l+1) + s(s+1)],</math> |
||
y: usando |
y: usando <math>\scriptstyle \vec S = \vec J - \vec L</math> y cuadrando ambos lados, obtenemos |
||
: <math>\vec L \cdot \vec J = \frac{1}{2}(J^2 - S^2 + L^2) = \frac{\hbar^2}{2}[j(j+1) + l(l+1) - s(s+1)].</math> |
: <math>\vec L \cdot \vec J = \frac{1}{2}(J^2 - S^2 + L^2) = \frac{\hbar^2}{2}[j(j+1) + l(l+1) - s(s+1)].</math> |
||
Combinando todo y tomando |
Combinando todo y tomando <math>\scriptstyle J_z = \hbar m_j</math>, obtenemos la energía potencial magnética del átomo en el campo magnético externo aplicado, |
||
: <math> |
: <math> |
||
\begin{align} |
\begin{align} |
||
V_{\rm M} |
|||
V_M |
|||
&= \ |
&= \mu_{\rm B} B m_j \left[ g_L\frac{j(j+1) + l(l+1) - s(s+1)}{2j(j+1)} + g_S\frac{j(j+1) - l(l+1) + s(s+1)}{2j(j+1)} \right]\\ |
||
&= \ |
&= \mu_{\rm B} B m_j \left[1 + (g_S-1)\frac{j(j+1) - l(l+1) + s(s+1)}{2j(j+1)} \right], |
||
\\ |
\\ |
||
&= \ |
&= \mu_{\rm B} B m_j g_j |
||
\end{align} |
\end{align} |
||
</math> |
</math> |
||
donde la cantidad entre corchetes es el [[Factor de Landé|factor g |
donde la cantidad entre corchetes es el [[Factor de Landé|factor g Landé]] g<sub>J</sub> del átomo (<math>g_L = 1</math> y <math>g_S \approx 2</math>) y <math>m_j</math> es la componente z del momento angular total. Por un solo electrón por encima de las capas llenas <math>s = 1/2</math> y <math> j = l \pm s </math>, el factor g de Landé se puede simplificar en: |
||
: <math> g_j = 1 \pm \frac{g_S-1}{2l+1} </math> |
: <math> g_j = 1 \pm \frac{g_S-1}{2l+1} </math> |
||
Tomando |
Tomando <math>V_m</math> para ser la perturbación, la corrección de Zeeman a la energía es |
||
: <math> |
: <math> |
||
\begin{align} |
\begin{align} |
||
E_{\rm Z}^{(1)} = \langle n l j m_j | H_{\rm Z}^' | n l j m_j \rangle = \langle V_M \rangle_\Psi = \mu_{\rm B} g_J B_{\rm ext} m_j |
|||
\end{align} |
\end{align} |
||
</math> |
</math> |
||
=== Ejemplo: transición |
=== Ejemplo: transición Lyman-alfa en hidrógeno === |
||
La |
La [[Línea Lyman-alfa|transición Lyman-alfa]] en [[hidrógeno]] en presencia de la [[Interacción giro-órbita|interacción espín-órbita]] implica las transiciones |
||
: <math>2P_{1/2} \to 1S_{1/2}</math> y <math>2P_{3/2} \to 1S_{1/2}.</math> |
: <math>2P_{1/2} \to 1S_{1/2}</math> y <math>2P_{3/2} \to 1S_{1/2}.</math> |
||
En presencia de un campo magnético externo, el efecto Zeeman de campo débil divide los niveles 1S |
En presencia de un campo magnético externo, el efecto Zeeman de campo débil divide los niveles 1S<sub>1/2</sub> y 2P<sub>1/2</sub> en 2 estados cada uno (<math>m_j = 1/2, -1/2</math>) y el nivel 2P<sub>3/2</sub> en 4 estados (<math>m_j = 3/2, 1/2, -1/2, -3/2</math>). Los factores g de Landé para los tres niveles son: |
||
: <math>g_J = 2</math> |
: <math>g_J = 2</math> por <math>1S_{1/2}</math> (j = 1/2, l = 0) |
||
: <math>g_J = 2/3</math> |
: <math>g_J = 2/3</math> por <math>2P_{1/2}</math> (j = 1/2, l = 1) |
||
: <math>g_J = 4/3</math> |
: <math>g_J = 4/3</math> por <math>2P_{3/2}</math> (j = 3/2, l = 1). |
||
Tenga en cuenta en particular que el tamaño de la división de energía es diferente para los diferentes orbitales, porque los valores de g<sub>J</sub> son diferentes. |
Tenga en cuenta en particular que el tamaño de la división de energía es diferente para los diferentes orbitales, porque los valores de g<sub>J</sub> son diferentes. A la izquierda, se muestra una fina estructura dividida. Esta división ocurre incluso en ausencia de un campo magnético, ya que se debe al acoplamiento espín-órbita. Representado a la derecha es la división adicional de Zeeman, que ocurre en presencia de campos magnéticos. |
||
[[File:Zeeman_p_s_doublet.svg|400x400px]] |
|||
{| class="wikitable" |
{| class="wikitable" |
||
|+Posibles transiciones |
|+Posibles transiciones para el efecto Zeeman débil |
||
!Estado inicial |
! Estado inicial |
||
(<math>n=2,l=1</math>) |
( <math>n=2,l=1</math> ) |
||
<math>\mid j, m_{j}\rangle</math> |
<math>\mid j, m_{j}\rangle</math> |
||
| ⚫ | |||
| ⚫ | |||
| ⚫ | |||
| ⚫ | |||
| ⚫ | |||
<math>\mid j, m_{j}\rangle</math> |
<math>\mid j, m_{j}\rangle</math> |
||
| ⚫ | |||
|- |
|- |
||
|<math>\ |
| <math> \left| \frac{1}{2}, \pm\frac{1}{2} \right\rangle </math> |
||
|<math>\ |
| <math> \left| \frac{1}{2}, \pm\frac{1}{2} \right\rangle </math> |
||
|<math> |
| <math> \mp\frac{2}{3} \mu_{\rm B}B </math> |
||
|- |
|- |
||
|<math>\ |
| <math> \left| \frac{1}{2}, \pm\frac{1}{2} \right\rangle </math> |
||
|<math> |
| <math> \left| \frac{1}{2}, \mp\frac{1}{2} \right\rangle </math> |
||
|<math> |
| <math> \pm\frac{4}{3} \mu_{\rm B}B </math> |
||
|- |
|- |
||
|<math>\ |
| <math> \left| \frac{3}{2}, \pm\frac{3}{2} \right\rangle </math> |
||
|<math> |
| <math> \left| \frac{1}{2}, \pm\frac{1}{2} \right\rangle </math> |
||
|<math>\ |
| <math> \pm \mu_{\rm B}B </math> |
||
|- |
|- |
||
|<math>\ |
| <math> \left| \frac{3}{2}, \pm\frac{1}{2} \right\rangle </math> |
||
|<math> |
| <math> \left| \frac{1}{2}, \pm\frac{1}{2} \right\rangle </math> |
||
|<math> |
| <math> \mp\frac{1}{3} \mu_{\rm B}B </math> |
||
|- |
|- |
||
|<math>\ |
| <math> \left| \frac{3}{2}, \pm\frac{1}{2} \right\rangle </math> |
||
|<math> |
| <math> \left| \frac{1}{2}, \mp\frac{1}{2} \right\rangle </math> |
||
|<math> |
| <math> \pm\frac{5}{3} \mu_{\rm B}B </math> |
||
|} |
|} |
||
== Campo fuerte (efecto Paschen-Back) == |
== Campo fuerte (efecto Paschen-Back) == |
||
El efecto Paschen-Back es la división de los niveles de energía atómica en presencia de un fuerte campo magnético. |
El efecto Paschen-Back es la división de los niveles de energía atómica en presencia de un fuerte campo magnético. Esto ocurre cuando un campo magnético externo es lo suficientemente fuerte como para interrumpir el acoplamiento entre orbitales (<math>\vec{L}</math>) y girar (<math>\vec{S}</math>) momentos angulares. Este efecto es el límite de campo fuerte del efecto Zeeman. Cuando <math>s = 0</math>, los dos efectos son equivalentes. El efecto lleva el nombre de los [[Físico|físicos]] [[Alemania|alemanes]] [[Friedrich Paschen]] y [[Ernst Back|Ernst E. A. Back]]. <ref>{{Cita publicación|título=Liniengruppen magnetisch vervollständigt|apellidos=Paschen|nombre=F.|apellidos2=Back|nombre2=E.|fecha=1921|publicación=Physica|volumen=1|páginas=261–273|idioma=German|títulotrad=Line groups magnetically completed [i.e., completely resolved]}} Available at: [https://www.lorentz.leidenuniv.nl/history/proefschriften/Physica/Physica_1_1921_05391.pdf Leiden University (Netherlands)]</ref> |
||
Cuando la perturbación del campo magnético excede significativamente la interacción espín-órbita, |
Cuando la perturbación del campo magnético excede significativamente la interacción espín-órbita, se puede asumir con seguridad <math>[H_{0}, S] = 0</math>. Esto permite que los valores esperados de <math>L_{z}</math> y <math>S_{z}</math> para ser fácilmente evaluado por un estado <math>|\psi\rangle </math>. Las energías son simplemente |
||
: <math> E_{z} = \left\langle \psi \left| H_{0} + \frac{B_{z}\ |
: <math> E_{z} = \left\langle \psi \left| H_{0} + \frac{B_{z}\mu_{\rm B}}{\hbar}(L_{z}+g_{s}S_z) \right|\psi\right\rangle = E_{0} + B_z\mu_{\rm B} (m_l + g_{s}m_s). </math> |
||
Lo anterior puede interpretarse como implicando que el acoplamiento LS está completamente roto por el campo externo. Sin embargo <math>m_l</math> y <math>m_s</math> siguen siendo números cuánticos "buenos". Junto con las [[Regla de selección|reglas de selección]] para una [[Transición dipolo eléctrico|transición de dipolo eléctrico]], es decir, <math>\Delta s = 0, \Delta m_s = 0, \Delta l = \pm 1, \Delta m_l = 0, \pm 1</math> esto permite ignorar por completo el grado de libertad de giro. Como resultado, solo tres líneas espectrales serán visibles, correspondientes a la <math>\Delta m_l = 0, \pm 1</math> regla de selección. La división <math>\Delta E = B \mu_{\rm B} \Delta m_l</math> es ''independiente'' de las energías no perturbadas y las configuraciones electrónicas de los niveles considerados. En general (si <math>s \ne 0</math>), estos tres componentes son en realidad grupos de varias transiciones cada uno, debido al acoplamiento de espín-órbita residual. |
|||
En general, ahora se debe agregar el acoplamiento de |
En general, ahora se debe agregar el acoplamiento de espín-órbita y las correcciones relativistas (que son del mismo orden, conocidas como "estructura fina") como una perturbación a estos niveles "imperturbables". La teoría de perturbación de primer orden con estas correcciones de estructura fina produce la siguiente fórmula para el átomo de hidrógeno en el límite de Paschen – Back: <ref>{{Cita libro|apellidos=Griffiths, David J.|título=Introduction to Quantum Mechanics|edición=2nd|editorial=[[Prentice Hall]]|fecha=2004|isbn=0-13-111892-7|oclc=40251748|página=247}}</ref> |
||
: <math> E_{z+fs} = E_{z} + \frac{m_e c^2 \alpha^4}{2 n^3} \left\{ \frac{3}{4n} - \left[ \frac{l(l+1) - m_l m_s}{l(l+1/2)(l+1) } \right]\right\}.</math> |
: <math> E_{z+fs} = E_{z} + \frac{m_e c^2 \alpha^4}{2 n^3} \left\{ \frac{3}{4n} - \left[ \frac{l(l+1) - m_l m_s}{l(l+1/2)(l+1) } \right]\right\}.</math> |
||
| Línea 149: | Línea 148: | ||
{| class="wikitable" |
{| class="wikitable" |
||
|+Posibles transiciones |
|+Posibles transiciones Lyman-alfa para el régimen fuerte |
||
!Estado inicial |
! Estado inicial |
||
(<math>n=2,l=1</math>) |
( <math>n=2,l=1</math> ) |
||
<math>\mid m_l, m_{s}\rangle</math> |
<math>\mid m_l, m_{s}\rangle</math> |
||
! |
! Perturbación energética inicial |
||
!Estado final |
! Estado final |
||
(<math>n=1,l=0</math>) |
( <math>n=1,l=0</math> ) |
||
<math>\mid m_l, m_{s}\rangle</math> |
<math>\mid m_l, m_{s}\rangle</math> |
||
|- |
|- |
||
|<math>\ |
| <math>\left| 1, \frac{1}{2}\right\rangle</math> |
||
|<math>\pm2\mu_{B}B_{z}</math> |
| <math>\pm2\mu_{\rm B}B_{z}</math> |
||
|<math>\ |
| <math>\left| 0, \frac{1}{2}\right\rangle</math> |
||
|- |
|- |
||
|<math>\ |
| <math>\left| 0, \frac{1}{2}\right\rangle</math> |
||
|<math>+\mu_{B}B_{z} </math> |
| <math>+\mu_{\rm B}B_{z} </math> |
||
|<math>\ |
| <math>\left| 0, \frac{1}{2}\right\rangle</math> |
||
|- |
|- |
||
|<math>\ |
| <math>\left| 1, -\frac{1}{2}\right\rangle</math> |
||
|<math>0 </math> |
| <math>0 </math> |
||
|<math>\ |
| <math>\left| 0, -\frac{1}{2}\right\rangle</math> |
||
|- |
|- |
||
|<math>\ |
| <math>\left| -1, \frac{1}{2}\right\rangle</math> |
||
|<math>0 </math> |
| <math>0 </math> |
||
|<math>\ |
| <math>\left| 0, \frac{1}{2}\right\rangle</math> |
||
|- |
|- |
||
|<math>\ |
| <math>\left| 0, -\frac{1}{2}\right\rangle</math> |
||
|<math>-\mu_{B}B_{z} </math> |
| <math>-\mu_{\rm B}B_{z} </math> |
||
|<math>\ |
| <math>\left| 0, -\frac{1}{2}\right\rangle</math> |
||
|- |
|- |
||
|<math>\ |
| <math>\left| -1, -\frac{1}{2}\right\rangle</math> |
||
|<math>-2\mu_{B}B_{z} </math> |
| <math>-2\mu_{\rm B}B_{z} </math> |
||
|<math>\ |
| <math>\left| 0, -\frac{1}{2}\right\rangle</math> |
||
|} |
|} |
||
: |
|||
== Campo intermedio para j = 1/2 == |
== Campo intermedio para j = 1/2 == |
||
En la aproximación del dipolo magnético, el |
En la aproximación del dipolo magnético, el hamiltoniano que incluye las interacciones [[Transición hiperfina|hiperfina]] y de Zeeman es |
||
: <math> H = h A \vec I \cdot \vec J |
: <math> H = h A \vec I \cdot \vec J - \vec \mu \cdot \vec B </math> |
||
: <math> H = h A \vec I \cdot\vec J + ( \ |
: <math> H = h A \vec I \cdot\vec J + ( \mu_{\rm B} g_J\vec J + \mu_{\rm N} g_I\vec I ) \cdot \vec {\rm B} </math> |
||
donde <math>A</math> es la división hiperfina (en Hz) en el campo magnético aplicado cero, <math>\mu_{\rm B}</math> y <math>\mu_{\rm N}</math> son el [[magnetón de Bohr]] y [[Magnetón nuclear|el magnetón nuclear]] respectivamente, <math>\vec J</math> y <math>\vec I</math> son los operadores de momento angular de electrones y nucleares y <math>g_J</math> es el [[Factor de Landé|factor g de Landé:]] |
|||
: <math> g_J = g_L\frac{J(J+1) + L(L+1) - S(S+1)}{2J(J+1)} + g_S\frac{J(J+1) - L(L+1) + S(S+1)}{2J(J+1)}</math>. |
: <math> g_J = g_L\frac{J(J+1) + L(L+1) - S(S+1)}{2J(J+1)} + g_S\frac{J(J+1) - L(L+1) + S(S+1)}{2J(J+1)}</math> . |
||
En el caso de campos magnéticos débiles, la interacción |
En el caso de campos magnéticos débiles, la interacción Zeeman puede tratarse como una perturbación del <math>|F,m_f \rangle</math> base. En el régimen de campo alto, el campo magnético se vuelve tan fuerte que dominará el efecto Zeeman, y uno debe usar una base más completa de <math>|I,J,m_I,m_J\rangle</math> o solo <math>|m_I,m_J \rangle</math>, ya que <math>I</math> y <math>J</math> será constante dentro de un nivel dado. |
||
Para obtener una imagen completa, incluidas las intensidades de campo intermedias, debemos considerar los estados propios que son superposiciones de <math>|F,m_F \rangle </math>y <math>|m_I,m_J \rangle </math> estados base |
Para obtener una imagen completa, incluidas las intensidades de campo intermedias, debemos considerar los estados propios que son superposiciones de <math>|F,m_F \rangle </math> y <math>|m_I,m_J \rangle </math> estados base. Para <math>J = 1/2</math>, el hamiltoniano se puede resolver analíticamente, dando como resultado la fórmula Breit-Rabi. En particular, la interacción cuadrupolo eléctrico es cero para <math>L = 0</math> (<math>J = 1/2</math>), por lo que esta fórmula es bastante precisa. |
||
Para resolver este sistema, notamos que en todo momento, la proyección de momento angular total <math>m_F = m_J + m_I</math>se conservará. Además, desde <math>J = 1/2</math>entre estados <math>m_J</math> cambiará entre solo <math>\pm 1/2</math>. Por lo tanto, podemos definir una buena base como: |
|||
: <math>|\pm\rangle \equiv |m_J = \pm 1/2, m_I = m_F \mp 1/2 \rangle </math> |
|||
Ahora utilizamos [[Operador escalera|operadores de escalera]] mecánica cuántica, que se definen para un operador de momento angular general |
Ahora utilizamos [[Operador escalera|operadores de escalera]] mecánica cuántica, que se definen para un operador de momento angular general <math>L</math> como |
||
: <math> L_{\pm} \equiv L_x \pm iL_y </math> |
: <math> L_{\pm} \equiv L_x \pm iL_y </math> |
||
Estos operadores de escalera tienen la propiedad |
Estos operadores de escalera tienen la propiedad |
||
: <math> L_{\pm}|L_,m_L \rangle = \sqrt{(L \mp m_L)(L \pm m_L +1)} |L,m_L \pm 1 \rangle</math> |
: <math> L_{\pm}|L_,m_L \rangle = \sqrt{(L \mp m_L)(L \pm m_L +1)} |L,m_L \pm 1 \rangle</math> |
||
siempre |
siempre y cuando <math>m_L</math> se encuentra en el rango <math>{-L, \dots ... ,L}</math> (de lo contrario, devuelven cero). Usando operadores de escalera <math>J_{\pm}</math> y <math>I_{\pm}</math> podemos reescribir el hamiltoniano como |
||
: <math> H = h A I_z J_z + \frac{hA}{2}(J_+ I_- + J_- I_+) + \ |
: <math> H = h A I_z J_z + \frac{hA}{2}(J_+ I_- + J_- I_+) + \mu_{\rm B} B g_J J_z + \mu_{\rm N} B g_I I_z</math> |
||
Ahora podemos ver que en todo momento, la proyección del momento angular total <math>m_F = m_J + m_I</math> se conservará. Esto es porque ambos <math>J_z</math> y <math>I_z</math> dejar estados con definidas <math> m_J </math> y <math> m_I </math> sin cambios, mientras <math> J_+ I_- </math> y <math> J_- I_+ </math> o bien aumentar <math> m_J </math> y disminuir <math> m_I </math> o viceversa, por lo que la suma siempre no se ve afectada. Además, dado que <math>J = 1/2</math> solo hay dos valores posibles de <math>m_J</math> las cuales son <math>\pm 1/2</math>. Por lo tanto, para cada valor de <math> m_F </math> solo hay dos estados posibles, y podemos definirlos como base: |
|||
| ⚫ | |||
: <math> |
: <math>|\pm\rangle \equiv |m_J = \pm 1/2, m_I = m_F \mp 1/2 \rangle </math> |
||
| ⚫ | |||
: <math> \langle \pm |H|\pm \rangle = -\frac{1}{4} hA + \mu_{\rm N} B g_I m_F \pm \frac{1}{2} (hAm_F + \mu_{\rm B} B g_J- \mu_{\rm N} B g_I))</math> |
|||
: <math> \langle \pm |H| \mp \rangle = \frac{1}{2} hA \sqrt{(I + 1/2)^2 - m_F^2}</math> |
: <math> \langle \pm |H| \mp \rangle = \frac{1}{2} hA \sqrt{(I + 1/2)^2 - m_F^2}</math> |
||
Resolviendo los valores propios de esta matriz, (como se puede hacer a mano |
Resolviendo los valores propios de esta matriz, (como se puede hacer a mano o más fácilmente, con un sistema de álgebra por computadora) llegamos a los cambios de energía: |
||
: <math> \Delta E_{F=I\pm1/2} = |
: <math> \Delta E_{F=I\pm1/2} = -\frac{h \Delta W }{2(2I+1)} + \mu_{\rm N} g_I m_F B \pm \frac{h \Delta W}{2}\sqrt{1 + \frac{2m_F x }{I+1/2}+ x^2 }</math> |
||
: <math>x \equiv \frac{\ |
: <math>x \equiv \frac{B(\mu_{\rm B} g_J - \mu_{\rm N} g_I)}{h \Delta W} \quad \quad \Delta W= A \left(I+\frac{1}{2}\right)</math> |
||
donde <math>\Delta W</math>es la división (en unidades de Hz) entre dos subniveles hiperfinos en ausencia de campo magnético <math>B</math>, <math>x</math>se conoce como el 'parámetro de intensidad de campo' (Nota: para |
donde <math>\Delta W</math> es la división (en unidades de Hz) entre dos subniveles hiperfinos en ausencia de campo magnético <math>B</math>, <math>x</math> se conoce como el 'parámetro de intensidad de campo' (Nota: para <math>m_F = \pm(I+1/2)</math> la expresión debajo de la raíz cuadrada es un cuadrado exacto, por lo que el último término debe reemplazarse por <math>+\frac{h\Delta W}{2}(1\pm x)</math>). Esta ecuación se conoce como '''fórmula Breit-Rabi''' y es útil para sistemas con un electrón de valencia en un <math>s</math> (<math>J = 1/2</math>) nivel. <ref>{{Cita libro|apellidos=Woodgate|nombre=Gordon Kemble|título=Elementary Atomic Structure|fecha=1980|editorial=Oxford University Press|ubicación=Oxford, England|páginas=193–194|edición=2nd}}</ref> <ref>First appeared in: {{Cita publicación|título=Measurement of nuclear spin|apellidos=Breit|nombre=G.|apellidos2=Rabi|nombre2=I.I.|fecha=1931|publicación=Physical Review|volumen=38|número=11|páginas=2082–2083|bibcode=1931PhRv...38.2082B|doi=10.1103/PhysRev.38.2082.2}}</ref> |
||
Tenga en cuenta que el índice <math>F</math>en <math>\Delta E_{F=I\pm1/2}</math>debe considerarse no como |
Tenga en cuenta que el índice <math>F</math> en <math>\Delta E_{F=I\pm1/2}</math> debe considerarse no como momento angular total del átomo, sino como ''momento angular total asintótico''. Es igual al momento angular total solo si <math>B=0</math> de lo contrario, los vectores propios correspondientes a diferentes valores propios del hamiltoniano son las superposiciones de estados con diferentes <math>F</math> pero igual <math>m_F</math> (las únicas excepciones son <math>|F=I+1/2,m_F=\pm F \rangle</math>). |
||
== Aplicaciones == |
== Aplicaciones == |
||
=== Astrofísica === |
=== Astrofísica === |
||
[[Archivo:Sunzeeman1919.png|derecha|miniaturadeimagen|200x200px| Efecto Zeeman |
[[Archivo:Sunzeeman1919.png|derecha|miniaturadeimagen|200x200px| Efecto Zeeman en una línea espectral de manchas solares]] |
||
[[George Ellery Hale]] fue el primero en notar el efecto Zeeman en los espectros solares, lo que indica la existencia de fuertes campos magnéticos en las manchas solares. |
[[George Ellery Hale]] fue el primero en notar el efecto Zeeman en los espectros solares, lo que indica la existencia de fuertes campos magnéticos en las manchas solares. Estos campos pueden ser bastante altos, del orden de 0,1 [[Tesla (unidad)|tesla]] o más. Hoy en día, el efecto Zeeman se utiliza para producir [[Magnetograma|magnetogramas]] que muestran la variación del campo magnético del sol. |
||
=== |
=== Refrigeración por láser === |
||
El efecto Zeeman se utiliza en muchas aplicaciones de [[ |
El efecto Zeeman se utiliza en muchas aplicaciones de [[enfriamiento láser]], como una [[Trampa magneto-óptica|trampa magnetoóptica]] y el [[Zeeman más lento]]. |
||
=== Acoplamiento |
=== Acoplamiento de espín y movimientos orbitales mediado por la energía de Zeeman === |
||
La interacción |
La interacción spin-órbita en los cristales generalmente se atribuye al acoplamiento de matrices de Pauli <math>\boldsymbol{\sigma}</math> al impulso de los electrones <math>\boldsymbol{k}</math> que existe incluso en ausencia de campo magnético <math>\boldsymbol{B}</math> . Sin embargo, bajo las condiciones del efecto Zeeman, cuando <math>{\boldsymbol{B}}\neq 0</math>, se puede lograr una interacción similar acoplando <math>\boldsymbol{\sigma}</math> a la coordenada del electrón <math>\boldsymbol{r}</math> a través de la espacialmente no homogénea Zeeman Hamiltoniana |
||
: <math> |
: <math>H_{\rm Z}=\frac{1}{2}(\boldsymbol{B}{\hat g}\boldsymbol{\sigma})</math> , |
||
donde <math>{\hat g}</math> es un factor ''g'' tensorial de Landé y <math>\boldsymbol{B}=\boldsymbol{B}(\boldsymbol{r})</math> o <math>{\hat g}={\hat g}(\boldsymbol r)</math>, o ambos, dependen de la coordenada del electrón <math>\boldsymbol{r}</math>. Semejante <math>\boldsymbol{r}</math> -dependiente Zeeman Hamiltoniano <math>H_{\rm Z}(\boldsymbol r)</math> parejas de espín de electrones <math>\boldsymbol{\sigma}</math> al operador <math>\boldsymbol{r}</math> que representa el movimiento orbital del electrón. Campo no homogéneo <math>\boldsymbol{B}({\boldsymbol r})</math> puede ser un campo suave de fuentes externas o un campo magnético microscópico de oscilación rápida en antiferromagnetos. <ref>S. I. Pekar and E. I. Rashba, Combined resonance in crystals in inhomogeneous magnetic fields, Sov. Phys. - JETP '''20''', 1295 (1965) http://www.jetp.ac.ru/cgi-bin/dn/e_020_05_1295.pdf</ref> Acoplamiento spin-órbita a través de un campo macroscópicamente no homogéneo <math>\boldsymbol{B}(\boldsymbol{r})</math> de nanoimanes se utiliza para la operación eléctrica de espines de electrones en puntos cuánticos a través de la [[Resonancia de espín dipolo eléctrico|resonancia de espines dipolares eléctricos]], <ref>Y. Tokura, W. G. van der Wiel, T. Obata, and S. Tarucha, Coherent single electron spin control in a slanting Zeeman field, Phys. Rev. Lett. '''96''', 047202 (2006)</ref> y la conducción de espines mediante un campo eléctrico debido a <math>{\hat g}(\boldsymbol r)</math> También se ha demostrado. <ref>{{Cita publicación|url=https://www.semanticscholar.org/paper/f3a7e0c4644cf503881afd52109f54f4c161075d|título=Electrical control of spin coherence in semiconductor nanostructures|apellidos=Salis G, Kato Y, Ensslin K, Driscoll DC, Gossard AC, Awschalom DD|publicación=Nature|volumen=414|número=6864|páginas=619–622|doi=10.1038/414619a|pmid=11740554|año=2001}}</ref> |
|||
== Véase también == |
== Véase también == |
||
* [[ |
* [[efecto Kerr magneto-óptico|Efecto Kerr magneto-óptico]] |
||
* [[ |
* [[Efecto Voigt]] |
||
* [[Efecto Faraday]] |
* [[Efecto Faraday]] |
||
* [[Efecto Cotton-Mouton]] |
* [[Efecto Cotton-Mouton|Efecto algodón-mouton]] |
||
* [[Espectroscopía de polarización]] |
|||
* [[Polarization spectroscopy|Espectroscopia de polarizacion]] |
|||
* [[Energía de Zeeman]] |
* [[Energía de Zeeman|Energía Zeeman]] |
||
* [[Efecto Stark |
* [[Efecto Stark]] |
||
* [[Efecto Lamb| |
* [[Efecto Lamb|Turno de cordero]] |
||
** [[ |
** La [[configuración electrónica]] dice en la subcapa p (l = 1), hay 3 niveles de energía ml = -1,0,1, pero solo vemos dos p1/2 y p3/2, para la subcapa s (l = 0), solo hay 1 nivel de energía (ml = 0), pero aquí tenemos 2. l correspondiente a estructura fina, ml correspondiente a estructura hiperfina. |
||
== Referencias == |
== Referencias == |
||
{{Listaref|30em}} |
|||
<references group="" responsive=""></references> |
|||
=== Histórico === |
=== Histórico === |
||
* {{Cita libro |
* {{Cita libro|nombre=E. U.|apellidos=Condon|apellidos2=G. H. Shortley|título=The Theory of Atomic Spectra|editorial=[[Cambridge University Press]]|fecha=1935|isbn=0-521-09209-4}} ''(Chapter 16 provides a comprehensive treatment, as of 1935.)'' |
||
* {{Cita publicación|url=https://babel.hathitrust.org/cgi/pt?id=uiug.30112109543402;view=1up;seq=201|título=Over de invloed eener magnetisatie op den aard van het door een stof uitgezonden licht|apellidos=Zeeman|nombre=P.|fecha=1896|publicación=Verslagen van de Gewone Vergaderingen der Wis- en Natuurkundige Afdeeling (Koninklijk Akademie van Wetenschappen te Amsterdam) [Reports of the Ordinary Sessions of the Mathematical and Physical Section (Royal Academy of Sciences in Amsterdam)]|volumen=5|páginas=181–184 and 242–248|idioma=Dutch|títulotrad=On the influence of magnetism on the nature of the light emitted by a substance}} |
|||
* {{Cita publicación|título=On the influence of Magnetism on the Nature of the Light emitted by a Substance|apellidos=Zeeman|nombre=P.|fecha=1897|publicación=Phil. Mag.|volumen=43|páginas=226}} {{Cita publicación|título=On the influence of Magnetism on the Nature of the Light emitted by a Substance|apellidos=Zeeman|nombre=P.|fecha=1897|publicación=Phil. Mag.|volumen=43|páginas=226}} {{Cita publicación|título=On the influence of Magnetism on the Nature of the Light emitted by a Substance|apellidos=Zeeman|nombre=P.|fecha=1897|publicación=Phil. Mag.|volumen=43|páginas=226}} {{Cita publicación|título=On the influence of Magnetism on the Nature of the Light emitted by a Substance|apellidos=Zeeman|nombre=P.|fecha=1897|publicación=Phil. Mag.|volumen=43|páginas=226}} ( [https://books.google.com/books?id=fXpDler746QC Google Books] ) |
|||
* {{Cita publicación|url=https://babel.hathitrust.org/cgi/pt?id=mdp.39015024088695;view=1up;seq=238|título=On the influence of magnetism on the nature of the light emitted by a substance|apellidos=Zeeman|nombre=P.|fecha=1897|publicación=Philosophical Magazine|volumen=43|número=262|páginas=226–239|serie=5th series|doi=10.1080/14786449708620985}} |
|||
* {{Cita publicación|título=Doubles and triplets in the spectrum produced by external magnetic forces|apellidos=Zeeman|nombre=P.|fecha=1897|publicación=Phil. Mag.|volumen=44|número=266|páginas=55|doi=10.1080/14786449708621028}} {{Cita publicación|título=Doubles and triplets in the spectrum produced by external magnetic forces|apellidos=Zeeman|nombre=P.|fecha=1897|publicación=Phil. Mag.|volumen=44|número=266|páginas=55|doi=10.1080/14786449708621028}} {{Cita publicación|título=Doubles and triplets in the spectrum produced by external magnetic forces|apellidos=Zeeman|nombre=P.|fecha=1897|publicación=Phil. Mag.|volumen=44|número=266|páginas=55|doi=10.1080/14786449708621028}} {{Cita publicación|título=Doubles and triplets in the spectrum produced by external magnetic forces|apellidos=Zeeman|nombre=P.|fecha=1897|publicación=Phil. Mag.|volumen=44|número=266|páginas=55|doi=10.1080/14786449708621028}} ( [https://books.google.com/books?id=utXnmtFZ6TUC Google Books] ) |
|||
* {{Cita publicación |
* {{Cita publicación|título=The effect of magnetisation on the nature of light emitted by a substance|apellidos=Zeeman|nombre=P.|fecha=11 February 1897|publicación=Nature|volumen=55|número=1424|páginas=347|bibcode=1897Natur..55..347Z|doi=10.1038/055347a0}} |
||
* {{Cita publicación|url=https://babel.hathitrust.org/cgi/pt?id=uiug.30112109543394;view=1up;seq=19|título=Over doubletten en tripletten in het spectrum, teweeggebracht door uitwendige magnetische krachten|apellidos=Zeeman|nombre=P.|fecha=1897|publicación=Verslagen van de Gewone Vergaderingen der Wis- en Natuurkundige Afdeeling (Koninklijk Akademie van Wetenschappen te Amsterdam) [Reports of the Ordinary Sessions of the Mathematical and Physical Section (Royal Academy of Sciences in Amsterdam)]|volumen=6|páginas=13–18, 99–102, and 260–262|idioma=Dutch|títulotrad=On doublets and triplets in the spectrum, caused by external magnetic forces}} |
|||
* {{Cita publicación|url=https://babel.hathitrust.org/cgi/pt?id=mdp.39015010227844;view=1up;seq=67|título=Doublets and triplets in the spectrum produced by external magnetic forces|apellidos=Zeeman|nombre=P.|fecha=1897|publicación=Philosophical Magazine|volumen=44|número=266|páginas=55–60|serie=5th series|doi=10.1080/14786449708621028}} |
|||
=== Moderno === |
=== Moderno === |
||
* {{ |
* {{Cita libro|apellidos=[[Richard Feynman|Feynman, Richard P.]], [[Robert B. Leighton|Leighton, Robert B.]], [[Matthew Sands|Sands, Matthew]]|título=The Feynman Lectures on Physics|volumen=3|editorial=[[Addison-Wesley]]|fecha=1965|isbn=0-201-02115-3}} |
||
* {{ |
* {{Cita publicación|título=Alfred Landé and the anomalous Zeeman Effect, 1919-1921|apellidos=Forman|nombre=Paul|fecha=1970|publicación=Historical Studies in the Physical Sciences|volumen=2|páginas=153–261|doi=10.2307/27757307}} |
||
* {{ |
* {{Cita libro|nombre=David J.|apellidos=Griffiths|título=Introduction to Quantum Mechanics|edición=2nd|editorial=[[Prentice Hall]]|fecha=2004|isbn=0-13-805326-X|url=https://archive.org/details/introductiontoel00grif_0}} |
||
* {{ |
* {{Cita libro|apellidos=Liboff, Richard L.|enlaceautor=Liboff, Richard L.|título=Introductory Quantum Mechanics|editorial=[[Addison-Wesley]]|fecha=2002|isbn=0-8053-8714-5}} |
||
* {{ |
* {{Cita libro|apellidos=Sobelman, Igor I.|enlaceautor=Sobelman, Igor I.|título=Theory of Atomic Spectra|editorial=Alpha Science|fecha=2006|isbn=1-84265-203-6}} |
||
* {{ |
* {{Cita libro|apellidos=Foot, C. J.|enlaceautor=Foot, C. J.|título=Atomic Physics|fecha=2005|isbn=0-19-850696-1}} |
||
== Enlaces externos == |
|||
* [https://www.holmarc.com/zeeman_effect_apparatus.php Fabricante de aparatos de efecto Zeeman] |
|||
{{Control de autoridades}} |
|||
[[Categoría:Espectroscopia]] |
[[Categoría:Espectroscopia]] |
||
[[Categoría:Wikipedia:Páginas con traducciones sin revisar]] |
|||
Revisión del 14:28 22 feb 2021
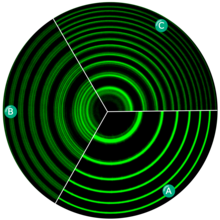
El efecto Zeeman, que lleva el nombre del físico neerlandés Pieter Zeeman, es el efecto de la división de una línea espectral en varios componentes en presencia de un campo magnético estático. Es análogo al efecto Stark, la división de una línea espectral en varios componentes en presencia de un campo eléctrico. También similar al efecto Stark, las transiciones entre diferentes componentes tienen, en general, diferentes intensidades, estando algunas totalmente prohibidas (en la aproximación dipolar), según se rige por las reglas de selección.
Dado que la distancia entre los subniveles de Zeeman es una función de la intensidad del campo magnético, este efecto se puede utilizar para medir la intensidad del campo magnético, por ejemplo, el del Sol y otras estrellas o en plasmas de laboratorio. El efecto Zeeman es muy importante en aplicaciones como la espectroscopia de resonancia magnética nuclear, la espectroscopia de resonancia de espín electrónico, la formación de imágenes por resonancia magnética (MRI) y la espectroscopia de Mössbauer. También se puede utilizar para mejorar la precisión en la espectroscopia de absorción atómica. Una teoría sobre el sentido magnético de las aves asume que una proteína en la retina cambia debido al efecto Zeeman. [1]
Cuando las líneas espectrales son líneas de absorción, el efecto se denomina efecto Zeeman inverso.
Nomenclatura
Históricamente, se distingue entre el efecto Zeeman normal y anómalo (descubierto por Thomas Preston en Dublín, Irlanda [2] ). El efecto anómalo aparece en las transiciones en las que el spin neto de los electrones no es cero. Se le llamó "anómalo" porque el espín del electrón aún no se había descubierto, por lo que no había una buena explicación en el momento en que Zeeman observó el efecto.
A mayor intensidad de campo magnético, el efecto deja de ser lineal. A una fuerza de campo aún mayor, cuando la fuerza del campo externo es comparable a la fuerza del campo interno del átomo, el acoplamiento de electrones se altera y las líneas espectrales se reorganizan. Esto se llama efecto Paschen-Back.
En la literatura científica moderna, estos términos se utilizan raramente, con una tendencia a utilizar solo "efecto Zeeman".
Presentación teórica
El hamiltoniano total de un átomo en un campo magnético es
donde es el hamiltoniano imperturbable del átomo, y es la perturbación debida al campo magnético:
donde es el momento magnético del átomo. El momento magnético consta de las partes electrónicas y nucleares; sin embargo, este último es muchos órdenes de magnitud más pequeño y se pasará por alto aquí. Por lo tanto,
donde es el magnetón de Bohr, es el momento angular electrónico total, y es el factor g de Landé. Un enfoque más preciso es tener en cuenta que el operador del momento magnético de un electrón es una suma de las contribuciones del momento angular orbital y el momento angular de giro , con cada uno multiplicado por la proporción giromagnética apropiada:
donde y (este último se llama relación giromagnética anómala; la desviación del valor de 2 se debe a los efectos de la electrodinámica cuántica). En el caso del acoplamiento LS, se pueden sumar todos los electrones del átomo:
donde y son el momento orbital total y el spin del átomo, y el promedio se realiza sobre un estado con un valor dado del momento angular total.
Si el término de interacción es pequeño (menos que la estructura fina), puede tratarse como una perturbación; este es el efecto Zeeman propiamente dicho. En el efecto Paschen-Back, que se describe a continuación, excede el acoplamiento LS significativamente (pero aún es pequeño en comparación con ). En campos magnéticos ultrafuertes, la interacción del campo magnético puede exceder , en cuyo caso el átomo ya no puede existir en su significado normal, y en su lugar se habla de niveles de Landau. Hay casos intermedios que son más complejos que estos casos límite.
Campo débil (efecto Zeeman)
Si la interacción espín-órbita domina sobre el efecto del campo magnético externo, y no se conservan por separado, solo el momento angular total es. Se puede pensar que los vectores de momento angular orbital y de espín precesan alrededor del vector de momento angular total (fijo) . El vector de giro (tiempo-) "promediado" es entonces la proyección del giro en la dirección de :
y para el vector orbital (tiempo -) "promediado":
Por lo tanto,
Usando y cuadrando ambos lados, obtenemos
y: usando y cuadrando ambos lados, obtenemos
Combinando todo y tomando , obtenemos la energía potencial magnética del átomo en el campo magnético externo aplicado,
donde la cantidad entre corchetes es el factor g Landé gJ del átomo ( y ) y es la componente z del momento angular total. Por un solo electrón por encima de las capas llenas y , el factor g de Landé se puede simplificar en:
Tomando para ser la perturbación, la corrección de Zeeman a la energía es
Ejemplo: transición Lyman-alfa en hidrógeno
La transición Lyman-alfa en hidrógeno en presencia de la interacción espín-órbita implica las transiciones
- y
En presencia de un campo magnético externo, el efecto Zeeman de campo débil divide los niveles 1S1/2 y 2P1/2 en 2 estados cada uno () y el nivel 2P3/2 en 4 estados (). Los factores g de Landé para los tres niveles son:
- por (j = 1/2, l = 0)
- por (j = 1/2, l = 1)
- por (j = 3/2, l = 1).
Tenga en cuenta en particular que el tamaño de la división de energía es diferente para los diferentes orbitales, porque los valores de gJ son diferentes. A la izquierda, se muestra una fina estructura dividida. Esta división ocurre incluso en ausencia de un campo magnético, ya que se debe al acoplamiento espín-órbita. Representado a la derecha es la división adicional de Zeeman, que ocurre en presencia de campos magnéticos.
| Estado inicial
( )
|
Estado final
( )
|
Perturbación energética |
|---|---|---|
Campo fuerte (efecto Paschen-Back)
El efecto Paschen-Back es la división de los niveles de energía atómica en presencia de un fuerte campo magnético. Esto ocurre cuando un campo magnético externo es lo suficientemente fuerte como para interrumpir el acoplamiento entre orbitales () y girar () momentos angulares. Este efecto es el límite de campo fuerte del efecto Zeeman. Cuando , los dos efectos son equivalentes. El efecto lleva el nombre de los físicos alemanes Friedrich Paschen y Ernst E. A. Back. [3]
Cuando la perturbación del campo magnético excede significativamente la interacción espín-órbita, se puede asumir con seguridad . Esto permite que los valores esperados de y para ser fácilmente evaluado por un estado . Las energías son simplemente
Lo anterior puede interpretarse como implicando que el acoplamiento LS está completamente roto por el campo externo. Sin embargo y siguen siendo números cuánticos "buenos". Junto con las reglas de selección para una transición de dipolo eléctrico, es decir, esto permite ignorar por completo el grado de libertad de giro. Como resultado, solo tres líneas espectrales serán visibles, correspondientes a la regla de selección. La división es independiente de las energías no perturbadas y las configuraciones electrónicas de los niveles considerados. En general (si ), estos tres componentes son en realidad grupos de varias transiciones cada uno, debido al acoplamiento de espín-órbita residual.
En general, ahora se debe agregar el acoplamiento de espín-órbita y las correcciones relativistas (que son del mismo orden, conocidas como "estructura fina") como una perturbación a estos niveles "imperturbables". La teoría de perturbación de primer orden con estas correcciones de estructura fina produce la siguiente fórmula para el átomo de hidrógeno en el límite de Paschen – Back: [4]
| Estado inicial
( )
|
Perturbación energética inicial | Estado final
( )
|
|---|---|---|
Campo intermedio para j = 1/2
En la aproximación del dipolo magnético, el hamiltoniano que incluye las interacciones hiperfina y de Zeeman es
donde es la división hiperfina (en Hz) en el campo magnético aplicado cero, y son el magnetón de Bohr y el magnetón nuclear respectivamente, y son los operadores de momento angular de electrones y nucleares y es el factor g de Landé:
- .
En el caso de campos magnéticos débiles, la interacción Zeeman puede tratarse como una perturbación del base. En el régimen de campo alto, el campo magnético se vuelve tan fuerte que dominará el efecto Zeeman, y uno debe usar una base más completa de o solo , ya que y será constante dentro de un nivel dado.
Para obtener una imagen completa, incluidas las intensidades de campo intermedias, debemos considerar los estados propios que son superposiciones de y estados base. Para , el hamiltoniano se puede resolver analíticamente, dando como resultado la fórmula Breit-Rabi. En particular, la interacción cuadrupolo eléctrico es cero para (), por lo que esta fórmula es bastante precisa.
Ahora utilizamos operadores de escalera mecánica cuántica, que se definen para un operador de momento angular general como
Estos operadores de escalera tienen la propiedad
siempre y cuando se encuentra en el rango (de lo contrario, devuelven cero). Usando operadores de escalera y podemos reescribir el hamiltoniano como
Ahora podemos ver que en todo momento, la proyección del momento angular total se conservará. Esto es porque ambos y dejar estados con definidas y sin cambios, mientras y o bien aumentar y disminuir o viceversa, por lo que la suma siempre no se ve afectada. Además, dado que solo hay dos valores posibles de las cuales son . Por lo tanto, para cada valor de solo hay dos estados posibles, y podemos definirlos como base:
Este par de estados es un sistema mecánico cuántico de dos niveles. Ahora podemos determinar los elementos de la matriz del hamiltoniano:
Resolviendo los valores propios de esta matriz, (como se puede hacer a mano o más fácilmente, con un sistema de álgebra por computadora) llegamos a los cambios de energía:
donde es la división (en unidades de Hz) entre dos subniveles hiperfinos en ausencia de campo magnético , se conoce como el 'parámetro de intensidad de campo' (Nota: para la expresión debajo de la raíz cuadrada es un cuadrado exacto, por lo que el último término debe reemplazarse por ). Esta ecuación se conoce como fórmula Breit-Rabi y es útil para sistemas con un electrón de valencia en un () nivel. [5] [6]
Tenga en cuenta que el índice en debe considerarse no como momento angular total del átomo, sino como momento angular total asintótico. Es igual al momento angular total solo si de lo contrario, los vectores propios correspondientes a diferentes valores propios del hamiltoniano son las superposiciones de estados con diferentes pero igual (las únicas excepciones son ).
Aplicaciones
Astrofísica

George Ellery Hale fue el primero en notar el efecto Zeeman en los espectros solares, lo que indica la existencia de fuertes campos magnéticos en las manchas solares. Estos campos pueden ser bastante altos, del orden de 0,1 tesla o más. Hoy en día, el efecto Zeeman se utiliza para producir magnetogramas que muestran la variación del campo magnético del sol.
Refrigeración por láser
El efecto Zeeman se utiliza en muchas aplicaciones de enfriamiento láser, como una trampa magnetoóptica y el Zeeman más lento.
Acoplamiento de espín y movimientos orbitales mediado por la energía de Zeeman
La interacción spin-órbita en los cristales generalmente se atribuye al acoplamiento de matrices de Pauli al impulso de los electrones que existe incluso en ausencia de campo magnético . Sin embargo, bajo las condiciones del efecto Zeeman, cuando , se puede lograr una interacción similar acoplando a la coordenada del electrón a través de la espacialmente no homogénea Zeeman Hamiltoniana
- ,
donde es un factor g tensorial de Landé y o , o ambos, dependen de la coordenada del electrón . Semejante -dependiente Zeeman Hamiltoniano parejas de espín de electrones al operador que representa el movimiento orbital del electrón. Campo no homogéneo puede ser un campo suave de fuentes externas o un campo magnético microscópico de oscilación rápida en antiferromagnetos. [7] Acoplamiento spin-órbita a través de un campo macroscópicamente no homogéneo de nanoimanes se utiliza para la operación eléctrica de espines de electrones en puntos cuánticos a través de la resonancia de espines dipolares eléctricos, [8] y la conducción de espines mediante un campo eléctrico debido a También se ha demostrado. [9]
Véase también
- Efecto Kerr magneto-óptico
- Efecto Voigt
- Efecto Faraday
- Efecto algodón-mouton
- Espectroscopía de polarización
- Energía Zeeman
- Efecto Stark
- Turno de cordero
- La configuración electrónica dice en la subcapa p (l = 1), hay 3 niveles de energía ml = -1,0,1, pero solo vemos dos p1/2 y p3/2, para la subcapa s (l = 0), solo hay 1 nivel de energía (ml = 0), pero aquí tenemos 2. l correspondiente a estructura fina, ml correspondiente a estructura hiperfina.
Referencias
- ↑ Thalau, Peter; Ritz, Thorsten; Burda, Hynek; Wegner, Regina E.; Wiltschko, Roswitha (18 April 2006). «The magnetic compass mechanisms of birds and rodents are based on different physical principles». Journal of the Royal Society Interface 3 (9): 583-587. PMC 1664646. PMID 16849254. doi:10.1098/rsif.2006.0130.
- ↑ Preston, Thomas (1898). «Radiation phenomena in a strong magnetic field». The Scientific Transactions of the Royal Dublin Society. 2nd series 6: 385-342.
- ↑ Paschen, F.; Back, E. (1921). «Liniengruppen magnetisch vervollständigt» [Line groups magnetically completed [i.e., completely resolved]]. Physica (en german) 1: 261-273. Available at: Leiden University (Netherlands)
- ↑ Griffiths, David J. (2004). Introduction to Quantum Mechanics (2nd edición). Prentice Hall. p. 247. ISBN 0-13-111892-7. OCLC 40251748.
- ↑ Woodgate, Gordon Kemble (1980). Elementary Atomic Structure (2nd edición). Oxford, England: Oxford University Press. pp. 193-194.
- ↑ First appeared in: Breit, G.; Rabi, I.I. (1931). «Measurement of nuclear spin». Physical Review 38 (11): 2082-2083. Bibcode:1931PhRv...38.2082B. doi:10.1103/PhysRev.38.2082.2.
- ↑ S. I. Pekar and E. I. Rashba, Combined resonance in crystals in inhomogeneous magnetic fields, Sov. Phys. - JETP 20, 1295 (1965) http://www.jetp.ac.ru/cgi-bin/dn/e_020_05_1295.pdf
- ↑ Y. Tokura, W. G. van der Wiel, T. Obata, and S. Tarucha, Coherent single electron spin control in a slanting Zeeman field, Phys. Rev. Lett. 96, 047202 (2006)
- ↑ Salis G, Kato Y, Ensslin K, Driscoll DC, Gossard AC, Awschalom DD (2001). «Electrical control of spin coherence in semiconductor nanostructures». Nature 414 (6864): 619-622. PMID 11740554. doi:10.1038/414619a.
Histórico
- Condon, E. U.; G. H. Shortley (1935). The Theory of Atomic Spectra. Cambridge University Press. ISBN 0-521-09209-4. (Chapter 16 provides a comprehensive treatment, as of 1935.)
- Zeeman, P. (1896). «Over de invloed eener magnetisatie op den aard van het door een stof uitgezonden licht» [On the influence of magnetism on the nature of the light emitted by a substance]. Verslagen van de Gewone Vergaderingen der Wis- en Natuurkundige Afdeeling (Koninklijk Akademie van Wetenschappen te Amsterdam) [Reports of the Ordinary Sessions of the Mathematical and Physical Section (Royal Academy of Sciences in Amsterdam)] (en dutch) 5: 181-184 and 242-248.
- Zeeman, P. (1897). «On the influence of magnetism on the nature of the light emitted by a substance». Philosophical Magazine. 5th series 43 (262): 226-239. doi:10.1080/14786449708620985.
- Zeeman, P. (11 February 1897). «The effect of magnetisation on the nature of light emitted by a substance». Nature 55 (1424): 347. Bibcode:1897Natur..55..347Z. doi:10.1038/055347a0.
- Zeeman, P. (1897). «Over doubletten en tripletten in het spectrum, teweeggebracht door uitwendige magnetische krachten» [On doublets and triplets in the spectrum, caused by external magnetic forces]. Verslagen van de Gewone Vergaderingen der Wis- en Natuurkundige Afdeeling (Koninklijk Akademie van Wetenschappen te Amsterdam) [Reports of the Ordinary Sessions of the Mathematical and Physical Section (Royal Academy of Sciences in Amsterdam)] (en dutch) 6: 13-18, 99-102, and 260-262.
- Zeeman, P. (1897). «Doublets and triplets in the spectrum produced by external magnetic forces». Philosophical Magazine. 5th series 44 (266): 55-60. doi:10.1080/14786449708621028.
Moderno
- Feynman, Richard P., Leighton, Robert B., Sands, Matthew (1965). The Feynman Lectures on Physics 3. Addison-Wesley. ISBN 0-201-02115-3.
- Forman, Paul (1970). «Alfred Landé and the anomalous Zeeman Effect, 1919-1921». Historical Studies in the Physical Sciences 2: 153-261. doi:10.2307/27757307.
- Griffiths, David J. (2004). Introduction to Quantum Mechanics (2nd edición). Prentice Hall. ISBN 0-13-805326-X.
- Liboff, Richard L. (2002). Introductory Quantum Mechanics. Addison-Wesley. ISBN 0-8053-8714-5.
- Sobelman, Igor I. (2006). Theory of Atomic Spectra. Alpha Science. ISBN 1-84265-203-6.
- Foot, C. J. (2005). Atomic Physics. ISBN 0-19-850696-1.

























![{\displaystyle {\vec {S}}\cdot {\vec {J}}={\frac {1}{2}}(J^{2}+S^{2}-L^{2})={\frac {\hbar ^{2}}{2}}[j(j+1)-l(l+1)+s(s+1)],}](https://wikimedia.org/api/rest_v1/media/math/render/svg/26e9f5a54c934ff91a0ee2e1e0711656fc8a5110)

![{\displaystyle {\vec {L}}\cdot {\vec {J}}={\frac {1}{2}}(J^{2}-S^{2}+L^{2})={\frac {\hbar ^{2}}{2}}[j(j+1)+l(l+1)-s(s+1)].}](https://wikimedia.org/api/rest_v1/media/math/render/svg/394b91804fd17c811c0003f1d0ea096d640f39b7)

![{\displaystyle {\begin{aligned}V_{\rm {M}}&=\mu _{\rm {B}}Bm_{j}\left[g_{L}{\frac {j(j+1)+l(l+1)-s(s+1)}{2j(j+1)}}+g_{S}{\frac {j(j+1)-l(l+1)+s(s+1)}{2j(j+1)}}\right]\\&=\mu _{\rm {B}}Bm_{j}\left[1+(g_{S}-1){\frac {j(j+1)-l(l+1)+s(s+1)}{2j(j+1)}}\right],\\&=\mu _{\rm {B}}Bm_{j}g_{j}\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/213add165a96705cd8e71d5cae67f97afa873ced)































![{\displaystyle [H_{0},S]=0}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c381cfc71af43948523f8c7d1a9fc9d2c8246665)










![{\displaystyle E_{z+fs}=E_{z}+{\frac {m_{e}c^{2}\alpha ^{4}}{2n^{3}}}\left\{{\frac {3}{4n}}-\left[{\frac {l(l+1)-m_{l}m_{s}}{l(l+1/2)(l+1)}}\right]\right\}.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ba7927da53bd8a30b0213965a2a7cad81d83e9c5)






































































