Diferencia entre revisiones de «Número racional»

← Ir a diferencia anterior Ir a siguiente diferencia →

Contenido eliminado Contenido añadido

En renglón

Revisión del 00:06 15 sep 2009

En sentido amplio, se llaman números racionales a todo número que puede representarse como el cociente de dos enteros con denominador distinto de cero (una fracción común). El término «racional» alude a «ración» o «parte de un todo», y no al pensamiento o actitud racional.

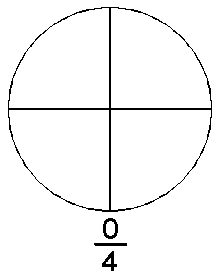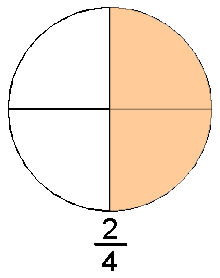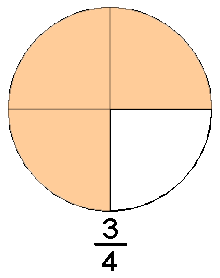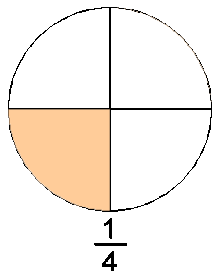
Representación gráfica de las fracciones cuyo divisor es 4.

En sentido estricto, número racional es el conjunto de todas las fracciones equivalentes a una dada; de todas ellas, se toma como representante canónico del dicho número racional a la fracción irreducible, la de términos más sencillos.

Definimos un número racional como un decimal finito o infinito periódico (por ejemplo, el número decimal finito 0,75 es la representación decimal del número racional 3/4. El número decimal infinito periódico 0,333... es la representación decimal del número racional 1/3). El número racional permite resolver ecuaciones del tipo ax = b, cuando a y b son números enteros (con «a» distinto de cero).

El conjunto de los números racionales se denota por $\mathbb {Q}$ , que significa «cociente» (Quotient en varios idiomas europeos). Este conjunto de números incluye a los números enteros y es un subconjunto de los números reales. Las fracciones equivalentes entre sí –número racional– son una clase de equivalencia, resultado de la aplicación de una relación de equivalencia al conjunto de números fraccionarios.

Los números racionales cumplen la propiedad arquimediana o de densidad, esto es, para cualquier pareja de números racionales existe otro número racional situado entre ellos, propiedad que no estaba presente en los números enteros, por lo que los números racionales son densos en la recta de los números reales.

{\begin{array}{ll}\mathbb {C} &{\mbox{Complejos}}{\begin{cases}\mathbb {R} &{\mbox{Reales}}{\begin{cases}\mathbb {Q} &{\mbox{Racionales}}{\begin{cases}\mathbb {Z} &{\mbox{Enteros}}{\begin{cases}\mathbb {N} &{\mbox{Naturales}}\\&{\mbox{Cero}}\\&{\mbox{Enteros negativos}}\end{cases}}\\&{\mbox{Fraccionarios}}\end{cases}}\\&{\mbox{Irracionales}}\end{cases}}\\&{\mbox{Imaginarios}}\end{cases}}\end{array}}

Historia

En el Antiguo Egipto ya se calculaba utilizando fracciones unitarias (aquellas cuyos denominadores son enteros positivos, como: ¹/₂, ¹/₃, ¹/₄). Cualquier fracción que escribimos con un numerador no unitario, los egipcios la escribían como suma de fracciones unitarias distintas, de ahí que las sumas de fracciones unitarias se conozcan como fracción egipcia. Además, se puede demostrar que cualquier número racional positivo se puede escribir como fracción egipcia.

El jeroglífico de una boca abierta (

) denotaba la barra de fracción (/), y un jeroglífico numérico escrito debajo de la "boca abierta", denotaba el denominador de la fracción.

Los babilónicos utilizaban fracciones cuyo denominador era una potencia de 60, mientras que los egipcios usaron, sobre todo, las fracciones con numerador igual a 1. En la escritura, la fracción la expresaban con un óvalo, que significaba parte o partido, y debajo, o al lado, ponían el denominador; el numerador no se ponía por ser siempre 1.

Los griegos y romanos usaron también las fracciones unitarias, cuya utilización persistió hasta la época medieval.

En el siglo XIII Leonardo de Pisa, mejor conocido como Fibonacci, introdujo en Europa la barra horizontal para separar numerador y denominador en las fracciones.

Construcción de los números racionales

Consideremos las parejas de números enteros $\left(a,b\right)$ donde $b\neq 0$ .
${\frac {a}{b}}$ denota a $\left(a,b\right)$ . A $a$ se le llama numerador y a $b$ se le llama denominador
Al conjunto de estos números se le denota por $\mathbb {Q}$ . Es decir $\mathbb {Q} =\left\{{\frac {p}{q}}\mid p\in \mathbb {Z} ,q\in \mathbb {Z} ,q\neq 0\right\}$

Definición de suma y multiplicación en Q

Se define a la suma ${\frac {a}{b}}+{\frac {c}{d}}={\frac {ad+bc}{bd}}$
Se define a la multiplicación ${\frac {a}{b}}\times {\frac {c}{d}}={\frac {ac}{bd}}$

Relaciones de equivalencia y orden en Q

Se define la equivalencia ${\frac {a}{b}}={\frac {c}{d}}$ cuando $ad=bc$
Los racionales positivos son todos los ${\frac {a}{b}}$ tales que $ab>0$
Los racionales negativos son todos los ${\frac {a}{b}}$ tales que $ab<0$
Se define el orden ${\frac {a}{b}}>{\frac {c}{d}}$ cuando $ad-bc>0$

Notación

Los números de tipo ${\frac {-a}{b}}$ son denotados por $-{\frac {a}{b}}$
Las sumas de tipo ${\frac {a}{b}}+{\frac {-c}{d}}$ son denotadas por ${\frac {a}{b}}-{\frac {c}{d}}$
${\frac {a}{b}}\left({\frac {c}{d}}\right)$ denota a ${\frac {a}{b}}\times {\frac {c}{d}}$
Todo número ${\frac {p}{1}}$ se denota simplemente por $p$ .

Propiedades de los números racionales

El conjunto de los números racionales con la suma y multiplicación definida de esta manera forman un Cuerpo.

Propiedades de la suma y multiplicación

La suma en Q es conmutativa, esto es: ${\frac {a}{b}}+{\frac {c}{d}}={\frac {c}{d}}+{\frac {a}{b}}$
La suma en Q es asociativa, esto es: ${\frac {a}{b}}+\left({\frac {c}{d}}+{\frac {p}{q}}\right)=\left({\frac {a}{b}}+{\frac {c}{d}}\right)+{\frac {p}{q}}=\left({\frac {a}{b}}+{\frac {p}{q}}\right)+{\frac {c}{d}}$
La multiplicación en Q es asociativa, esto es: ${\frac {a}{b}}\times \left({\frac {c}{d}}\times {\frac {p}{q}}\right)=\left({\frac {a}{b}}\times {\frac {c}{d}}\right)\times {\frac {p}{q}}$
La multiplicación se distribuye en la suma, esto es ${\frac {a}{b}}\times \left({\frac {c}{d}}+{\frac {p}{q}}\right)=\left({\frac {a}{b}}\times {\frac {c}{d}}\right)+\left({\frac {a}{b}}\times {\frac {p}{q}}\right)$

Existencia de neutros e inversos

Para cualquier racional ${\frac {a}{b}}$ se cumple que ${\frac {a}{b}}+{\frac {0}{1}}={\frac {a}{b}}$ entonces ${\frac {0}{1}}$ es el neutro aditivo de los racionales y se le denota por $0$ .
Para cualquier racional ${\frac {a}{b}}$ se cumple que ${\frac {a}{b}}\times {\frac {1}{1}}={\frac {a}{b}}$ entonces ${\frac {1}{1}}$ es el neutro multiplicativo de los racionales y se le denota por $1$ .
Cada número racional ${\frac {a}{b}}$ tiene un inverso aditivo ${\frac {-a}{b}}$ tal que ${\frac {a}{b}}+{\frac {-a}{b}}=0$
Cada número racional ${\frac {a}{b}}$ con excepción de $0$ tiene un inverso multiplicativo ${\frac {b}{a}}$ tal que ${\frac {a}{b}}\times {\frac {b}{a}}=1$

Equivalencias notables en Q

${\frac {ca}{cb}}={\frac {a}{b}}$ si $c\neq 0$ y $b\neq 0$
${\frac {a}{c}}+{\frac {b}{c}}={\frac {a+b}{c}}$
${\frac {-a}{b}}={\frac {a}{-b}}=-{\frac {a}{b}}$
${\frac {0}{a}}={\frac {0}{b}}=0$ , a y b ≠ 0
${\frac {a}{a}}={\frac {b}{b}}=1$ , a y b ≠ 0.

Los números enteros en Q

Si $p$ es un número entero entonces existe el número ${\frac {p}{1}}$ que equivale a $p$ y mantiene todas sus propiedades de entero. Es decir, se define ${\mathcal {I}}_{\mathbb {Q} }:\mathbb {Z\rightarrow \mathbb {Q} } ,\;{\mathcal {I}}_{\mathbb {Q} }\left(p\right)={\frac {p}{1}}$

Otras notaciones de números en Q

Fracciones mixtas

Cada número racional ${\frac {p}{q}}$ se puede expresar de forma única como $u\left(A+{\frac {a}{b}}\right)$ donde

A es un entero no negativo, es decir $A\in \mathbb {Z} ,~A\geq 0$
${\frac {a}{b}}$ es un racional irreducible no negativo menor que uno. Se expresa como $\mathrm {mcd} \left(a,b\right)=1,\quad 0\leq a<b$
$u$ es una unidad. Es decir $u=\pm 1$

La notación es muy sencilla, las reglas son

$A{\frac {a}{b}}$ denota a $A+{\frac {a}{b}}$
$-A{\frac {a}{b}}$ denota a $-A-{\frac {a}{b}}$

Por ejemplo $-25{\frac {5}{7}}=-{\frac {180}{7}}$

El conjunto de los números decimales en Q

Un número decimal es un número racional de la forma ${\frac {a}{10^{n}}}$
$\mathbb {D}$ denota al conjunto de los números de este tipo. Es decir $\mathbb {D} =\left\{{\frac {a}{10^{n}}}\mid {\frac {a}{10^{n}}}\in \mathbb {Q} \right\}$
Expresión decimal de un número decimal: el número $a$ en base $10$ con un punto a $n$ lugares del extremo derecho, por ejemplo ${\frac {178}{10^{2}}}$ se denota como $1.78$

Representación decimal de los números racionales

Los números racionales se caracterizan por tener un desarrollo decimal cuya expresión sólo puede ser de tres tipos:

Exacta: la parte decimal tiene un número finito de cifras. Ejemplo:

{\frac {8}{5}}=1,6

Periódica pura: toda la parte decimal se repite indefinidamente. Ejemplo:

{\begin{array}{rcl}{\cfrac {1}{7}}&=&0,142857142857\dots \\&=&0,{\overline {142857}}\end{array}}

Periódica mixta: no toda la parte decimal se repite. Ejemplo:

{\begin{array}{rcl}{\cfrac {1}{60}}&=&0,01666\dots \\&=&0,01{\overline {6}}\end{array}}

En efecto, al aplicar el algoritmo para dividir un entero por otro, sólo existen un número finito de restos posibles. Siendo la sucesión de restos infinita, aparecerá forzosamente un mismo resto en dos posiciones distintas. A partir de ellas, el cálculo se repite igual. Ejemplo:

{\begin{array}{r}0,1428571\ldots \\7{\overline {)10\;\,\;\,\;\,\;\,\;\,\;\,\;\,\;\,\;\,\;\,}}\\30\;\,\;\,\;\,\;\,\;\,\;\,\;\,\;\,\;\,\\20\;\,\;\,\;\,\;\,\;\,\;\,\;\,\;\,\\60\;\,\;\,\;\,\;\,\;\,\;\,\;\,\\40\;\,\;\,\;\,\;\,\;\,\;\,\\50\;\,\;\,\;\,\;\,\;\,\\10\;\,\;\,\;\,\;\,\\\vdots \;\,\;\,\;\,\;\,\end{array}}

Recíprocamente, todo número con un desarrollo decimal puede expresarse en fracción de la siguiente manera:

Decimales exactos o finitos: Se escribe en el numerador la expresión decimal sin la coma, y en el denominador un uno seguido de tantos ceros como cifras decimales. Ejemplo: $34,65={\frac {3465}{100}}$
Decimales periódicos puros: La fracción de un número decimal periódico tiene como numerador la diferencia entre el número escrito sin la coma y la parte anterior al periodo; y como denominador, tantos "9" como cifras tiene el periodo. Ejemplo: $15,3434\dots ={\frac {1534-15}{99}}$
Decimales periódicos mixtos: Tendrá como numerador la diferencia entre $a$ y $b$ , donde $a$ es el número escrito sin la coma, y $b$ es el número sin la parte decimal periódica, escrito como número entero. El denominador tendrá tantos "9" como cifras tiene el periodo y otros tantos "0" como cifras decimales no periódicas haya. Ejemplo: Sea el número $12,345676767\dots$ entonces $a=1234567\,$ y $b=12345\,$ , por lo que el número buscado será ${1234567-12345} \over {99000}$ .

Referencias

Cárdenas; Raggi (1990). Álgebra Superior. México D.F. : Trillas. ISBN 968-24-3783-0.

Véase también

@@ Línea 87: / Línea 87: @@
 === Los números enteros en Q ===
-* Si <math>p</math> es un [[número entero]] entonces existe el número <math>\frac{p}{1}</math> que equivale a <math>p</math> y mantiene todas sus propiedades de entero. Es decir, se define <math>\mathcal{I}_{\mathbb{Q}}:\mathbb{Z\rightarrow\mathbb{Q}},\;\mathcal{I}_{\mathbb{Q}}\left(p\right)=\frac{p}{1}</math> y es malaso
+* Si <math>p</math> es un [[número entero]] entonces existe el número <math>\frac{p}{1}</math> que equivale a <math>p</math> y mantiene todas sus propiedades de entero. Es decir, se define <math>\mathcal{I}_{\mathbb{Q}}:\mathbb{Z\rightarrow\mathbb{Q}},\;\mathcal{I}_{\mathbb{Q}}\left(p\right)=\frac{p}{1}</math>
 == Otras notaciones de números en Q ==