Intervalo (matemática)

Un intervalo (del latín intervallum)​ es un subconjunto conexo de la recta real, es decir, un subconjunto que satisface que, para cualesquiera, si, entonces.​ Es un conjunto medible y tiene la misma cardinalidad que la recta real.​

Proposición

Un intervalo $I$ es un subconjunto de $\mathbb {R}$ que verifica la siguiente propiedad:

Si $r$ y $t$ son elementos de $I$ con $r\leq t$, entonces para todo $s$ tal que $r\leq s\leq t$, se cumple que $s\in I$

Notación

Existen dos notaciones principales: en un caso se utilizan corchetes y corchetes invertidos, en el otro corchetes y paréntesis; ambas notaciones están descritas en el estándar internacional ISO 31-11.

Intervalos abiertos

Definición

Dados los números reales a y b que cumplen a<b, se define el conjunto $(a;b)=$ $\{x\in \mathbb {R} :\,a<x<b\}$ llamado intervalo abierto de extremo inferior a y extremo superior b.

En palabras, el intervalo abierto (a;b) es el conjunto de números reales comprendidos entre a y b: este conjunto no contiene a ninguno de los extremos a y b.​ Se le nombra como un tipo de intervalo finito.

Otras notaciones

• $(a;b)\$ o $]a;b[\$ o $<a;b>\$

En la definición de límite ordinario de una función real se considera como dominio un intervalo abierto que contiene al punto de acumulación.

En la topología usual de la recta (o $\mathbb {R}$) se usa un intervalo abierto para definir un conjunto abierto en dicha topología. En la topología usual de $\mathbb {R}$, un intervalo abierto es un conjunto abierto. El intervalo abierto (a; b) es igual a su interior, su frontera es el conjunto {a, b} y su clausura es el intervalo cerrado [a, b]. Su exterior son las semirrectas (-∞; a] y [b; +∞).​ No tiene puntos aislados, mientras que todos sus puntos son puntos de acumulación del mismo intervalo.​

Intervalo cerrado

[[Archivo:Intervalo real 04.svg|derecha|240px] Sí incluye los extremos.

• Que se indica: $I=[a,b]\$

En notación conjuntista:

$I=[a,b]=$ $\{\ x\in I:\quad a\leq x\leq b\}$

Intervalo semiabierto

Incluye únicamente uno de los extremos.

• Con la notación $(a,b]\$ o bien $]a,b]\$ indicamos.

En notación conjuntista:

$I=(a,b]=$ $\{\ x\in I:\quad a<x\leq b\}$

• Y con la notación $[a,b)\$ o bien $[a,b[\$,

En notación conjuntista:

$I=[a,b)=$ $\{\ x\in I:\quad a\leq x<b\}$

Los cuatro tipos de intervalos anteriores se llaman finitos; los expertos asignan como su longitud |b- a|. Son muy útiles en el análisis matemático y en los temas de topología general, para el estudio de diferentes conceptos como clausura, interior, frontera, conexidad, etc.​ Se usan en definición de funciones como la función máximo entero, o la función techo o función piso en matemáticas discretas y para la solución de ecuaciones que conllevan valor absoluto, la función signo, etc.​

Los intervalos finitos tienen un centro de simetría que es (a + b)/2, llamado punto medio, donde los extremos son a y b con a < b. En el caso a=b, no existe punto medio y el intervalo abierto es ∅.​

Intervalos con infinito

Este tipo de intervalos aparece cuando se conoce solo uno de los extremos y el otro es el infinito, es decir, un valor en términos absolutos mayor que cualquier otro, ya sea positivo o negativo. Al no poderse incluir el infinito en el intervalo, estos se consideran siempre abiertos.

Incluye un extremo e infinito por la derecha.

• Con la notación $[a,\infty )\$ indicamos.

En notación conjuntista:

$I=[a,\infty )=$ $\{\ x\in I:\quad a\leq x\}$

Sin incluir el extremo:

• Y con la notación $(a,\infty )$,

$I=(a,\infty )=$ $\{\ x\in I:\quad a<x\}$

Incluye un extremo e infinito por la izquierda.

• Con la notación $(-\infty ,a]\$ indicamos.

En notación conjuntista:

$I=(-\infty ,a]=$ $\{\ x\in I:\quad x\leq a\}$

Sin incluir el extremo:

• Y con la notación $(-\infty ,a)$,

En notación conjuntista:

$I=(-\infty ,a)=$ $\{\ x\in I:\quad x<a\}$

Para todo valor real:

• Y con la notación $(-\infty ,\infty )$,

En notación conjuntista:

$I=(-\infty ,\infty )=$ $\{x\in I:x\in \Re \}=\Re$

Familia de intervalos

• {(1-1/n; 2+1/n) / $n\in \aleph$} es una familia de intervalos abiertos.

• {[1; 2+1/n] / $n\in \aleph$} Es una familia de intervalos cerrados.

Operaciones con intervalos

En notación conjuntista: supongamos el conjunto A:

$A=\{x\in R:\quad x<4\}$

Esto se lee: A es el conjunto de todos los números reales x tal que x es menor que cuatro.

Y el conjunto B:

$B=\{x\in R:\quad 9<x\}$

B es el conjunto de todos los números reales x, tal que 9 es menor que cualquier x .

El conjunto unión de A y B sería:

$A\cup B=\{x\in R:\quad x<4\;\lor \;9<x\}$

O también se puede anotar:

$x\in (-\infty ,4)\cup (9,\infty )$

Un elemento está en la unión de dos o más conjuntos s.s.s. está por lo menos en uno de ellos.

El conjunto intersección de A y B es el vacío:​

$A\cap B=\{x\in R:\quad x<4\;\land \;9<x\}$

porque A y B no tienen puntos en común.

Se nota de la siguiente manera: $A\cap B=\varnothing$

Dados los conjuntos A y C:

$A=\{x\in R:\quad x<4\}$

$C=\{x\in R:\quad -3<x<15\}$

El conjunto unión de A y C es:

$A\cup C=\{x\in R:\quad x<15\}$

El conjunto unión es aquel que toma los valores de cada uno de los conjuntos, entre todos los conjuntos incluidos.

El conjunto intersección de A y C es:

$A\cap C=\{x\in R:\quad -3<x<4\}$

El conjunto intersección es aquel que toma los valores en común entre todos los conjuntos incluidos.

Entorno simétrico

Un entorno simétrico o entorno de centro a y radio r se representa:

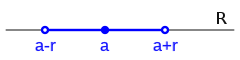
• Con la notación $E(a,r)\$ indicamos.

$I=E(a,r)\Leftrightarrow$ $\{\ x\in I:\quad a-r<x<a+r\}$

Entorno reducido

Un entorno reducido de centro a y radio r se representa:

• Con la notación $E^{\star }(a,r)\$ indicamos.

$I=E^{\star }(a,r)\quad =\{\ x\in I:\quad x\in E(a,r)\;-\;\{a\}\}$

Un entorno reducido de un punto p es un entorno de p, menos {p}. Por ejemplo, el intervalo (−1, 1) = {y $\in \Re$: −1 < y < 1} es un entorno de p = 0 en la recta real, entonces el conjunto (−1, 0) ∪ (0, 1) = (−1, 1) − {0} es un entorno reducido de 0.

Nota

• Si a > b, los intervalos descritos no poseen elementos y denotan al conjunto vacío.
• (a,a), [a,a) y (a,a] denotan también al conjunto vacío.
• [a,a] denota al conjunto unitario {a}, también llamado intervalo degenerado.
• Estas notaciones también se utilizan en otras áreas de las matemáticas; por ejemplo, la notación $(a,b)\$, denota un par ordenado en teoría de conjuntos; las coordenadas de un punto o un vector en geometría analítica y álgebra lineal; un número complejo en álgebra.
• Ambas notaciones admiten el símbolo de infinito ($\infty$) para indicar que no hay cota.

Ejemplos gráficos

[[Archivo:FunEsc Dominio 01.svg|center|border|180x180px|alt=|Gráfica de una función en un intervalo.]] Gráfica de una función en un intervalo.  Transformación lineal de intervalos. Transformación lineal de intervalos.  Transformación lineal de intervalos. Transformación lineal de intervalos.  Recta numérica. Recta numérica.

Clasificación

Se pueden clasificar los intervalos según sus características topológicas (intervalos abiertos, cerrados, semiabiertos) o según sus características métricas (longitud: nula, finita no nula, infinita).

La siguiente tabla resume los 11 casos posibles, con a ≤ b, y x perteneciente al intervalo:

Notación	Intervalo	Longitud	Descripción
$[a,b]\,$	$a\leq x\leq b$	$b-a\,$	Intervalo cerrado de longitud finita.
$[a,b[\ \ \mathrm {\acute {o}} \ \ [a,b)\!$	$a\leq x<b\!$	$b-a\,$	Intervalo semiabierto (cerrado en a, abierto en b).
$]a,b]\ \ \mathrm {\acute {o}} \ \ (a,b]\!$	$a<x\leq b$	$b-a\,$	Intervalo semiabierto (abierto en a, cerrado en b).
$]a,b[\ \ \mathrm {\acute {o}} \ \ (a,b)\!$	$a<x<b\!$	$b-a\,$	Intervalo abierto.
$]-\infty ,b[\ \ \mathrm {\acute {o}} \ \ (-\infty ,b)\!$	$x<b\!$	$\infty$	Intervalo semiabierto.
$]-\infty ,b]\ \ \mathrm {\acute {o}} \ \ (-\infty ,b]\!$	$x\leq b\!$	$\infty$	Intervalo semiabierto.
$[a,\infty [\ \ \mathrm {\acute {o}} \ \ [a,\infty )\!$	$x\geq a\!$	$\infty$	Intervalo semiabierto.
$]a,\infty [\ \ \mathrm {\acute {o}} \ \ (a,\infty )\!$	$x>a\!$	$\infty$	Intervalo semiabierto.
$]\infty ,+\infty [\ \ \mathrm {\acute {o}} \ \ (\infty ,+\infty )\!$	$x\in \mathbb {R} \!$	$\infty$	Conjunto a la vez abierto y cerrado en la topología usual de ℝ.
$\{a\}\!$	$x=a\!$	$0\!$	Intervalo cerrado de longitud nula (intervalo degenerado).
$\{\}=\emptyset \!$	sin elemento	cero	Conjunto vacío Intervalo abierto (a,a).

​

Caracterización

Intervalo cerrado

El número real x está en $I=[a,b]\,$ si sólo si $a\leq x\leq b$. Los puntos a y b son elementos del intervalo cerrado I; a es el ínfimo y b el supremo. El intervalo cerrado es la clausura del intervalo abierto y los semiabiertos con extremos a y b con $a\leq x\leq b$. El intervalo abierto $\ \ (a,b)\!$ es el interior del intervalo cerrado de extremos a y b; y estos puntos son los únicos que están en la frontera del intervalo cerrado $I=[a,b]\,$; este es un conjunto cerrado y compacto con la topología usual de la recta . ​

Propiedades

• La unión de intervalos de $\mathbb {R}$ no siempre es un intervalo (lo será si la intersección es no vacía).
• Los conjuntos conexos de $\mathbb {R}$ son exactamente los intervalos.​
• Los intervalos cerrados sobre una recta se denominan «segmento de recta», son conjuntos cerrados según la topología usual, conexos y compactos.​
• La imagen por una función continua de un intervalo de $\mathbb {R}$ es un intervalo de $\mathbb {R}$. Esta es una formulación del Teorema del valor intermedio.
• Según la topología usual de ℝ, un conjunto abierto es la unión de intervalos abiertos.​

Aritmética de intervalos

Sean I = [a, b] y J = [c, d] con a ≤ x ≤ b, y c ≤ y ≤ d.

Entonces: a + c ≤ x + y ≤ b + d. Lo que justifica que

• I + J = [ a + c, b + d ].

• I - J = [ a - d, b - c ].

• Si se toman a, b, c y d positivos no nulos, I · J = [ ac, bd ] y I / J = [ a/d, b/c ].

Generalización

Un intervalo n-dimensional se define como un subconjunto de $\mathbb {R} ^{n}$, que es el producto cartesiano de n intervalos: $I=I_{1}\times I_{2}\times \cdots \times I_{n}$, uno en cada eje de coordenadas......

Entorno de centro a y radio ε.

En términos topológicos, en el espacio métrico $\mathbb {R}$ usual los intervalos son las bolas abiertas y cerradas. De manera más general, se le llama vecindad o entorno de centro a y radio ε, al conjunto de puntos x cuya distancia a a es menor que ε.

$E(a;\epsilon )=\left\{x\in \mathbb {R} \ :\ |x-a|<\epsilon \right\}$

Véase también

• Desigualdad
• Valor absoluto
• Intervalo unidad
• Partición de un intervalo
• Medida de Lebesgue

Referencias y notas

• Skornyakov, L.A. (2001), «Interval_and_segment&oldid=14087», en Hazewinkel, Michiel, ed., Encyclopaedia of Mathematics (en inglés), Springer, ISBN 978-1556080104 .
• Weisstein, Eric W. «Interval». En Weisstein, Eric W, ed. MathWorld (en inglés). Wolfram Research. 

• Datos: Q185148