Diámetro angular

Diámetro angular (también expresado a veces como «tamaño angular») es la dimensión aparente del diámetro ecuatorial de un cuerpo celeste, expresándola como ángulo y suponiendo al observador en su vértice.[1][2] Para el Sol, la Luna o los planetas la medida del diámetro angular se hace con procedimientos ópticos y micrométricos.[3] En el caso de las estrellas más brillantes, el diámetro angular se mide con procedimientos interferométricos,[4][5] mediante interferómetros. Cuando se trata del ángulo abarcado por el radio ecuatorial, se denomina semidiámetro.
Fórmulas[editar]
El diámetro angular de un objeto circular plano (disco) para un observador situado en una recta perpendicular al plano que contiene al disco y pasa por su centro, puede ser calculado usando la siguiente fórmula matemática:[1]
donde es el diámetro angular buscado, es el diámetro del disco y es la distancia al mismo, ambos expresados en las mismas unidades. El resultado obtenido normalmente se expresa en grados sexagesimales con la parte fraccionaria decimal (por ejemplo, 2,5° corresponde a 2°30′; dos grados y medio en ambos casos).
Cuando se tiene un objeto esférico, a partir de su diámetro , la fórmula resultante es:
donde es el diámetro angular buscado, es el diámetro de la esfera y es la distancia entre el observador y el centro de la esfera; como en el caso anterior, ambos expresados en unidades homogéneas.
La razón de la diferencia entre ambas fórmulas es que cuando se mira a una esfera, los bordes que son los puntos de tangencia de las visuales, están más cerca del observador que el centro de la esfera. Para un uso práctico, la diferencia solo es significativa para objetos esféricos muy próximos al observador, ya que para ángulos pequeños se cumple con notable aproximación que para
- , entonces:[6]
Cuando es mucho más grande que , el ángulo resultante es muy pequeño. En esta situación, el valor del ángulo (expresado en radianes) es muy aproximado al valor de su tangente, por lo que se puede realizar una aproximación con la siguiente fórmula:
(con el águlo también expresado en radianes).[7]
Estimación de diámetros angulares utilizando la mano con el brazo extendido[editar]

Estimaciones de algunos diámetros angulares se pueden obtener mediante la observación de la mano situada perpendicularmente en determinadas posturas con el brazo completamente extendido, como se muestra en la figura adjunta.[8][9][10]
Uso en astronomía[editar]

En astronomía, los tamaños de los objetos en el cielo se dan a menudo en términos de su diámetro angular visto desde la Tierra, en lugar de sus tamaños reales. Dado que estos diámetros angulares son típicamente pequeños, es común representarlos en segundos de arco. Un segundo de arco es 1/3600 de un grado sexagesimal. Sabiendo que medio círculo (180 grados sexagesimales) son radianes, se tiene que un radián equivale a 3600 * 180 / segundos de arco, o lo que es lo mismo, 206.265 segundos de arco. Por lo tanto, el diámetro angular de un objeto con diámetro físico d a una distancia D, expresada en segundos de arco, viene dada por la expresión:[11]
- = (206265) d / D segundos de arco.
Por ejemplo:
- El diámetro angular de la órbita de la Tierra alrededor del Sol, desde una distancia de un parsec, es de 1″ (un segundo de arco).
- El diámetro angular del Sol, desde una distancia de un año luz, es de 0,03″, y el de la Tierra, 0,0003″. El diámetro angular 0,03″ del Sol dado anteriormente, es aproximadamente el mismo que el de una persona a una distancia equivalente al diámetro de la Tierra.[1]
Esta tabla muestra los tamaños angulares de cuerpos celestes notables vistos desde la Tierra:
| Cuerpo celeste | Diámetro angular o tamaño | Tamaño relativo (mínimo y máximo) |
|---|---|---|
| Sol | 31′31″-32′33″ | 30-31 veces el máximo valor para Venus (barra naranja debajo) / 1891-1953″ |
| Luna | 29′20″-34′6″ | 28-32,5 veces el máximo valor para Venus (barra naranja debajo) / 1760-2046″ |
| Nebulosa de la Hélice | 16′-28′ | 15,2-26,6 veces el máximo valor para Venus (barra naranja debajo) / 960-1680″ |
| Espiral en la Nebulosa del Águila | 4′40″ | 4,44 veces el máximo valor para Venus (barra naranja debajo) / 280″ |
| Venus | 9,67″-63,00″ | |
| Júpiter | 29,80″-49,06″ | |
| Saturno | 14,50″-19,92″ | |
| Marte | 3,50″-25,08″ | |
| Mercurio | 4,54″-13,02″ | |
| Urano | 3,31″-4,04″ | |
| Neptuno | 2,17″-2,36″ | |
| Ceres | 0,33″-0,84″ | |
| Asteroide Vesta | 0,20″-0,64″ | |
| Plutón | 0,063″-0,115″ | |
| R Doradus | 0,052″-0,062″ | |
| Betelgeuse | 0,049″-0,060″ | |
| Eris | 0,034″-0,089″ | |
| Alfard | 0,00909″ | |
| Alfa Centauri A | 0,007″ | |
| Canopus | 0,006″ | |
| Sirio | 0,005936″ | |
| Altair | 0,003″ | |
| Deneb | 0,002″ | |
| Próxima Centauri | 0,001″ | |
| Alnitak | 0,0005″ | |
| Una estrella como Alnitak está a una distancia tal que el telescopio espacial Hubble se encuentra en el límite de poder observar su diámetro angular.[12] | 6×10-10″ |
- La tabla muestra que el diámetro angular del Sol, visto desde la Tierra es de aproximadamente 32 minutos de arco (1920 segundos de arco o 0,53 grados), como se ilustra arriba.
- El diámetro angular del Sol es aproximadamente 250.000 veces el de Sirio (Sirio tiene el doble de diámetro que el sol, pero su distancia a la Tierra es 500.000 veces mayor); desde la tierra, el Sol es 1×1010 veces más brillante. De la relación entre sus diámetros angulares, se deduce que Sirio es una estrella aproximadamente 6,25 (=250.000·500.000/2/1×1010) veces más brillante que el Sol por unidad de ángulo sólido.
- El diámetro angular del Sol es también aproximadamente 250.000 veces el de Alfa Centauri A (tiene aproximadamente el mismo diámetro, pero su distancia a la Tierra es de 250.000 veces mayor); desde la Tierra, el Sol es 4×1010 veces más brillante. De la relación entre sus diámetros angulares, se deduce que Alpha Centauri A es una estrella aproximadamente 1,5 (=250.000·250.000/1/4×1010) veces más brillante que el Sol por unidad de ángulo sólido.
- El diámetro angular del Sol es aproximadamente el mismo que el de la Luna: el diámetro del Sol es 400 veces mayor, pero su distancia a la Tierra también lo es. Por otro lado, el Sol es entre 200.000 y 500.000 veces más brillante que la luna llena (las cifras varían en función de factores cambiantes, como la posición relativa entre ambos astros o la luminosidad del sol). Un cuerpo celeste con un diámetro de entre 1,5″ y 4″ y el mismo brillo por unidad de ángulo sólido que el Sol, tendría el mismo brillo que la luna llena (basta dividir el diámetro angular del Sol (1962") por la relación de luminosidad (200.000 a 500.000), y multiplicar por 400 (la relación de distancias a la Tierra entre la Luna y el Sol).
- A pesar de que Plutón es físicamente más grande que Ceres, cuando se ve desde la Tierra (por ejemplo, a través del telescopio espacial Hubble) Ceres tiene un tamaño aparente mucho mayor.
- Mientras tamaños angulares medidos en grados son útiles para grandes zonas del cielo (en la constelación de Orión, por ejemplo, las tres estrellas del cinturón cubren cerca de 4,5 grados de amplitud angular), se necesitan unidades mucho más finas cuando se habla del tamaño angular de galaxias, nebulosas y otros objetos del cielo nocturno.
Orden de magnitud de las unidades angulares[editar]

Como es bien sabido, los grados sexagesimales, se subdividen como sigue:
- 360 grados (°) forman un círculo completo
- 60 minutos de arco (′) son un grado
- 60 segundos de arco (″) son un minuto
Para poner estos valores en perspectiva, baste señalar que tanto el Sol como la luna llena vistos desde la Tierra tienen un diámetro angular de aproximadamente medio grado (o lo que es lo mismo, unos 30 minutos de arco, o 1800 segundos de arco). El movimiento de la luna en el cielo se puede medir en variación angular: 15 grados aproximadamente cada hora, o 15 segundos de arco por segundo. Una línea de una milla de longitud (1,6 km aproximadamente) marcada sobre la superficie de la Luna, se vería desde la Tierra con una amplitud de un segundo de arco.
En astronomía, normalmente es difícil de medir directamente la distancia a un objeto. Pero el objeto puede tener un tamaño físico conocido (siendo similar a un objeto mejor conocido) y un diámetro angular medible. En ese caso, la fórmula del diámetro angular puede ser invertida para calcular la distancia a la Tierra de objetos distantes:
En el espacio no euclidiano, como nuestro universo en expansión, la distancia basada en el diámetro angular es solo una de varias definiciones de distancia, por lo que puede hablarse de diferentes "distancias" a un mismo objeto. (Ver medida de distancias (cosmología)).
Carta de representación de diámetros angulares del Sol, la Luna y los planetas[editar]
Dado que el tamaño aparente se trata de una magnitud angular, es posible establecer una comparación del diámetro angular del Sol, la Luna y los planetas guardando la proporción entre el tamaño al que se representan, y la distancia a la que se observan. Así, para obtener una representation válida de los diámetros angulares de los cuerpos celestes, la imagen debe observarse a una distancia de 103 veces el tamaño máximo de la Luna en la imagen.
Por ejemplo, si el círculo tiene 10 cm de ancho en el monitor, debe observarse a una distancia de 10,3 m.
Objetos no circulares[editar]
Muchos objetos del cielo profundo como galaxias y nebulosas aparecen con formas no circulares, por lo que normalmente se dan dos medidas de diámetro: diámetro mayor y diámetro menor. Por ejemplo, la Pequeña Nube de Magallanes tiene un diámetro aparente visual de 5°20′ x 3°5′.
Defecto de iluminación[editar]
Defecto de iluminación es el ancho angular máximo de la parte no iluminada de un cuerpo celeste visto por un observador dado. Por ejemplo, si un objeto presenta un diámetro de 40 segundos de arco con un 75 por ciento de superficie iluminada, el defecto de iluminación representa 10 segundos de arco (como en el caso de las fases de Venus, por ejemplo).
Ejemplos[editar]
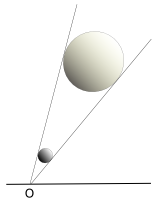
Como se muestra en la figura al margen, dos cuerpos celestes de muy distinto diámetro pueden tener el mismo diámetro angular. Tal es el caso del Sol y la Luna vistos desde la Tierra. El diámetro ecuatorial solar es unas 400 veces mayor que el lunar, pero al ser la distancia Tierra-Sol unas 400 veces mayor que la distancia Tierra-Luna, ambos cuerpos tienen diámetros angulares sensiblemente iguales, en torno a los 30 minutos de arco, y así nuestro satélite puede ocultar completamente al Sol, en algunos casos, produciéndose un eclipse solar total.
Para hacernos una idea de la verdadera magnitud del diámetro angular, imaginemos una moneda de 2 euros puesta a diferentes distancias:
- A unos 1,5 metros el diámetro angular es de 1°
- A casi 90 metros, su diámetro angular vale 1′
- Finalmente, a poco más de 5 kilómetros, el ángulo es de 1″
Véase también[editar]
- Separación angular
- Ángulo sólido
- Distancia del diámetro angular
- Resolución óptica
- Agudeza visual
- Lista de estrellas con imágenes resueltas
Enlaces externos[editar]
- Video sobre el diámetro angular y el seno y coseno
- Tamaños angulares de los satélites de los planetas del sistema solar. Posibilidades de eclipse (Creation Research Society. En inglés. Consultado el 30/10/2015)
Referencias[editar]










