Ángulos adyacentes

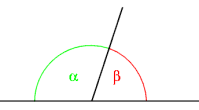
Ángulos adyacentes.

Ángulos adyacentes son aquellos ángulos que tienen el vértice y un lado en común, al tiempo que sus otros dos lados son semirrectas opuestas a veces pueden tener hasta 4 lados, dependiendo de los vértices. De allí resulta que los ángulos adyacentes son a la vez consecutivos y suplementarios, porque juntos equivalen a un ángulo llano (180°), sin poseer ningún punto interior en común.​​​

Otros autores denominan ángulos adyacentes a los ángulos consecutivos.

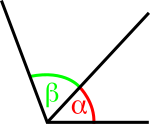
En la literatura del tema es posible también encontrar casos donde se denomina como adyacentes a cualquier par de ángulos que compartan el vértice y un lado, aunque no sean suplementarios (es decir, se llaman adyacentes a los ángulos que en otros textos se denominan consecutivos),​​ quizás debido a la influencia del inglés en donde adjacent angles tiene este significado. Por ello es importante al abordar un texto sobre el tema, tener presente cual es la convención usada. En este artículo se efectúa la distinción, considerando únicamente el caso en que los lados no comunes formen una línea recta, reservando el artículo ángulos consecutivos para la otra acepción.

Propiedades

• Los senos de los ángulos adyacentes son los mismos, por ejemplo:

sen( 120° ) = sen( 60° )

sen( α ) = sen( 180° - α )

sen( α ) = sen( π - α )

• Los cosenos de los ángulos adyacentes son de igual valor absoluto, pero de signo inverso, como muestran los siguientes ejemplos:

cos( 120° ) = - cos( 60° )

cos( α ) = - cos( 180° - α )

cos( α ) = - cos( π - α )

Véase también

Relaciones aritméticas entre ángulos:

• Ángulos congruentes
• Ángulos complementarios
• Ángulos suplementarios
• Ángulos conjugados

Relaciones posicionales entre ángulos:

• Ángulos consecutivos
• Ángulos opuestos por el vértice
• Ángulos interiores y exteriores

Determinados por dos paralelas y una transversal

• Ángulos correspondientes
• Ángulos alternos

Enlaces externos

• Complementary Angles animated demonstration. With interactive applet
• Supplementary Angles animated demonstration. With interactive applet
• Angle definition pages with interactive applets that are also useful in a classroom setting. Math Open Reference

• Datos: Q2750842