Concavidad
En geometría, la concavidad de una curva o de una superficie es la parte que se asemeja a la zona interior de una circunferencia o de una esfera,[1] es decir, que tiene su parte hundida dirigida al observador.[2] Es el concepto complementario al de convexidad.
Ángulos cóncavos
[editar]
|
Sin embargo, la definición de ángulo cóncavo es la siguiente: un ángulo es cóncavo, reflejo o entrante si mide más de 180° y menos de 360° (más de rad y menos de rad). |
Figuras geométricas cóncavas
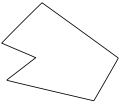
[editar]Un polígono es cóncavo, si al atravesarlo una recta puede cortarlo en tres o más puntos. Posee al menos un ángulo interior cóncavo.
-
Polígono simple, cóncavo, irregular.
-
Polígono convexo, regular (equilátero y equiángulo).
Funciones algebraicas cóncavas
[editar]
Una función es cóncava cuando dados dos puntos cualesquiera, el segmento que los une queda por debajo de la curva. Presenta su concavidad hacia abajo.[3]
La concavidad, como característica del gráfico de una función, se refiere a la condición geométrica de la región situada bajo una curva.
Se dice que una función f(x) es cóncava cuando la región bajo la curva es convexa, en caso de que la función sea dos veces derivable, esta es cóncava si, y solo si, f"(x) < 0.
Una función cóncava, también se llama cóncava hacia abajo, mientras que una función convexa es llamada cóncava hacia arriba.