Teorema de Euler para poliedros

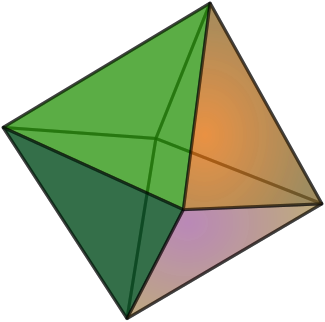
 El conocido cubo con 8 vértices, 12 aristas y 6 caras cumple con el teorema del poliedro euleriano.
El conocido cubo con 8 vértices, 12 aristas y 6 caras cumple con el teorema del poliedro euleriano.El teorema de Euler para poliedros es un teorema matemático de la geometría del espacio, Leonhard Euler en 1750, y publicado en la obra "Elementa doctrinae solidorum" en 1758. El teorema indica la relación entre el número de caras, aristas y vértices de un poliedro convexo sin orificios, ni entrantes.[1] Expresa una constante que no se altera en caso de rotaciones, traslaciones de dichos poliedros. En la proposición también concluye que solo pueden ser cinco los sólidos regulares y establece para ellos varias relaciones:
Detrás de la fórmula está el concepto topológico de la característica de Euler-Poincaré. La fórmula del poliedro de Euler es el caso especial para (tres dimensiones) con descuido implícito de (siempre consideramos un solo cuerpo) entonces resulta un :
- ( según el teorema del poliedro de Euler)
- ( según las características de Euler-Poincaré)
con Número de vértices, Número de aristas, Número de caras y Número de celdas.
En general, es válida (desde que se define así) para los poliedros de la característica (o ), que incluye todos los poliedros convexos sin excepción y muchos poliedros cóncavos "bien comportados", véase la sección validez.[2]
Teorema de los poliedros[editar]
donde:
= Número de caras
= Número de vértices
= Número de aristas
= Número de lados del polígono regular
= Número de aristas que convergen en los vértices
La relación (1) se llama característica de Euler y sigue cumpliéndose para todos los poliedros convexos.
Ejemplo[editar]
Para un cubo se tiene . La característica de Euler es . Cada cara es un cuadrado, por tanto . En cada vértice concurren aristas.
- Los casos más conocidos corresponden a los poliedros regulares: tetraedro, cubo, octaedro, dodecaedro e icosaedro.
Demostración[editar]
Cabe decir que Euler jamás fue capaz de dar una demostración correcta de este resultado, de hecho la que aparece en su "Elementa doctrinae solidorum" era errónea. Anteriormente a 1750 pocos fueron los que se dedicaron a este asunto. René Descartes se había ocupado de escribir el primer tratado sobre poliedros, pero murió antes de poder publicarlo. Tras su muerte, sus trabajos fueron trasladados a Francia, donde después de sufrir algún percance en dicho traslado (parece ser que cayeron a un río y fueron recuperados y secados), llegaron a las manos de Gottfried Wilhelm Leibniz, quien se encargó de transcribir parte de dichos trabajos. Sin embargo dichas transcripciones no vieron la luz hasta después de 1860, casi 80 años después de la muerte de Euler. Fue Augustin Louis Cauchy quien, en 1811, publicó la primera demostración general que se conoce.
Supóngase que se elimina una cara del poliedro. El resto del poliedro puede ser deformado, de manera que se convierta en una figura plana de puntos y curvas cuya frontera corresponda a las aristas de la cara eliminada (basta simplemente con proyectarlo sobre un plano). Puede suponerse, sin pérdida de generalidad por ello, que las aristas deformadas son segmentos de líneas rectas. Al realizar la proyección, a pesar de que las caras pueden presentar una forma distinta, es evidente que el número de vértices, caras y aristas coinciden con los del poliedro de partida (suponiendo que la cara extraída corresponde al exterior de la figura).
A continuación se aplican las siguientes transformaciones que simplifican la figura, pero que no afectan a la característica de Euler :
- Si algún polígono tiene más de tres lados, se dibuja una diagonal. Esto añade una arista y una cara. Se continúa así hasta que todas las caras sean triangulares.
- Se elimina de uno en uno los triángulos con un solo lado en contacto con el exterior. Esto disminuye el número de aristas y caras en una unidad, pero no altera el número de vértices.
- Se elimina de uno en uno todos los triángulos que tienen dos lados en contacto con el exterior de la figura. Esto elimina un vértice, dos aristas y una cara.
Aplicando sucesivamente los pasos 2 y 3, al final queda un único triángulo. Resulta evidente que ahora (contando el exterior), y , cuya característica de Euler es 2.

Validez[editar]
El teorema del poliedro de Euler se aplica a todos los poliedros convexos. La convexidad es una condición demasiado fuerte:
- Empujar un vértice del icosaedro no cambia el número de vértices, aristas o caras, por lo que la convexidad no importa.
- Incluso el hecho de empujar un vértice a través de otra cara no la cambia, siempre y cuando se ignoren las intersecciones y las líneas de intersección que sólo surgen en la geometría.
- Tampoco es necesario un poliedro, ya que las caras curvas y las aristas curvas no influyen mientras el mallado no cambie.
- En topología, a diferencia de la geometría, no existe el concepto de convexidad. El cargo no juega un papel, sólo sus conexiones.
Sin embargo, excluye de forma fiable todos los casos que conducen a una violación del teorema del poliedro de Euler.
Que conduce a las desviaciones:
- Falta de libertad de paso o falta de orientación clara de las zonas.
- El poliedro total no debe consistir espacialmente en dos o más poliedros individuales separados que se toquen sólo en una esquina o en una arista. De lo contrario, aumenta en . En la forma más general como característica de Euler-Poincaré esto no supone un problema, porque al mismo tiempo el número de celdas también aumenta en por lo que se aplica de nuevo lo siguiente .
- La red de vértices y aristas debe estar topológicamente conectada, es decir, debe surgir un grafo común. Otros gráficos aumentan por o se consideran de manera diferente: se aplica por separado para cada gráfico.
- El poliedro no debe contener ningún "agujero" o "asa", es decir, debe tener el género topológico . Cada agujero reduce en (si el poliedro está formado por caras orientables), en caso contrario en .
Si estos errores se equilibran exactamente, se puede volver a cumplir el teorema del poliedro de Euler, por ejemplo, un cubo con un cuboide como agujero perforado (16 vértices, 24 aristas, 10 caras).
-
 El octaedro convexo con 6 vértices, 12 aristas y 8 caras satisface con el teorema del poliedro euleriano.
El octaedro convexo con 6 vértices, 12 aristas y 8 caras satisface con el teorema del poliedro euleriano. -
 El tetrahemiexaedro cóncavo con 6 vértices, 12 aristas, pero sólo 7 caras viola con el teorema del poliedro euleriano. Los 3 cuadrados amarillos interiores se cruzan entre sí y no tienen lados interiores y exteriores más definidos. El cuerpo es homeomorfo a la superficie de Steiner. Ya no se puede representar como un gráfico plano.
El tetrahemiexaedro cóncavo con 6 vértices, 12 aristas, pero sólo 7 caras viola con el teorema del poliedro euleriano. Los 3 cuadrados amarillos interiores se cruzan entre sí y no tienen lados interiores y exteriores más definidos. El cuerpo es homeomorfo a la superficie de Steiner. Ya no se puede representar como un gráfico plano. -
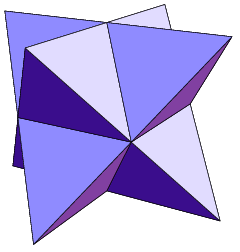
 El tetraedro estrella cóncavo con 14 vértices, 36 aristas y 24 caras vuelve a cumplir con el teorema del poliedro euleriano.
El tetraedro estrella cóncavo con 14 vértices, 36 aristas y 24 caras vuelve a cumplir con el teorema del poliedro euleriano. -
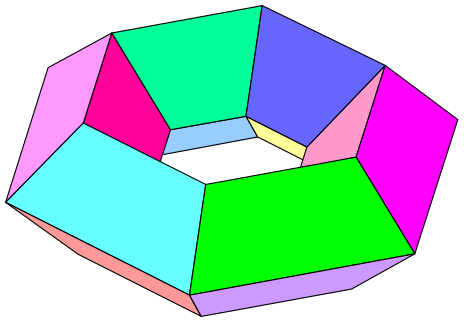
 El poliedro cóncavo de Szilassi con un "agujero" () con 14 vértices, 21 aristas y 7 caras viola con viola el teorema del poliedro euleriano.
El poliedro cóncavo de Szilassi con un "agujero" () con 14 vértices, 21 aristas y 7 caras viola con viola el teorema del poliedro euleriano. -
 Un "poliedro donut" con 30 vértices, 60 aristas y 30 cuadriláteros como caras viola con viola el teorema del poliedro de Euler.
Un "poliedro donut" con 30 vértices, 60 aristas y 30 cuadriláteros como caras viola con viola el teorema del poliedro de Euler. -
 Este poliedro cóncavo tiene 32 vértices, 90 aristas y 60 caras y satisface con el teorema del poliedro euleriano. Sin embargo …
Este poliedro cóncavo tiene 32 vértices, 90 aristas y 60 caras y satisface con el teorema del poliedro euleriano. Sin embargo … -
 … la estrella del dodecaedro, que a primera vista parece igual, como un cuerpo de Kepler-Poinsot sólo tiene 12 vértices (marcados en oro, los otros 20 son sólo intersecciones de las aristas), 30 aristas (que se dividen cada una en tres por las 20 intersecciones) y 12 caras (pentagramas, cada uno de los cuales se descompone en 5 triángulos) y viola con el teorema del poliedro de Euler .
… la estrella del dodecaedro, que a primera vista parece igual, como un cuerpo de Kepler-Poinsot sólo tiene 12 vértices (marcados en oro, los otros 20 son sólo intersecciones de las aristas), 30 aristas (que se dividen cada una en tres por las 20 intersecciones) y 12 caras (pentagramas, cada uno de los cuales se descompone en 5 triángulos) y viola con el teorema del poliedro de Euler .
Diferencia entre el octaedro y el tetrahemihexaedro[editar]
Ambos tienen el mismo número de vértices y aristas. Sin embargo, el modelo de superficie del tetrahemihexaedro ya no representa un gráfico plano sin intersecciones.
- Vemos las 6 vértices y las 12 aristas de ambos sólidos.
- Las caras del octaedro son las 4 caras rojizas y las 4 caras azuladas (una de las cuales es la cara exterior).
- Las caras del tetrahemihexaedro son las 4 caras rojas (correspondientes a las caras rojas del modelo giratorio), así como otras 3 caras compuestas (correspondientes a las caras amarillas del modelo giratorio), que ya no corresponden a zonas simples del gráfico. Para ello, toma uno de los 6 vértices y sigue las cuatro aristas de este vértice hasta los vértices directamente conectados a este vértice. Estos son los 4 vértices de cada uno de los 3 cuadrados, cada uno con las dos orientaciones posibles (las caras ya no tienen un interior y un exterior), que forman las otras 3 caras.
Otros casos[editar]
Pirámide pentagonal[editar]
- Base:1 pentágono simple; caras laterales: 5 triángulos escalenos (en general). Números de caras=6=C.
- Aristas: 5 de la base y 5 de los vértices de la base al vértice de la pirámide. Número de aristas=A=10
- Vértices: 5 en la base y el ápice 1. Número de vértices = V=6
- Se cumple la característica euleriana: C+V=A+2, ya que 6+6=10+2.
Prisma triangular[editar]
- 2 bases: triángulos; tres caras laterales: paralelogramos. Número de caras=C=5
- Aristas: 6 en ambas bases y 3 en caras laterales. Número de aristas=A=9
- Vértices: 3 en cada bas. Número de vértices=V=6
- Se cumple la característica euleriana:C+V=A+2, ya que 5+6=9+2.[3]
Véase también[editar]
Referencias[editar]
- ↑ Una definición: Un poliedro es convexo si el sólido queda por completo de un mismo lado de un plano que contiene a una cara cualquiera. (Geometría superior), de Bruño.
- ↑ Darauf wies zuerst Louis Poinsot 1810 hin.
- ↑ Adaptación del libro Característica euleriana de Yu. Shashkin Editorial Mir, Moscú.
Enlaces externos[editar]
- Weisstein, Eric W. «Polyhedral Formula». En Weisstein, Eric W, ed. MathWorld (en inglés). Wolfram Research.
- Euler, Leonhard (1758). Elementa doctrinae solidorum.