La función f (x ) (en azul) es aproximada por la función lineal (en rojo). En análisis numérico la regla del trapecio es un método de integración , es decir, un método para calcular aproximadamente el valor de una integral definida . La regla se basa en aproximar el valor de la integral de
f
(
x
)
{\displaystyle f(x)}
función lineal , que pasa a través de los puntos
(
a
,
f
(
a
)
)
{\displaystyle (a,f(a))}
(
b
,
f
(
b
)
)
{\displaystyle (b,f(b))}
área del trapecio bajo la gráfica de la función lineal .
Regla del trapecio Simple [ editar ] Para realizar la aproximación por esta regla es necesario usar un polinomio de primer orden, y esta es representada por:
P
1
(
x
)
=
f
(
a
)
+
f
(
b
)
−
f
(
a
)
b
−
a
(
x
−
a
)
{\displaystyle P_{1}(x)=f(a)+{\frac {f(b)-f(a)}{b-a}}(x-a)}
Entonces al sustituir en la integral tenemos lo siguiente:
I
=
∫
a
b
f
(
x
)
d
x
≈
∫
a
b
P
1
(
x
)
d
x
≈
∫
a
b
[
f
(
a
)
+
f
(
b
)
−
f
(
a
)
b
−
a
(
x
−
a
)
]
d
x
{\displaystyle {\begin{aligned}I&=\int _{a}^{b}f(x)dx\approx \int _{a}^{b}P_{1}(x)\,dx\\&\approx \int _{a}^{b}\left[f(a)+{\frac {f(b)-f(a)}{b-a}}(x-a)\right]\,dx\end{aligned}}}
Por último al resolver esa integral nos queda:
∫
a
b
f
(
x
)
d
x
≈
(
b
−
a
)
f
(
a
)
+
f
(
b
)
2
{\displaystyle \int _{a}^{b}f(x)dx\approx (b-a){\frac {f(a)+f(b)}{2}}}
El término de error corresponde a:
E
t
=
−
1
12
f
″
(
ξ
)
(
b
−
a
)
3
{\displaystyle E_{t}=-{\frac {1}{12}}f''(\xi )(b-a)^{3}}
Siendo
ξ
{\displaystyle \xi }
intervalo
[
a
,
b
]
{\displaystyle [a,b]}
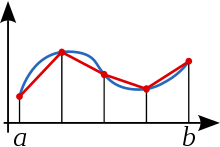
Regla del trapecio compuesta [ editar ] Ilustración de la regla del trapecio compuesta La regla del trapecio compuesta o regla de los trapecios es una forma de aproximar una integral definida utilizando n trapecios. En la formulación de este método se supone que
f
{\displaystyle f}
[
a
,
b
]
{\displaystyle [a,b]}
∫
a
b
f
(
x
)
d
x
{\displaystyle \int _{a}^{b}f(x)\,dx}
f
{\displaystyle f}
O
x
{\displaystyle Ox}
x
=
a
{\displaystyle x=a}
x
=
b
{\displaystyle x=b}
[
a
,
b
]
{\displaystyle [a,b]}
n
{\displaystyle n}
Δ
x
=
(
b
−
a
)
/
n
{\displaystyle \Delta x=(b-a)/n}
Después de realizar todo el proceso matemático se llega a la siguiente fórmula:
∫
a
b
f
(
x
)
d
x
∼
h
2
[
f
(
a
)
+
2
f
(
a
+
h
)
+
2
f
(
a
+
2
h
)
+
.
.
.
+
f
(
b
)
]
{\displaystyle \int _{a}^{b}f(x)\,dx\sim {\frac {h}{2}}[f(a)+2f(a+h)+2f(a+2h)+...+f(b)]}
Donde
h
=
b
−
a
n
{\displaystyle h={\frac {b-a}{n}}}
n
{\displaystyle n}
La expresión anterior también se puede escribir como:
∫
a
b
f
(
x
)
d
x
∼
b
−
a
n
[
f
(
a
)
+
f
(
b
)
2
+
∑
k
=
1
n
−
1
f
(
a
+
k
b
−
a
n
)
]
{\displaystyle \int _{a}^{b}f(x)dx\sim {\frac {b-a}{n}}\left[{\frac {f(a)+f(b)}{2}}+\sum _{k=1}^{n-1}f\left(a+k{\frac {b-a}{n}}\right)\right]}
El error en esta aproximación se corresponde con :
−
(
b
−
a
)
3
12
n
2
f
″
(
ξ
)
{\displaystyle -{\frac {(b-a)^{3}}{12n^{2}}}\,f''(\xi )}
Siendo n el número de subintervalos
∫
0
2
3
x
d
x
{\displaystyle \int _{0}^{2}3x\,dx}
n
=
6
{\displaystyle n=6}
Primero se obtiene
h
{\displaystyle h}
a
{\displaystyle a}
b
{\displaystyle b}
n
=
6
{\displaystyle n=6}
h
=
b
−
a
n
{\displaystyle h={\frac {b-a}{n}}}
=
2
−
0
6
=
1
3
{\displaystyle ={\frac {2-0}{6}}={\frac {1}{3}}}
Y ahora se sustituye en la fórmula
∫
a
b
f
(
x
)
d
x
{\displaystyle \int _{a}^{b}f(x)\,dx}
h
2
[
f
(
a
)
+
2
f
(
a
+
h
)
+
2
f
(
a
+
2
h
)
+
.
.
.
+
f
(
b
)
]
{\displaystyle {\frac {h}{2}}[f(a)+2f(a+h)+2f(a+2h)+...+f(b)]}
y queda:
∫
0
2
3
x
d
x
{\displaystyle \int _{0}^{2}3x\,dx}
1
2
⋅
1
3
[
3
(
0
)
+
2
[
3
(
0
+
1
⋅
1
3
)
]
+
2
[
3
(
0
+
2
⋅
1
3
)
]
+
2
[
3
(
0
+
3
⋅
1
3
)
]
+
2
[
3
(
0
+
4
⋅
1
3
)
]
+
2
[
3
(
0
+
5
⋅
1
3
)
]
+
3
(
2
)
]
=
6
{\displaystyle {\frac {1}{2}}\cdot {\frac {1}{3}}[3(0)+2[3(0+1\cdot {\frac {1}{3}})]+2[3(0+2\cdot {\frac {1}{3}})]+2[3(0+3\cdot {\frac {1}{3}})]+2[3(0+4\cdot {\frac {1}{3}})]+2[3(0+5\cdot {\frac {1}{3}})]+3(2)]=6}
![{\displaystyle {\begin{aligned}I&=\int _{a}^{b}f(x)dx\approx \int _{a}^{b}P_{1}(x)\,dx\\&\approx \int _{a}^{b}\left[f(a)+{\frac {f(b)-f(a)}{b-a}}(x-a)\right]\,dx\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/a4a0e1eb1d1c3de0a21bc7bf51a3fe6a106e5492)
![{\displaystyle [a,b]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9c4b788fc5c637e26ee98b45f89a5c08c85f7935)
![{\displaystyle \int _{a}^{b}f(x)\,dx\sim {\frac {h}{2}}[f(a)+2f(a+h)+2f(a+2h)+...+f(b)]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/2f1b5c6a7245887f1241f8a623edf4c3975c1ec2)
![{\displaystyle \int _{a}^{b}f(x)dx\sim {\frac {b-a}{n}}\left[{\frac {f(a)+f(b)}{2}}+\sum _{k=1}^{n-1}f\left(a+k{\frac {b-a}{n}}\right)\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ed95b3abd58bd3f419658c546afcd7b1fd48ca24)
![{\displaystyle {\frac {h}{2}}[f(a)+2f(a+h)+2f(a+2h)+...+f(b)]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/118092dfd0e9a60f55b8c1a5529fafc8d4651909)
![{\displaystyle {\frac {1}{2}}\cdot {\frac {1}{3}}[3(0)+2[3(0+1\cdot {\frac {1}{3}})]+2[3(0+2\cdot {\frac {1}{3}})]+2[3(0+3\cdot {\frac {1}{3}})]+2[3(0+4\cdot {\frac {1}{3}})]+2[3(0+5\cdot {\frac {1}{3}})]+3(2)]=6}](https://wikimedia.org/api/rest_v1/media/math/render/svg/127b399633f6ba67d620e0cb098adb25bd7058f0)
Wikisource contiene obras originales sobre la Generalización de la fórmula de Simpson. (La regla de los trapecios como caso particular de la generalización de la regla de Simpson)
Datos: Q833293
Multimedia: Trapezium rule / Q833293