Modulación por desplazamiento de fase
La modulación por desplazamiento de fase o PSK (Phase Shift Keying) es una forma de modulación angular que consiste en hacer variar la fase de la portadora entre un número determinado de valores discretos. La diferencia con la modulación de fase convencional (PM) es que mientras en esta la variación de fase es continua, en función de la señal moduladora, en la PSK la señal moduladora es una señal digital y, por tanto, con un número de estados limitado.
Introducción[editar]
La modulación PSK se caracteriza porque la fase de la señal portadora representa cada símbolo de información de la señal moduladora, con un valor angular que el modulador elige entre un conjunto discreto de "n" valores posibles.
Un modulador PSK representa directamente la información mediante el valor absoluto de la fase de la señal modulada, valor que el demodulador obtiene al comparar la fase de esta con la fase de la portadora sin modular.

La señal modulada resultante, responde a la expresión:
Donde:
- =amplitud
- =frecuencia
- =tiempo
- =representa cada uno de los valores posibles de la fase, tantos como estados tenga la señal codificada en banda base multinivel.
Dependiendo del número de posibles fases a tomar, recibe diferentes denominaciones. Dado que lo más común es codificar un número entero de bits por cada símbolo, el número de fases a tomar es una potencia de dos. Así tendremos BPSK con 2 fases (equivalente a PAM), QPSK con 4 fases (equivalente a QAM), 8-PSK con 8 fases y así sucesivamente. A mayor número de posibles fases, mayor es la cantidad de información que se puede transmitir utilizando el mismo ancho de banda, pero mayor es también su sensibilidad frente a ruidos e interferencias.
Las modulaciones BPSK y QPSK, derivadas de la modulación por desplazamiento de fase, son óptimas desde el punto de vista de protección frente a errores. En esencia, la diferencia entre distintos símbolos asociados a cada fase es máxima para la potencia y ancho de banda utilizados. No pasa lo mismo con otras variantes tales como la PSK de 8 niveles (8-PSK), la de 16 (16-PSK) o superiores, para las cuales existen otros esquemas de modulación digital más eficientes.
La gran ventaja de las modulaciones PSK es que la potencia de todos los símbolos es la misma, por lo que se simplifica el diseño de los amplificadores y etapas receptoras lo que significa reducción de costos, dado que la potencia de la fuente es constante.
Existen 2 alternativas de modulación PSK: PSK convencional, donde se tienen en cuenta los desplazamientos de fase, y PSK diferencial (DPSK), en la cual se consideran las diferencias entre un salto de fase y el anterior.
Descripción matemática[editar]
Definiciones[editar]
Para establecer matemáticamente las tasas de error correspondientes a cada modulación, definiremos algunos conceptos:
- = Energía por bit
- = Energía por símbolo = con k bits por símbolo
- = Duración del bit
- = Duración del símbolo
- = Densidad espectral de potencia de ruido(W/Hz)
- = Probabilidad de bit erróneo
- = Probabilidad de símbolo erróneo
Cálculo de tasas de error[editar]
La función se utiliza para calcular la tasa de errores en una modulación. Es la forma normalizada de la función de error gaussiana complementaria:
- .
Velocidad de transmisión[editar]
La velocidad de transmisión de los símbolos en PSK viene dada por la expresión:
Donde:
- : número de niveles de la señal digital.
- : Velocidad de transmisión en bits/segundo.
: Velocidad de transmisión en baudios.
Aplicaciones[editar]
Debido a su mayor simplicidad frente a la modulación QAM, PSK es una modulación ampliamente extendida. El estándar de red LAN inalámbrica, IEEE 802.11b-1999, usa una variedad de diferentes modulaciones PSK, dependiendo de la velocidad de transmisión. A 1Mbps usa DBPSK (BPSK diferencial), a 2Mbps emplea DQPSK y para 5,5Mbps y 11Mbps, usa QPSK pero debe ser usada junto con modulación de código complementario. El estándar IEEE 802.11g-2003, para LANs inalámbricas de alta velocidad, tiene 8 tasas de velocidad de datos: 6, 9, 12, 18, 24, 36, 48 y 54 Mbps. Los modos de 6 y 9 Mbps usan modulación OFDM con subportadoras que son moduladas con BPSK y OFDM con QPSK para 12 y 18Mbps. Los cuatro modos más rápidos usan la modulación OFDM con diversas formas de QAM.
Por su simplicidad, la modulación BPSK es utilizada para transmisores pasivos de bajo coste y es utilizada en estándares RFID como el ISO 14443, que se ha adoptado en pasaportes biométricos o tarjetas de crédito, además de otras muchas aplicaciones. La norma Bluetooth 2.0 usa la modulación π/4-DQPSK para su mínima velocidad de 2 Mbit/s y a la máxima, que es de 3 Mbps usa 8-DPSK cuando el enlace entre dos dispositivos sea robusto. En el Bluetooth 1 se usa la modulación de desplazamiento mínimo gaussiano, un esquema binario, así que cualquiera de las opciones de modulación en la versión 2 dará lugar a una mayor velocidad de datos.
Una tecnología similar, IEEE 802.15.4 (el estándar inalámbrico utilizado por ZigBee) también se basa en PSK. La norma IEEE 802.15.4 permite el uso de dos bandas de frecuencias: 868 a 915 MHz usando BPSK y a 2,4 GHz utilizando OQPSK. Un notable ausente de estos esquemas diversos es la modulación 8-PSK. Esto se debe a que su tasa de error es cercana a la de 16-QAM, pero su velocidad de datos es de solo tres cuartas partes de esta última. Así 8-PSK se omite a menudo de las normas y los esquemas tienden a "saltar" de QPSK a 16-QAM, aunque es posible usar la modulación 8-QAM, pero es difícil de implementar.
Tipos de modulaciones PSK[editar]
Las modulaciones PSK pueden dividirse en dos grandes grupos: las modulaciones PSK convencionales, en las que la información se codifica en el valor del salto de fase, y las modulaciones PSK diferenciales, en las que el valor del salto de fase respecto al del salto anterior, es el que contiene la información.
BPSK (PSK Binario)[editar]

Este esquema es la modulación de desplazamiento de fase de 2 símbolos. También se la conoce como 2-PSK o PRK (Phase Reversal Keying). Es el más sencillo de todos, puesto que solo emplea 2 símbolos, con 1 bit de información cada uno. Es también la que presenta mayor inmunidad al ruido, puesto que la diferencia entre símbolos es máxima (180°). Dichos símbolos suelen tener un valor de salto de fase de 0° para el 1 y 180° para el 0, como se muestra en un diagrama de constelación. En cambio, su velocidad de transmisión es la más baja de las modulaciones de fase.
En presencia de un desplazamiento de fase, introducido por el canal de comunicaciones, el demodulador de BPSK es incapaz de determinar el símbolo correcto. Debido a esto, el flujo de datos es codificado en forma diferencial antes de la modulación. BPSK es funcionalmente equivalente a la modulación 2-QAM.
Implementación[editar]
La descripción matemática de una señal modulada BPSK es la siguiente:
Esta expresión proporciona dos fases: 0° y 180° (π radianes). En la forma específica, los datos binarios se transmiten a menudo con las siguientes señales:
donde:
- : frecuencia de la onda portadora.
- : señal de salida para el "0" lógico.
- : señal de salida para el "1" lógico.
Por lo tanto, el espacio de señal que es el cociente puede ser representado por la función base:
donde 1 es representado por y 0 por . Esta asignación es, por supuesto, arbitraria.
Tasa de errores[editar]
La tasa de bits erróneos de BPSK es baja, debido a su máxima separación entre saltos de fase. Esta tasa con ruido blanco gaussiano y aditivo se puede calcular como:
donde es la función de error complementaria. Ya que en el esquema digital BPSK solo hay un bit por símbolo, esta es también la tasa de error de símbolo.
QPSK (Quadrature Phase-Shift Keying)[editar]

Este esquema de modulación es conocido también como Quaternary PSK (PSK Cuaternaria), Quadriphase PSK (PSK Cuadrafásica) o 4-QAM, pese a las diferencias existentes entre QAM y QPSK. Esta modulación digital es representada en el diagrama de constelación por cuatro puntos equidistantes del origen de coordenadas. Con cuatro fases, QPSK puede codificar dos bits por cada símbolo. La asignación de bits a cada símbolo suele hacerse mediante el código Gray, que consiste en que, entre dos símbolos adyacentes, los símbolos solo se diferencian en 1 bit, con lo que se logra minimizar la tasa de bits erróneos.
El análisis matemático muestra que un sistema QPSK puede usarse tanto para duplicar la tasa de datos, en comparación con otro BPSK mientras se mantiene el ancho de banda de la señal o para mantener la tasas de datos de BPSK sin dividir a la mitad el ancho de banda. En este último caso, la tasa de errores de bit (BER) es exactamente igual para ambas modulaciones, lo que puede originar confusiones al describirlas y considerarlas.
Respecto a un ancho de banda predeterminado, la ventaja de QPSK sobre BPSK está que con el primero se transmite el doble de la velocidad de datos en un ancho de banda determinado en comparación con BPSK, usando la misma tasa de error. Como contraparte, los transmisores y receptores QPSK son más complicados que los de BPSK, aunque con las modernas tecnologías electrónicas, el costo es muy moderado.
Como ocurre con BPSK, hay problemas de ambigüedad de fase en el extremo receptor, y a menudo se utiliza QPSK codificado en forma diferencial en la práctica.
Implementación[editar]
La implementación de QPSK es más general que la de BPSK y también indica la aplicación de modulación PSK de orden superior. Escribiendo la ecuación que representa al símbolo n-ésimo, , en el diagrama de constelación en términos de las ondas portadoras en cuadratura se obtiene:
lo cual proporciona las fases de 45° (π/4 rad), 135° (3π/4 rad), 225° (5π/4 rad) y 315° (7π/4 rad).
Las ondas portadoras son representadas con las funciones base siguientes:
siendo el componente "en-fase" (eje I) de la señal y el componente en cuadratura. Por tanto, cada uno de los puntos del diagrama de constelación se representa, sustituyendo a "n" por los cuatro valores que son aceptados, mediante las coordenadas:
Comparando las funciones de base obtenidas con las de BPSK, se muestra claramente que QPSK se puede ver como dos señales BPSK independientes. Hay que tener en cuenta que para los puntos de espacio de señal para BPSK no es necesario dividir el símbolo (bit) de energía a través de los dos portadores en el esquema mostrado en el diagrama de constelación BPSK.
Los sistemas QPSK se pueden implementar en diversas formas. Las siguientes gráficas muestran los principales componentes del transmisor y del receptor:


Tasa de error de bit[editar]
Aunque QPSK puede ser vista como una modulación cuaternaria, es más fácil de verla como dos portadoras en cuadratura moduladas de forma independiente. Con esta interpretación, los bits pares (o impares) se utilizan para modular la componente en fase de la portadora, mientras que los demás bits se utilizan para modular la componente en cuadratura de fase de la portadora. BPSK se utiliza en ambas portadoras y pueden ser independientemente demoduladas.
Como resultado, la probabilidad de error de bit para QPSK es la misma que para BPSK:
Sin embargo, con el fin de lograr la misma probabilidad de error de bit que tiene BPSK, QPSK utiliza el doble de la potencia, ya que dos bits se transmiten simultáneamente.
La tasa de error de símbolo está dada por:
| . |
Si la relación de señal a ruido es alta, como ocurre en los sistemas prácticos QPSK, la probabilidad de error de símbolo se puede aproximar a:
QPSK en el dominio temporal[editar]
Para comprender el funcionamiento de QPSK en el dominio temporal, es necesario analizar lo que ocurre cuando las portadoras en cuadratura son moduladas con un flujo de datos que contiene todas las señales posibles. En el diagrama anexo, se pueden observar las señales I y Q que se obtienen a la salida de cada modulador y la señal total a la salida del sumador lineal.
Variantes de QPSK[editar]
OQPSK (QPSK con corrimiento)[editar]
Es una variante de QPSK, llamada QPSK con corrimiento,,[1] QPSK compensada,[2] QPSK desplazada y, a veces, SQPSK (sigla de Staggered quadrature phase-shift keying, Modulación por desplazamiento de fase en cuadratura escalonada) en la cual las formas de onda I y Q se desplazan entre sí en la mitad de un tiempo de bit.[2] Para lograr esto, se introduce en el canal en cuadratura Q un dispositivo que introduzca el retardo ya mencionado.

El tomar cuatro valores de la fase (dos bits) a la vez para construir un símbolo QPSK puede permitir que la fase de la señal salte hasta 180° a la vez. Cuando la señal pasa por un filtro de paso bajo (como es típico en un transmisor), estos desplazamientos de fase dan como resultado fluctuaciones de gran amplitud, algo indeseable en los sistemas de comunicación. Mediante la compensación o desviación de la sincronización de los bits "en-fase" (I) y "en cuadratura" (Q) por un periodo de bit, o la mitad de un período de símbolo, los componentes en fase y en cuadratura no cambiarán nunca al mismo tiempo. En el diagrama de constelación respectivo, se puede ver que esto limitará el desplazamiento de fase a no más de 90° a la vez. Esto proporciona fluctuaciones de amplitud mucho menores que en la QPSK tradicional y se prefiere a veces en la práctica.
El diagrama temporal bajo estas líneas muestra la diferencia en el comportamiento de la fase entre la QPSK tradicional y la compensada. Aquí puede observarse que en el diagrama superior la fase puede cambiar hasta 180° a la vez, mientras que los cambios de fase en OQPSK nunca son mayores a 90°.

La representación en el eje del tiempo de una señal típica en OQPSK es mostrada en el diagrama de abajo. Obsérvese el desfase por un período de medio símbolo entre las señales I y Q. Los cambios abruptos de fase ocurren aproximadamente dos veces, al igual que en QPSK pero son más pequeños.

Considerar que para la imagen que muestra la señal modulada en el dominio del tiempo la referencia es una función seno positiva con fase de 0°.
π/4–QPSK[editar]

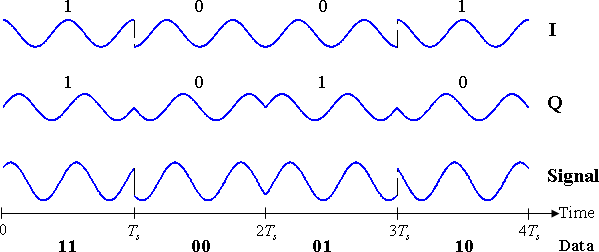
Esta variante de QPSK utiliza dos constelaciones idénticas que son giradas en 45° o π/4 (de ahí su nombre) una con respecto a la otra. Por lo general, cualquiera de los símbolos pares o impares se utilizan para seleccionar los puntos de una de las constelaciones y los otros símbolos seleccionan puntos de la otra. Esto también reduce los desfases hasta un máximo de 135°.
Una propiedad que este esquema de modulación posee, es que si la señal modulada se representa en el plano complejo, esta no pasa por el origen. Esto reduce el rango dinámico de las fluctuaciones en la señal, lo que es deseable cuando se producen las señales de comunicaciones. Por otra parte, este tipo de modulación se presta a una demodulación fácil y ha sido adoptado para su uso en, por ejemplo, la técnica TDMA de redes de telefonía celular.
Abajo se muestra el diagrama temporal para este esquema de modulación. La construcción de la señal es la misma que en la QPSK tradicional. Los símbolos sucesivos son tomados de las dos constelaciones que forman este esquema. Así, el primer símbolo (marcado como 1 1) es tomado de la constelación coloreada de azul y el segundo símbolo (0 0) proviene de la constelación en verde. Puede notarse que las magnitudes de las ondas I y Q cambian mientras se hacen cambios de símbolos entre constelaciones, pero la magnitud de la señal total permanece constante.

SOQPSK (Shaped OQPSK)[editar]
El esquema de modulación digital SOQPSK (Shaped Offset QPSK, que puede traducirse como QPSK de desplazamiento continuo) es una modulación altamente eficiente en cuanto al uso de ancho de banda, ya que, al igual que en OQPSK, las señales en los canales I y Q son desplazadas por la mitad de un tiempo de símbolo, por lo que no existen desplazamientos de fase de 180° y se limita el uso del ancho de banda. La SOQPSK lleva más allá la eficiencia en el uso del ancho de banda ya que las transiciones de fase son continuas (shaped, como se denomina en la jerga técnica en idioma inglés) en lugar de ser instantáneas como en los demás esquemas.[3]
La señal en SOQPSK tiene la forma de un modulación de fase continua y se define mediante la siguiente fórmula:[4]
donde:
es la función que transporta los cambios de fase y
es la fase inicial.
A su vez, es definida mediante la sumatoria:
con:
En estas últimas ecuaciones, es el índice de modulación es el pulso de fase y denota la frecuencia instantánea de una función de pulso y los números son los símbolos transmitidos que toman los valores de +1, 0 y -1. Por tanto, esta es una modulación continua de fase de tipo ternario.
Para generar una señal SOQPSK se usa un sistema que se presenta en el diagrama de bloques, en el cual el flujo de datos de tipo NRZ (no-retorno a cero) es introducido a un precodificador que genera una señal ternaria y los pulsos que se generan son "suavizados" para ahorrar ancho de banda y luego pasados por un integrador, para luego generar las señales respectivas en los canales I y Q del modulador digital.
FQPSK (Feher-patented QPSK)[editar]
La modulación digital FQPSK (Feher-patented QPSK, que puede traducirse como "QPSK patentado por Feher"), es un esquema de QPSK patentado por el científico estadounidense Kamilo Feher[5][6] que engloba la combinación de envolvente constante y estrechamiento del ancho de banda basándose en la modulación OQPSK.[4] El flujo de datos de entrada sin retorno a cero (NRZ) es dividido en dos canales de datos I y Q mediante un convertidor serie a paralelo. La señal del canal Q es retrasada en una cantidad de medio tiempo de símbolo. Las señales obtenidas son rectangulares y los filtros IJF (Interference and Jitter Free, Libre de Interferencia y Jitter, en idioma español) se encargan de "suavizar" los pulsos para disminuir el ancho de banda. Las señales ya procesadas son introducidas al bloque de correlator cruzado, el cual se encarga de reducir la fluctuación de la señal de 3dB a 0dB, de modo que se pueda generar una señal con envolvente constante o casi constante, pero ampliando ligeramente su ancho de banda. Las señales de salida del correlator, I(t) y Q(t) mediante dos moduladores de producto, modulan una misma señal portadora con diferencia de fase de 90°, en un montaje similar a de las modulaciones QAM y QPSK.
El receptor para este esquema en su forma óptima es complejo. La señal recibida, como en otras modulaciones digitales, es dividida en dos y se dirige a dos moduladores de producto que usan la señal portadora recuperada con un desfase de 90°. La salida de cada modulador es procesada para obtener las señales y a partir de las cuales, se obtienen las señales I y Q originales.
DPQPSK[editar]
Es la sigla de Dual-polarization quadrature phase shift keying (que puede traducirse como Modulación por desplazamiento de fase en cuadratura de polarización dual), esquema que implica la multiplexación de polarización de dos señales diferentes QPSK, lo que duplica la eficiencia espectral. Esta es una alternativa efectiva en costo, a la utilización de 16-PSK en lugar de QPSK para duplicar la eficiencia espectral.
PSK de Orden Superior[editar]
Cualquier número de fases puede ser utilizado para construir una constelación de modulación PSK, pero 8-PSK, es por lo general la constelación de orden más alto PSK implementada. Con más de 8 fases, la tasa de error es demasiado alta y existen mejores modulaciones disponibles, aunque más complejas, tales como la modulación de amplitud en cuadratura (QAM). Aunque cualquier número de fases puede ser utilizado, el hecho de que la constelación normalmente deba tratar con datos binarios significa que el número de símbolos es normalmente una potencia de 2, lo cual permite un número igual de bits por símbolo.
Tasa de error de bit[editar]
En general para una modulación PSK de orden M, también llamada M-PSK, no existe una expresión sencilla para el cálculo probabilidad de error de símbolo si M>4. Solo puede derivarse de la siguiente ecuación:
donde:
- ,
- ,
- ,
siendo estas tres últimas, variables aleatorias conjuntas gausianas.

La probabilidad puede ser calculada, en forma aproximada, para valores altos de M y de mediante la expresión:
- .
La probabilidad de error de bit para M-PSK solo se puede determinar exactamente una vez que se conoce la asignación de bits. Sin embargo, cuando se utiliza la codificación Gray, el error más probable de un símbolo al siguiente produce solo un único bit de error y por ello:
- .
El uso de codificación Gray permite aproximar el cálculo de la distancia de Lee de los errores, así como la distancia de Hamming de los errores en el flujo de bits decodificado, que es más fácil de implementar en hardware.
En el gráfico anexo a la izquierda, son comparadas las tasas de error de bit de las modulaciones BPSK, QPSK, 8-PSK y 16-PSK. Se observa que las modulaciones de orden superior presentan mayores tasas de errores; sin embargo, a cambio ofrecen una mayor velocidad de datos en bruto.
Los límites en las tasas de error de los diversos esquemas de modulación digital se pueden calcular con la aplicación de la desigualdad de Boole a la constelación de la señal.
PSK diferencial (DPSK)[editar]
Véase también[editar]
 Wikiversidad alberga proyectos de aprendizaje sobre Modulación por desplazamiento de fase.
Wikiversidad alberga proyectos de aprendizaje sobre Modulación por desplazamiento de fase.- Modulación por desplazamiento diferencial de fase (DPSK)
- Clavisaje[7]
Referencias[editar]
- ↑ Couch, Leon (2008). «Capítulo 5: Sistemas modulados de AM, FM y digitales». En Luis Miguel Cruz Castillo, ed. Sistemas de comunicación digitales y analógicos. Pearson Educación. p. 358. ISBN 978-970-26-1216-2.
- ↑ a b Tomasi, Wayne (2008). «Capítulo 12: Comunicaciones digitales». En Guillermo Trujano Mendoza, ed. Sistemas de Comunicaciones Electrónicas. México: Pearson Educación. p. 490. ISBN 970-26-0316-1.
- ↑ Perrins, Erik; Robert Schober, Michael Rice y Marvin Simon (junio de 2006). Shaped-Offset QPSK with Multiple-Bit Differential Detection [QPSK de compensación continua con detección diferencial de varios bits.] (pdf) (en inglés) 3. pp. 1212 - 1218. ISBN 1-4244-0355-3. doi:10.1109/ICC.2006.254913. Resumen divulgativo.
- ↑ a b Yongzhao, Lin; Xuewen, Liu (2006). «Two Classes of Modulation Schemes for Deep Space Communications». China Communications (en inglés) 4 (6): 9. Archivado desde el original el 8 de noviembre de 2007. Consultado el 14 de agosto de 2015.
- ↑ Santana, Carmen (11 de abril de 2012). «El rey del mundo de las patentes». La Provincia. Consultado el 20 de diciembre de 2012.
- ↑ Simon, Marvin K; Divsalar, Dariush (19 de febrero de 2008). Reduced complexity coding system using iterative decoding (en inglés). Consultado el 25 de enero de 2013.
- ↑ Keying (telecommunications) (en inglés)

![{\displaystyle A_{p}\cdot \cos[2\pi ft+\theta ]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/eaa7b2418875f14d4399704cc1207f4a5bc9ea35)






























































