Mapa autoorganizado
Un mapa autoorganizado (en inglés: self-organizing map, SOM) o un mapa autoorganizado de características (self-organizing feature map, SOFM) es un tipo de red neuronal artificial (ANN por sus siglas en inglés), que es entrenada usando aprendizaje no supervisado para producir una representación discreta del espacio de las muestras de entrada, llamado mapa.
Introducción[editar]
Los mapas autoorganizados son diferentes de otras redes neuronales artificiales, en el sentido que estos usan una función de vecindad para preservar las propiedades topológicas del espacio de entrada.
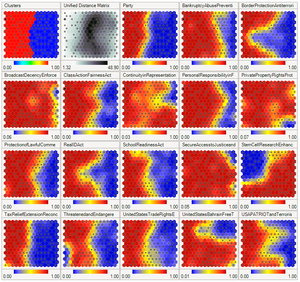
Los SOMs son útiles para visualizar vistas de baja dimensión de datos de alta dimensión, semejante a un escalado multidimensional. El modelo fue descrito por primera vez como una red neuronal artificial por el profesor finlandés Teuvo Kohonen, debido a lo cual en ocasiones son llamadas redes o mapas de Kohonen.[1][2]
Al igual que la mayoría de las redes neuronales artificiales, los SOMs operan en dos modos: entrenamiento y mapeo. En el entrenamiento construye el mapa usando ejemplos entrenantes, mientras que en el mapeo clasifica una nueva entrada.
Un mapa autoorganizado consiste en componentes llamadas nodos o neuronas. Asociado con cada neurona hay un vector de pesos, de la misma dimensión de los vectores de entrada, y una posición en el mapa. La configuración usual de las neuronas es un espacio regular de dos dimensiones, en una rejilla hexagonal o rectangular. Los mapas autoorganizados describen un mapeo de un espacio de mayor dimensión a uno de menor dimensión. El procedimiento para ubicar un vector del espacio de los datos en el mapa es encontrar la neurona con el vector de pesos más cercano (menor distancia métrica) al vector del espacio de los datos.
Mientras que es típico considerar este tipo de estructura de la red de la misma familia que las redes con retro-alimentación, donde los nodos son visualizados como si estuvieran adheridos, este tipo de arquitectura es diferente en configuración y motivación.
Existen extensiones útiles que incluyen el uso de rejillas toroidales donde los ejes opuestos son conectados y usan un gran número de neuronas. Se ha demostrado que mientras los SOMs con un pequeño número de neuronas tienen un comportamiento similar a las K-medias, los grandes mapas autoorganizados reconfiguran los datos de forma fundamentalmente topológica en carácter.
Es también común el uso de matrices U.[3] El valor de la matriz U de una neurona en particular es la distancia promedio entre la neurona y sus vecinos más cercanos.[4] Por ejemplo en una rejilla cuadrada se deben considerar cercanos 4 u 8 neuronas, según las vecindades de Von Neumann y Moore respectivamente.
En grandes SOMs aparecen propiedades emergentes. En mapas compuestos por cientos de neuronas es posible desarrollar operaciones de agrupamiento en el propio mapa.[5]
Algoritmo de aprendizaje[editar]
El objetivo del aprendizaje en los mapas autoorganizados es provocar que diferentes partes de la red respondan similarmente a ciertos patrones de la entrada. Esto es parcialmente motivado por el manejo en partes separadas de la corteza cerebral del cerebro humano de la información sensorial, como la visual y la auditiva.[6]

Los pesos de las neuronas son inicializados con un pequeño valor aleatorio o muestreados uniformemente de un subespacio generado por los dos mayores vectores propios. Con la segunda alternativa el aprendizaje es mucho más rápido puesto que los pesos iniciales ya dan una buena aproximación de los pesos reales.[7]
La red debe ser alimentada con un gran número de ejemplos entrenantes que representen, tan bien como sea posible, la naturaleza de los vectores esperados durante el mapeo. Los ejemplos usualmente son administrados varias veces de forma iterativa.
El entrenamiento utiliza aprendizaje competitivo. Cuando un ejemplo entrenante es presentado a la red, su distancia euclidiana a todos los vectores de pesos es calculada. La neurona cuyo vector de pesos es más similar a la entrada es llamada unidad de mejor correspondencia (BMU por sus siglas en inglés). Los pesos del BMU y las neuronas cercanas al mismo en la cuadrícula del SOM son ajustados hacia el vector de entrada. La magnitud de los cambios se decrementan con el tiempo y con la distancia desde el BMU. La fórmula para actualizar una neurona con vector de peso es
donde es el índice del paso, es el índice dentro del conjunto entrenante, es el índice de BMU para es el coeficiente monótonamente decreciente de aprendizaje y es el vector de entrada; se asume que visite todas las neuronas para cada valor de y .[8] Dependiendo de la implementación, t puede barrer el conjunto de entrenamiento sistemáticamente, puede ser escogido aleatoriamente del conjunto de entrenamiento (bootstrap sampling), o mediante otro método de muestreo (como jackknife).
La función de vecindad depende de la distancia de cuadrículas entre la BMU (neurona ) y la neurona . De forma simple se le da el valor 1 a todas las neuronas suficientemente cerca a BMU y 0 a las otras, pero es más común elegir una función gaussiana. Independientemente de la forma funcional, la función de vecindad se contrae con el tiempo.[6] Al inicio, cuando la vecindad es completa, la autoorganización tiene lugar a escala global. Cuando la vecindad ha sido ajustada a solo unas cuantas neuronas, los pesos irán convergiendo a estimaciones locales. En algunas implementaciones, el coeficiente de aprendizaje, , y la función de vecindad, , decrecen de manera constante con el incremento de , en otras (en particular aquellas donde explora rápidamente el conjunto de entrenamiento) el decrecimiento ocurre más lentamente.
Este proceso es repetido para cada vector de entrada un número de ciclos, , usualmente grande. La red va asociando las neuronas de salida con grupos o patrones en el conjunto de entrenamiento. Si estos patrones son nombrados, los nombres pueden ser anexados con las neuronas asociadas en la red de entrenamiento.
Durante el mapeo, solo existirá una neurona ganadora, la neurona cuyo vector de pesos se encuentre más cerca del vector de entrada. Esto puede ser determinado de forma simple calculando la distancia euclidiana entre el vector de entrada y los vectores de pesos.
Mientras que la representación de los datos de entrada como vectores ha sido enfatizado en este artículo, se debe notar que cualquier clase de objeto puede ser representado digitalmente, definiendo una medida de distancia apropiada y las operaciones necesarias para que sea posible el entrenamiento usado para la construcción del mapa autoorganizado. Esto incluye matrices, funciones continuas, e incluso otros mapas autoorganizados.
Variables[editar]
Las variables necesitadas en los mapas autoorganizados son resumidas como:
- es la iteración actual.
- es la cantidad total de iteraciones.
- es el índice del vector de entrada en el conjunto de datos de entrada .
- es un vector de entrada de índice del conjunto de datos de entrada .
- es el índice de una neurona en el mapa.
- es el vector de pesos de la neurona v.
- es el índice del BMU en el mapa.
- es la función de vecindad.
- es un restrictor de aprendizaje debido al progreso de las iteraciones.
Algoritmo[editar]
- Hacer un mapa de neuronas con vectores de pesos aleatorios.
- Tomar un vector de entrada .
- Iterar por cada neurona del mapa.
- Calcular la distancia entre el vector de entrada y los vectores de pesos de las neuronas del mapa.
- Mantener la neurona que ha tenido la menor distancia, esta neurona será el BMU.
- Actualizar las neuronas en la vecindad del BMU.
- Iterar por cada neurona del mapa.
- Incrementar s y volver al paso 2, mientras .
Interpretación[editar]
Hay dos formas de interpretar los mapas autoorganizados. Debido a que en la fase de entrenamiento los pesos de toda la vecindad son movidos en la misma dirección, elementos similares tienden a excitar neuronas adyacentes. Por tanto, SOMs forman un mapa semántico donde muestras similares son mapeadas juntas, y las diferentes aparte. Esto puede ser visualizado por una matriz U del SOM.[3][4]
La otra forma es pensar en los pesos de las neuronas como punteros al espacio de entrada. Estos forman una aproximación discreta de la distribución de las muestras de entrenamiento. Se producen más punteros a regiones de alta concentración de muestras de entrenamiento y menos donde las muestras son más escasas.
Los mapas autoorganizados se consideran una generalización no linear del análisis de componentes principales (PCA por sus siglas en inglés).[9] Esto ha sido mostrado usando datos geofísicos artificiales y reales, donde los SOMs ha tenido gran ventaja sobre los métodos convencionales de extracción de características como son las funciones ortogonales empíricas y el PCA.
Originalmente, los SOMs no fueron formulados como una solución a problemas de optimización. No obstante, ha habido varios intentos por modificar la definición de los SOMs para dar solución a estos problemas con resultados similares.[10]
Alternativas[editar]
- El mapa topográfico generativo (GTM por sus siglas en inglés) es una alternativa potencial al SOM. En el sentido que un GMT requiere explícitamente un suave y continuo mapeo desde el espacio de entrada al espacio del mapa, preserva la topológia. Sin embargo, en sentido práctico, esta medida de preservación topológica es deficiente.[11]
- El mapa de tiempo adaptativo autoorganizado (TASOM por sus siglas en inglés) es una extensión de los SOMs. Los TASOMs emplean tasas de aprendizaje adaptativo y funciones de vecindad. También incluyen un parámetro de escalado para hacer la red invariante en escalado, rotación y traslación del espacio de entrada. Los TASOMs y sus variantes han sido usadas en varias aplicaciones, dentro de las que se incluye el agrupamiento adaptativo, los umbrales multiniveles, aproximación del espacio de entrada, y modelación de contornos activos.[12]
- El mapa autoorganizado crecientes (GSOM por sus siglas en inglés) es una variante creciente del SOM. El GSOM fue desarrollado para manejar el problema de identificar un mapa de tamaño adecuado en los SOMs. Comienza con un mínimo número de neuronas (usualmente cuatro), y crecen nuevos nodos en los bordes basados en una heurística.
Referencias[editar]
- ↑ Kohonen, Teuvo; Honkela, Timo (2007). «Kohonen Network». Scholarpedia.
- ↑ Kohonen, Teuvo (1982). «Self-Organized Formation of Topologically Correct Feature Maps». Biological Cybernetics 43 (1): 59-69.
- ↑ a b Ultsch, Alfred; Siemon, H. Peter (1990). «Kohonen's Self Organizing Feature Maps for Exploratory Data Analysis». En Widrow, Bernard; Angeniol, Bernard, eds. Proceedings of the International Neural Network Conference (INNC-90), Paris, France, July 9–13, 1990 1. Dordrecht, Netherlands: Kluwer. pp. 305-308. ISBN 978-0-7923-0831-7. Archivado desde el original el 13 de junio de 2013. Consultado el 21 de diciembre de 2012.
- ↑ a b Ultsch, Alfred (2003); U*-Matrix: A tool to visualize clusters in high dimensional data, Department of Computer Science, University of Marburg, Technical Report Nr. 36:1-12
- ↑ Ultsch, Alfred (2007). «Emergence in Self-Organizing Feature Maps». En Ritter, H.; Haschke, R., eds. Proceedings of the 6th International Workshop on Self-Organizing Maps (WSOM '07). Bielefeld, Germany: Neuroinformatics Group. ISBN 978-3-00-022473-7.
- ↑ a b Haykin, Simon (1999). «9. Self-organizing maps». Neural networks - A comprehensive foundation (2nd edición). Prentice-Hall. ISBN 0-13-908385-5.
- ↑ Kohonen, Teuvo (2005). «Intro to SOM». SOM Toolbox. Consultado el 18 de junio de 2006.
- ↑ Kohonen, Teuvo; Honkela, Timo (2011). «Kohonen network». Scholarpedia. Consultado el 24 de septiembre de 2012.
- ↑ Yin, Hujun; Learning Nonlinear Principal Manifolds by Self-Organising Maps, in Gorban, Alexander N.; Kégl, Balázs; Wunsch, Donald C.; and Zinovyev, Andrei (Eds.); Principal Manifolds for Data Visualization and Dimension Reduction, Lecture Notes in Computer Science and Engineering (LNCSE), vol. 58, Berlin, Germany: Springer, 2007, ISBN 978-3-540-73749-0
- ↑ Heskes, Tom; Energy Functions for Self-Organizing Maps, in Oja, Erkki; and Kaski, Samuel (Eds.), Kohonen Maps, Elsevier, 1999
- ↑ Kaski, Samuel (1997). «Data Exploration Using Self-Organizing Maps». Acta Polytechnica Scandinavica. Mathematics, Computing and Management in Engineering Series No. 82 (Espoo, Finland: Finnish Academy of Technology). ISBN 952-5148-13-0.
- ↑ Shah-Hosseini, Hamed; Safabakhsh, Reza (abril de 2003). «TASOM: A New Time Adaptive Self-Organizing Map». IEEE Transactions on Systems, Man, and Cybernetics—Part B: Cybernetics 33 (2): 271-282.
Enlaces externos[editar]
- Self-organizing maps for WEKA: Implementation of a self-organizing maps in Java, for the WEKA Machine Learning Workbench.
- Self-organizing maps for Ruby: Implementation of self-organizing maps in Ruby, for the AI4R project.
- Self-organizing map for JavaScript: An open-source implementation of a self-organizing map in JavaScript for node.js from Lucid Technics, LLC.
- Spice-SOM: A free GUI application of self-organizing map
- IFCSoft: An open-source Java platform for generating self-organizing maps
- Tutorial sobre las SOMs
- Recuperación de Información Archivado el 2 de abril de 2015 en Wayback Machine.
- Recuperación y Extracción de la Información no supervisada Archivado el 11 de abril de 2008 en Wayback Machine.
Software Libre[editar]
- Toolbox de SOMs para Matlab (incluye tutorial)
- LabSOM Laboratorio del SOM
- ViBlioSOM Visualización Bibliométrica mediante el SOM


















