Gramática formal
Una gramática formal es una estructura lógico-matemática con un conjunto de reglas de formación que definen las cadenas de caracteres admisibles en un determinado lenguaje formal o lengua natural. Las gramáticas formales aparecen en varios contextos diferentes: la lógica matemática, las ciencias de la computación y la lingüística teórica, frecuentemente con métodos e intereses divergentes.
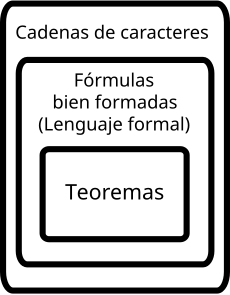
En un lenguaje formal, a las cadenas formadas según las reglas de la gramática formal se las llama fórmulas bien formadas, y el conjunto de todas las fórmulas bien formadas constituye un lenguaje formal. Una gramática formal no describe el significado de las fórmulas bien formadas, sino solamente su forma. La teoría de los lenguajes formales estudia las gramáticas formales y los lenguajes formales, y es una rama de la matemática aplicada. Sus aplicaciones se encuentran en la ciencia computacional teórica, la lingüística, la semántica formal, la lógica matemática y otras áreas.
Introducción[editar]
Una gramática formal es un conjunto de reglas para reescribir cadenas de caracteres, junto con un símbolo inicial desde el cual debe comenzar la reescritura. Por lo tanto, una gramática formal generalmente se piensa como una generadora de lenguajes. Sin embargo, a veces también puede ser usada como la base para un "reconocedor": una función que determina si una cadena cualquiera pertenece a un lenguaje o es gramaticalmente incorrecta.
Hay distintos tipos de gramáticas formales que generan lenguajes formales (véase la jerarquía de Chomsky). Imaginemos una gramática con estas dos reglas:
- A → bA
- A → c
El elemento en mayúsculas es el símbolo inicial. Los elementos en minúsculas son los símbolos terminales. Para generar cadenas de caracteres, la idea es sustituir el símbolo inicial de la izquierda por los símbolos de la derecha, y luego repetir el proceso hasta que sólo haya símbolos terminales. Por ejemplo:
- A → bA → bbA → bbbA → bbbc
Esta gramática da lugar a un lenguaje formal que consiste en el conjunto de todas las cadenas de caracteres que pueden ser generadas por medio ellas. Por ejemplo: bbbc, bbbbbbbbc, c, bc, etc.
Para comprender mejor la idea, podemos considerar un modelo de reescritura para el español:
- O → SUJ PRED (Oración → Sujeto Predicado)
- SUJ → Det N (Sujeto → Determinante Nombre)
- PRED → V COMP (Predicado → Verbo Complemento)
- DET → el
- N → niño, (hombre, anciano)
- V → duerme, (ríe, come)
- COMP → plácidamente, (intranquilo)
Estas reglas pueden utilizarse para generar la frase "el niño duerme plácidamente", así:
- O(RACIÓN) (símbolo inicial)
- SUJ(ETO) PRED(ICADO) (por la regla 1)
- DET(ERMINANTE) N(OMBRE) PRED(ICADO) (por la regla 2)
- DET(ERMINANTE) N(OMBRE) V(ERBO) COMP(LEMENTO) (por la regla 3)
- el N(OMBRE) V(ERBO) COMP(LEMENTO) (por la regla 4)
- el niño V(ERBO) COMP(LEMENTO) (por la regla 5)
- el niño duerme COMP(LEMENTO) (por la regla 6)
- el niño duerme plácidamente (por la regla 7)
Vemos que existen unas definiciones especiales como ORACIÓN, SUJETO, etc. que no aparecen en la frase final formada. Son unas entidades abstractas denominadas "categorías sintácticas" que no son utilizables en una oración (tienen un papel similar al de las categorías gramaticales de las lenguas naturales). E igualmente el mismo sistema permite derivar otras oraciones similares usando formas las formas léxicas entre paréntesis:
Det N V COMP El niño
hombre
ancianoduerme
ríe
comeplácidamente
intranquilo
Las categorías sintácticas definen la estructura del lenguaje representando porciones más o menos grandes de las frases. Existe una jerarquía interna entre las categorías sintácticas.
La categoría superior sería la FRASE que representa una oración válida en lengua castellana.
Por debajo de ella se encuentran sus componentes. Ninguna de estas categorías dan lugar a frases válidas solo la categoría superior.
Al finalizar toda la jerarquía llegamos a las palabras que son las unidades mínimas con significado que puede adoptar una frase.
Aplicando las jerarquías y sustituyendo elementos, llegamos al punto en donde todas las categorías sintácticas se han convertido en palabras, obteniendo por tanto una oración válida; como por ejemplo: El niño corre. Este proceso se llama producción o generación.
Gramáticas formales en lingüística teórica[editar]
Una gramática formal es un modelo matemático (más exactamente una estructura algebraica) compuesto por una serie de categorías sintácticas que se combinan entre sí por medio de unas reglas sintácticas que definen cómo se crea una categoría sintáctica por medio de otras o símbolos de la gramática. Existen varios tipos de gramáticas formales históricamente importantes:
- Las gramáticas formales categoriales (C-gramáticas) que usan un análisis de abajo arriba y requieren el uso de etiquetas de categoría para cada secuencia formada o constituyente sintáctico propiamente dicho. Existe una única categoría superior que denota cadenas completas y válidas.
- Las gramáticas de estructura sintagmática (ES-gramáticas, en inglés PS-grammars) basadas en reglas de reescritura y con un análisis de arriba abajo. Al igual que las C-gramáticas se basan en la noción de constituyente sintáctico.
- Las gramáticas asociativas (por la izquierda) (A-gramáticas, en inglés LA-grammars), que usa usa un análisis de abajo arriba, que permiten un análisis de complejidad lineal, aunque ignoran el concepto de constituyente sintáctico.
Los dos primeros tipos tienen puntos de conexión obvia con la noción de constituencia sintáctica y el análisis mediante árboles sintácticos. Sin embargo, los analizadores sintácticos para las oraciones formadas según ellas no pueden basarse en las reglas de generación (asimetría hablante-oyente), lo cual sugiere que no puedan ser buenos modelos de la intuición de los hablantes. Además los modelos de lengua natural basados en ellas parecen tener una complejidad polinómica o exponencial, lo cual no parece avenirse con la velocidad con que los hablantes procesan las lenguas naturales. En cambio las A-gramáticas en general tienen complejidad lineal, simetría entre hablantes y oyentes, sin embargo, ignoran los constituyentes clásicos del análisis sintáctico. Sin embargo, siguen siendo usadas para los analizadores sintácticos usados en computación.
Por medio de estos elementos constituyentes se define un mecanismo de especificación consistente en repetir el mecanismo de sustitución de una categoría por sus constituyentes en función de las reglas comenzando por la categoría superior y finalizando cuando la oración ya no contiene ninguna categoría. De esta forma, la gramática puede generar o producir cada una de las cadenas del lenguaje correspondiente y solo estas cadenas.
Definición de una C-gramática[editar]
Una gramática categorial o C-gramática es una basada en categorías gramaticales. Las formas léxicas y secuencias formadas a partir de ellas están etiquetadas con categorías que indican el tipo de entidad formada y sus posibilidades combinatorias (por ejemplo en una lengua nominal una secuencia de palabras puede constituir un sintagma nominal lo cual especifica con qué otro tipo de categorías puede combinarse este sintagma para formar otro sintagma mayor).
Las gramáticas categoriales se pueden definir como una estructura formal algebraica. Una gramática categorial es un quíntupla con las siguientes propiedades:
- (words) es el conjunto no vacío de formas bien formadas de la lengua (en una lengua natural W podría interpretarse como secuencias de fonemas que forman expresiones, irrespectivamente de su categoría gramatical).
- (categories) es el conjunto no vacío de categorías posibles. Para que este conjunto sea un conjunto de categorías aceptable se exige que si entonces también existan las categorías (frecuentemente denotada también como Y/X) y (frecuentemente denotada también como Y\X). Nótese que de lo anterior se desprende la existencia de las categorías y (sin más que intercambiar el papel de X e Y).
- El conjunto (lexicon) es un conjunto , este conjunto es algo diferente del lexicón convencional ya que incluye tanto palabras atómicas inanalizables como expresiones formadas a partir de ellas.
- El conjunto (rules) es un conjunto de reglas, generalmente formado por las siguientes dos reglas:
- Las anteriores se aplican a cualesquiera categorías y se interpretan así: si en un lenguaje formal los elementos a la izquierda de la regla pertenecen al lexicón , entonces la expresión a la derecha de la regla también es parte del lexicón (es decir, del conjunto de expresiones posibles en dicho lenguaje). Se comprende que puesto que la composición puede ser por la izquierda (regla 1) o por la derecha (regla 2) se haya requerido que el conjunto admita además de categorías e las categorías y .
- El conjunto (complete expresions)
Definición de una ES-gramática[editar]
En la definición clásica que dio Noam Chomsky en la década de 1950, una gramática formal de estructura sintagmática (ES-gramática) es una cuádrupla G = (N,T,S,P) donde:
- N es un conjunto finito de símbolos no terminales (variables).
- T es un conjunto finito de símbolos terminales (constantes), disjunto con N.
- S es un símbolo distinguido de N, el símbolo inicial.
- P es un conjunto finito de reglas de producción, cada una de la forma:
donde * es la clausura de Kleene. Esto es, cada regla de producción mapea de una cadena de símbolos a otra, donde la primera cadena contiene al menos un símbolo no terminal. En el caso de que la segunda cadena sea la cadena vacía, para evitar confusión se la denota con una notación especial (usualmente , o ).
El alfabeto de la gramática es entonces el conjunto
Derivaciones[editar]
Sea una gramática, y sean α, β, δ, φ, ρ, ... palabras de . Entonces:
- β se deriva de α en un paso de derivación, y lo denotamos con α β si existen dos cadenas , y una producción δ → ρ tales que α = δ , y β = ρ
- Notamos con al cierre reflexivo y transitivo de . Es decir α β denota a una secuencia de derivaciones en un número finito de pasos desde α hasta β.
- es una forma sentencial de , si puede obtenerse la siguiente secuencia de derivaciones . En el caso particular de que se dice que x es una sentencia
- Se denomina lenguaje formal generado por G al conjunto
Jerarquía de Chomsky[editar]
Cuando Noam Chomsky formalizó la idea de las gramáticas generativas en 1956, clasificó este tipo de gramáticas en varios tipos de complejidad creciente que forman la llamada jerarquía de Chomsky. La diferencia entre estos tipos es que cada uno de ellos tiene reglas más particulares y restringidas y por tanto generan lenguajes formales menos generales. Dos tipos importante son las gramáticas libres de contexto (Tipo 2) y las gramáticas regulares (Tipo 3). Las lenguas que pueden ser descritas mediante esos tipos de gramáticas son lenguas libres de contexto y lenguas regulares, respectivamente. Estos dos tipos son mucho menos generales que las gramáticas no restringidas de Tipo 0 (es decir, que pueden ser procesadas o reconocidas mediante máquinas de Turing). Estos dos tipos de gramáticas se usan más frecuentemente puesto que los analizadores sintácticos para estos lenguajes pueden implementarse de manera eficiente.[1] Por ejemplo, todas las lenguas regulares pueden ser reconocidas por un autómata finito. Para subconjuntos de gramáticas libres de contexto, existen algoritmos para generar analizadores sintácticos LL y analizadores sintácticos LR eficientes, que permiten reconocer los correspondientes lenguajes generados por esas gramáticas.
Limitación de las gramáticas formales[editar]
Las ES-gramáticas como la usada en los primeros modelos de gramática generativa requieren ciertas restricciones para ser computacionalmente tratables. Para entender esa restricción debe considerarse la interacción entre un hablante y un oyente, el primero genera una oración o secuencia de acuerdo con las reglas de la gramática, el segundo para entender dicha secuencia debe analizar la secuencia para entenderla, encontrando los elementos formantes, interpretándolos y reconstruyendo la relación hay entre ellos (estructura interna). Para que eso segundo sea posible se requiere que la estructura interna tenga una estructura suficientemente simple como poder analizar sintácticamente las secuencias con un bajo grado de ambigüedad. Pues bien computacionalmente se ha encontrado que la clase de complejidad frente al análisis inverso de ciertas gramáticas es excesiva. Para ES-gramáticas basadas en reglas de reescritura se tiene:
| Restricciones en las reglas |
Tipo de ES-gramática |
Tipo de lenguaje |
Grado de complejidad |
|---|---|---|---|
| tipo 3 | Gramática ES regular | lenguajes regulares | lineal |
| tipo 2 | Gramática ES libre de contexto |
lenguajes libres de contexto |
polinómica |
| tipo 1 | Gramática ES dependiente del contexto |
lenguajes dependientes del contexto |
exponencial |
| tipo 0 | Gramática ES no restringida |
lenguajes recursivamente enumerables |
indecidible |
Gramáticas formales en matemáticas y lógica[editar]
Dentro del enfoque formalista y axiomático de las matemáticas se concibió que ciertas áreas de las matemáticas podían concebirse como un sistema lógico-deductivo de fórmulas sujetas a restricciones de manipulación. La gramática formal de esos sistemas sería el conjunto de reglas combinatorias acordes a ciertos principios deductivos.
Un lenguaje formal en lógica o matemáticas es una tripleta donde denota el alfabeto o conjunto de signos usados, el conjunto de reglas explica qué combinaciones de signos están bien definidas y permite definir lo que es una fórmula bien formada (en ese sentido define la morfología de las palabras de la lengua formal). El conjunto de fórmulas bien formadas constituyen el vocabulario o léxico, mientras el par describe el conjunto de axiomas y el conjunto de reglas de deducción válidas. Estas dos últimas permiten establecer secuencias de fórmulas bien formadas (palabras del lenguaje formal) que constituyen demostraciones válidas dentro del sistema formal (son de alguna manera el equivalente a la sintaxis de la lengua formal).
Véase también[editar]
Referencias[editar]
- ↑ Grune, Dick & Jaacobs, Ceriel H., Parsing Techniques – A Practical Guide, Ellis Horwood, England, 1990.
Bibliografía[editar]
Hausser, Roland R. (1999). Foundations of Computational Linguistics (en inglés). Springer-Verlag. ISBN 3-540-66015-1.





































