Bisectriz

Construcción gráfica con regla y compás.

La bisectriz de un ángulo es la recta que lo divide en dos partes iguales. Es el lugar geométrico de los puntos del plano que equidistan (están a la misma distancia) de las semirrectas de un ángulo.

Características

Los puntos de la bisectriz son equidistantes a los dos lados (rectas) del ángulo. Recíprocamente, dos rectas, al cruzarse, determinan cuatro ángulos y cada uno de ellos define una bisectriz. Estas bisectrices resultan ser el lugar geométrico de los puntos equidistantes.

En la figura, la bisectriz interior al ángulo xOy (en amarillo) es (zz'), y la exterior es (ww'). Se cortan formando un ángulo recto. En efecto, si llamemos a la medida de xOz, y b la de yOw, observamos que 2a + 2b es la medida del ángulo xOx' , que es plano. Dividimos por 2: zOw mide a + b = 90º.

Aplicación en triángulos

Las tres bisectrices de los ángulos internos de un triángulo se cortan en un único punto, que equidista de los lados. Este punto se llama el incentro del triángulo y es el centro de la circunferencia inscrita al triángulo. Esta circunferencia es tangente a cada uno de los lados del triángulo.

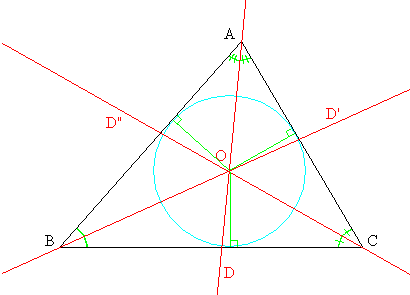
Demostración: Dos bisectrices del triángulo no pueden ser paralelas. Sea O la intersección de las bisectrices D y D' (ver figura). Como O pertenece a D, es equidistante de las rectas (AB) y (AC). Como O pertenece a D', entonces también equidista de las rectas (AB) y (BC). Por transitividad de la igualdad, es equidistante de (AC) y (BC), y pertenece a la bisectriz (interior) del ángulo C, es decir a D". Al ser equidistante a los tres lados. Se sigue que la circunferencia cuyo radio sea justamente la distancia común del punto O a los lados del triángulo es tangente a cada uno de los lados.

Propiedades

Considere el triángulo ABC y la circunferencia circunscrita. La mediatriz MN, del lado BC corta el arco BMC en su punto medio. Como el ángulo inscrito BAC subtiende dicho arco, los ángulos BAM y MAC son iguales y la recta AM resulta ser la bisectriz del ángulo BAC. Las rectas AN y AM son ortogonales, porque el lado MN del triángulo AMN es diámetro de la circunferencia y el vértice A se halla sobre dicha circunferencia. La recta AN es bisectriz del ángulo exterior al triángulo ABC en el vértice A. Por lo anteriormente expuesto, se puede decir: La mediatriz de un lado de un triángulo y las bisectrices del ángulo opuesto se intersectan sobre la circunferencia circunscrita

Este hecho se usa en la discusión de la circunferencia de los nueve puntos

Véase también

• Teorema de la bisectriz
• Mediatriz

Enlaces externos

• Bisectriz de un ángulo, en wikiEducared