Diferencia entre revisiones de «Triángulo de Pascal»
Página blanqueada |
m Revertidos los cambios de 200.27.103.140 a la última edición de Diegusjaimes |
||
| Línea 1: | Línea 1: | ||
[[imagen:triángulo de Pascal.png|thumb|330px|Triángulo de Pascal o de Tartaglia]] |
|||
El '''triángulo de [[Blaise Pascal|Pascal]]''' en [[matemáticas]] es un conjunto [[infinito]] de [[número entero|números enteros]] ordenados en forma de [[triángulo]] que expresan [[coeficientes binomiales]]. El interés del Triángulo de Pascal radica en su aplicación en [[álgebra]] y permite calcular de forma sencilla [[números combinatorios]] lo que sirve para aplicar el [[binomio de Newton]]. |
|||
También es conocido como '''Triángulo de [[Niccolò Fontana|Tartaglia]]'''. En países orientales como [[China]], [[India]] o [[Persia]], este triángulo se conocía y fue estudiado por matemáticos como [[Al-Karaji]], cinco siglos antes de que Pascal expusiera sus aplicaciones. En China es conocido como '''Triángulo de Yanghui'''. |
|||
== Composición del Triángulo de Pascal == |
|||
[[Archivo:PascalTriangleAnimated2.gif|right|150px]] |
|||
El Triángulo se construye de la siguiente manera: escribimos el número «1» centrado en la parte superior; después, escribimos una serie de números «1» en las casillas situadas en sentido diagonal descendente, a ambos lados; sumamos las parejas de cifras situadas horizontalmente (1 + 1), y el resultado (2) lo escribimos debajo de dichas casillas; continuamos el proceso escribiendo en las casillas inferiores la suma de las dos cifras situadas sobre ellas (1 + 2 = 3)... |
|||
Las cifras escritas en las filas, tales como: «1 2 1» y «1 3 3 1» recuerdan los coeficientes de las identidades: |
|||
::<math>(a+b)^2 = a^2 + 2ab + b^2 \quad</math> |
|||
::<math>(a+b)^3 = a^3 + 3a^2b +3ab^2+ b^3 \quad</math> |
|||
pues son los coeficientes de sus [[monomio]]s y, además, se puede generalizar para cualquier potencia del [[binomio]]: <math>(a+b)\quad</math> |
|||
==Vínculo entre el triángulo de Pascal y el binomio de Newton== |
|||
La expresión que proporciona las potencias de una suma '''<math>(a+b)^n\;</math>''' se denomina [[Binomio de Newton]]. |
|||
{{ecuación|<math>(a+b)^n=\sum_{k=0}^n{n \choose k}a^{n-k}b^k\quad\qquad \quad \and \quad 0 \le k \le n; \quad\ n,k \in \mathbb {N}</math>|1|left}} |
|||
En esta expresión, lo único que se desconoce son los coeficientes de los monomios. |
|||
{{teorema|Los coeficientes de la forma desarrollada de (a + b)<sup>n</sup> se encuentran en la línea «n + 1» del Triángulo de Pascal.}} |
|||
Hemos visto que era cierto para n = 2 y n = 3; también lo es para n = 0: (a + b+ w+ d)<sup>o</sup> = 1 = '''1'''·a<sup>o</sup>b<sup>0</sup> y con n = 1: (a + b)¹ = a + b = '''1'''·a + '''1'''·b.<br /> |
|||
Para obtener el resultado de cualquier valor de n ∈ '''N''', se procede por [[inducción matemática]]. Suponiendo que es cierto para un valor de '''n''', deducimos que lo es también para '''n+1'''. Observemos lo que sucede con n = 4. |
|||
[[imagen:triángulo Pascal binomio Newton.png|center]] |
|||
El desarrollo de (a + b)<sup>4</sup> consiste en el desarrollo de (a + b) (a + b)³. |
|||
Si sólo se escriben los coeficientes, obtenemos la siguiente suma: |
|||
[[imagen:triángulo Pascal binomio Newton 2.png|center]] |
|||
Obviamente, aparecen las mismas cifras desplazadas en una posición: la [[sumar|suma]] consiste en añadir a un coeficiente el coeficiente situado a su derecha, y esto es justamente lo que se obtiene en el triángulo de Pascal. |
|||
==Coeficientes del binomio de Newton== |
|||
[[imagen:triángulo de Pascal en tabla.png|right]] |
|||
Se inscribe el triángulo de Pascal en una [[tabla]] para poder nombrar a cada coeficiente del mismo. El número en la línea ''n'' y la columna ''p'' se denota: |
|||
<br/> |
|||
{| |
|||
|<math>n \choose p</math> |
|||
| o más raramente |
|||
|<math>C_n^p</math> |
|||
|} |
|||
(''"C"'' por ''"combinación"'') y se dice ''"n sobre p"'', "'combinación de n en p"' ó ''"coeficiente binomial n, p"''. Las casillas vacías corresponden a valores nulos. Por definición misma, tenemos, (para todo ''n'' natural): |
|||
{| |
|||
|<math> (a+b)^n = \sum_{p=0}^n {n\choose p} a^{n-p} b^p </math> |
|||
|} |
|||
para cualquier valor de ''a'' y ''b''. De hecho, es una igualdad de [[polinomio]]s en Z[a, b]. Sin perder en generalidad, resulta a veces más práctica la ''"definición"'' : |
|||
{| |
|||
|<math> (X+1)^n = \sum_{p=0}^n {n\choose p} X^p </math> |
|||
|} |
|||
vista como una igualdad de polinomios en Z[X]. De esta fórmula se deducen dos consecuencias: |
|||
{| |
|||
|Tomando X = 1 se obtiene: |
|||
|<math>\sum_{p=0}^n {n\choose p} = 2^n </math> |
|||
|} |
|||
La suma de los coeficientes de una misma línea vale 2<sup>n</sup>. En efecto: 1 = 2<sup>0</sup>, 1 + 1 = 2 = 2¹, 1 + 2 + 1 = 4 = 2², 1 + 3 + 3 + 1 = 8 = 2³, 1 + 4 + 6 + 4 + 1 = 16 = 2<sup>4</sup> ... · Con X = -1 se obtiene, (n > 0): |
|||
{| |
|||
|<math>\sum_{p=0}^n {n\choose p} (-1)^p = 0 </math> |
|||
| : la suma alterna de los números de una misma línea vale 0. |
|||
|} |
|||
En efecto: 1 - 1 = 0, 1 - 2 + 1 = 0, 1 - 3 + 3 - 1 = 0, 1 - 4 + 6 - 4 + 1 = 0, 1 - 5 + 10 - 10 + 5 - 1 = 0 ... Las propiedades que hemos observado en el triángulo se pueden ahora escribir con todo rigor: |
|||
{| align=left width=4% border=1 |
|||
| bgcolor=#FFFF00 |. |
|||
|} |
|||
{| |
|||
|<math> {n\choose 0} = {n\choose n} = 1</math> |
|||
| (costados izquierdos y derechos del triángulo). |
|||
|} |
|||
{| align=left width=4% border=1 |
|||
| bgcolor=#00FF00 |. |
|||
|} |
|||
{| |
|||
|<math> {n\choose 1} = {n\choose {n-1}} = n</math> |
|||
| (''"segunda capa"''). |
|||
|} |
|||
{| align=left width=4% border=1 |
|||
| bgcolor=#FF0000 |. |
|||
|} |
|||
{| |
|||
|<math> {n\choose {n-p}} = {n\choose p} </math> |
|||
| (simetría respecto al eje vertical del triángulo). |
|||
|} |
|||
{| align=left width=4% border=1 |
|||
| bgcolor=#00FFFF |. |
|||
|} |
|||
{| |
|||
|<math> {n\choose p} = 0 </math> |
|||
|cuando '''p > n''' (corresponde a la zona fuera del triángulo). |
|||
|} |
|||
Y claro, la regla de construcción del triángulo da la relación fundamental de los coeficientes binomiales: |
|||
{| align=left width=4% border=1 |
|||
| bgcolor=#FF00FF |. |
|||
|} |
|||
<math> {n\choose p} + {n\choose {p+1}} = {{n+1}\choose {p+1}}</math> |
|||
[[imagen:triángulo de Pascal colores.png]] |
|||
==Interpretación en combinatoria== |
|||
Los [[Coeficiente binomial|coeficientes binomiales]] son la base misma de la [[combinatoria]]. Veamos por qué: |
|||
Tomemos de nuevo un [[binomio]], por ejemplo <math>(a+b)^3</math>, y desarrollémoslo, pero de una manera distinta del párrafo anterior: |
|||
::<math>(a+b)^3 = (a+b)\cdot (a+b) \cdot (a+b)</math><br /> |
|||
luego quitemos las paréntesis, pero sin cambiar el orden en los productos, es decir sin aplicar la [[conmutatividad]]:<br /> |
|||
::<math> (a+b)\cdot (a+b) \cdot (a+b)= (a a + ab + ba + bb )\cdot (a+b) </math><br /> |
|||
::<math> = aaa + aab + aba + abb + baa + bab + bba + bbb \quad </math> |
|||
Y agrupemos los términos que contienen el mismo número de a, (y de b): |
|||
::<math> = aaa + (aab + aba + baa) + (abb + bab + bba) + bbb \quad</math> |
|||
El primer [[Paréntesis|paréntesis]] contiene todas las palabras constituidas de un ''b'' y dos ''a''. En este caso, es fácil ver que hay exactamente tres. En el caso general, para contar las palabras, hay que aplicar la conmutatividad, pues las palabras que contienen el mismo número de a y b darán el mismo término: |
|||
::<math> = 1\cdot a^3 + 3\cdot a^2b + 3\cdot ab^2 + 1\cdot b^3 </math> |
|||
{| |
|||
|El primer factor 3, que es |
|||
|<math>{3 \choose 1}</math> |
|||
|cuenta las tres palabras mencionadas (aab, aba y baa). |
|||
|} |
|||
{| |
|||
|El segundo factor 3, que es |
|||
|<math>{3 \choose 2}</math> |
|||
|cuenta las palabras hechas de dos ''b'' y un ''a'' (abb, bab y bba). |
|||
|} |
|||
Obviamente, sólo hay una palabra de tres letras constituidas de ''a'' solamente, y esto corresponde al monomio '''1·a³''', con 1 = <math>{3 \choose 0}</math> ( «0 » por ''ninguna b''). |
|||
En vez de hablar de palabras formadas con ''a'' y ''b'', es equivalente imaginar una hilera de ''n'' cajones inicialmente vacíos, y ''p'' bolas intercambiables que se tienen que repartir, en cada [[cajón]] no cabiendo más de una. Se trata en todos casos de repartir ''p'' objetos entre ''n'' sitios posibles, o de escoger un grupo de ''p'' objetos/sitios entre ''n'' objetos/sitios. De ahí la apelación ''p entre n''. |
|||
Todo lo anterior lleva al '''teorema''': |
|||
{| |
|||
| Hay exactamente |
|||
|<math>{n \choose p}</math> |
|||
| maneras de escoger un conjunto de ''p'' elementos entre ''n'' elementos. |
|||
|} |
|||
En matemática formal, se prefiere hablar de [[conjunto]]s: |
|||
{| |
|||
|Existen |
|||
|<math>{n \choose p}</math> |
|||
|subconjuntos de cardinal p en un conjunto de cardinal n. |
|||
|} |
|||
Este punto de vista permite hallar la fórmula para los [[Distribución binomial|coeficientes binomiales]]. En efecto, para elegir el « primer » elemento, hay ''n'' posibilidades, luego para escoger el segundo quedan ''n-1'' posibilidades y así sucesivamente hasta el elemento número ''p'', que tiene ''n-p+1''. El orden en el que se ha elegido estos ''p'' elementos no importa, se podía haber obtenido el mismo [[subconjunto]] de ''p'' elementos en otro orden. Hay [[factorial|p!]] [[permutación y grupo simétrico|permutaciones]] posibles de estos ''p'' elementos, es decir p! maneras de obtener el mismo conjunto. |
|||
{| |
|||
| Por tanto hay |
|||
|<math> \frac {n \cdot (n-1) \cdot (n-2) ... (n-p+1)} {p!} </math> |
|||
|subconjuntos posibles. |
|||
|} |
|||
En conclusión: |
|||
<center> |
|||
<math> {n\choose p} = \frac {n \cdot (n-1) \cdot (n-2) ... (n-p+1)} {p \cdot (p-1) \cdot (p-2) ... 2 \cdot 1} = \frac {n!} {p! \cdot (n-p)!} </math> |
|||
</center> |
|||
Verifiquémoslo en un ejemplo: |
|||
{| |
|||
| |
|||
|<math>{5\choose 2} = \frac { 5!} {2! 3!} = \frac {5 \times 4 \times 3 \times 2} {2 \times 3 \times 2} = 10 </math> |
|||
|} |
|||
En el triángulo, el valor en la quinta línea y segunda columna es 10. Para rematar, listemos las palabras de cinco letras formadas de 2 ''a'' y 5-2 = 3 ''b'' (en el orden alfabético, o en el orden creciente considerando que ''a'' es la cifra ''0'' y ''b'' la cifra ''1''):<br /> |
|||
aabbb, ababb, abbab, abbba, baabb, babab, babba, bbaab, bbaba, bbbaa. |
|||
La fórmula permite verificar todas las propiedades del párrafo anterior, sin embargo se puede prescindir de los cálculos en la mayoría de los casos, con tal de manipular los conceptos idóneos. |
|||
[[imagen:partición_en_dos_de_un_conjunto.png|right]] |
|||
Un [[subconjunto]] A de E define una ''partición'' de E en dos partes E = A ∪ B , con A ∩ B = {}= ∅ ([[conjunto vacío]]). Aquí <math> B = \overline{A}</math> es el complementario de A en E. |
|||
Da lo mismo escoger los ''p'' elementos de A que los ''n-p'' elementos de <math>\overline{A}</math>.<br /> |
|||
{| |
|||
|Esto justifica, sin cálculo, la simetría |
|||
|<math>{n\choose {n-p}} ={ n\choose p}</math>. |
|||
|} |
|||
{| |
|||
|Si p > n, no hay subconjuntos de E con ''p'' elementos, porque E contiene sólo ''n'', luego |
|||
|<math> {n\choose p} = 0</math> |
|||
|} |
|||
{| |
|||
|También son evidentes las igualdades |
|||
|<math> {n\choose 1} = n</math> |
|||
| y |
|||
|<math> {n\choose 0} = 1</math> |
|||
| porque, en el primer caso, |
|||
|} |
|||
hay tantas maneras de escoger subconjunto de tamaño 1 que de elementos de E, y en el segundo caso, sólo existe un conjunto con cero elemento: el conjunto vacío. |
|||
La regla fundamental también tiene explicación gráfica: |
|||
Prueba: se escoge un elemento ''e'' cualquiera de ''E'', que contiene n+1 elementos: E = E' ∪ {e}. Luego se consideran los subconjuntos ''A'' de ''E'' de cardenal p+1. Son de dos tipos: o contienen e, o no. |
|||
{| |
|||
|Si ''e'' ∈ ''A'', entonces falta elegir ''p'' elementos de E' para completar ''A''. Hay |
|||
|<math> {n\choose p}</math> |
|||
| posibilidades. |
|||
|} |
|||
{| |
|||
|Si ''e'' ∉ A, entonces falta elegir ''p+1'' elementos de E' para definir ''A''. Hay |
|||
|<math> {n\choose {p+1}}</math> |
|||
| posibilidades. |
|||
|} |
|||
Sumando los dos casos, se obtiene todos las partes de p+1 elementos de E, constituido de n+1 elementos. |
|||
{| |
|||
|Hay por tanto |
|||
|<math> {{n+1}\choose {p+1}} = {n\choose {p+1}}+ {n\choose p}</math> |
|||
|} |
|||
Un ejemplo: |
|||
[[imagen:suma de binomiales figura.png]] |
|||
Aquí va una propiedad [[aritmética]], sin interpretación geométrica: cuando '''n es primo''', los coeficientes binomiales en la línea ''n'' son divisibles por ''n'', excepto los dos ''bordes'' de la misma (que valen 1). |
|||
Escrito formalmente: |
|||
'''Teorema:''' |
|||
{{teorema |
|||
|1= Si ''p'' es primo entonces ''p'' divide a <math>{p\choose k} </math> para ''k''=2,3,...,n-1. |
|||
}} |
|||
[[imagen:triángulo_de_Pascal_con_n_primo.png|right]] |
|||
En la figura, los ejemplos están en verde, y los contraejemplos (cuando n no es primo y p divide n) en amarillo. |
|||
{| |
|||
|'''Prueba''': en la fracción |
|||
|<math>\frac {n!} {p! (n-p)!} </math> |
|||
| el factor primo |
|||
|} |
|||
''n'' aparece una vez en el numerador y jamás en el denominador. |
|||
(El denominador es un producto de números entre 1 y n-1). Por tanto la fracción es divisible por n. |
|||
==Generalización== |
|||
En vez de considerar las potencias de '''a + b''', se puede mirar las del trinomio '''a + b + c'''. <br /> |
|||
'''(a + b + c)<sup>n</sup>''' es una suma de monomios de la forma ''λ<sub>p, q, r</sub> |
|||
·a<sup>p</sup>·b<sup>q</sup>·c<sup>r</sup>'', con ''p'', ''q'' y ''r'' positivos, ''p + q + r = n'', y λ<sub>p, q, r</sub> un natural que se tendría que llamar ''coeficiente trinomial''. |
|||
[[imagen:partición_de_un_conjunto.png|right]] |
|||
Los cálculos son similares a los del coeficiente binomial, y dan la expresión siguiente:<br /> |
|||
<math> \lambda_{p,q,r} = \frac {n!} {p! q! r!} </math> <br /> |
|||
Corresponde al número de partición en tres de un conjunto de ''n'' elementos, en subconjuntos de ''p'', ''q'' y ''r'' elementos. Un ejemplo: |
|||
[[imagen:pirámide_de_Pascal.png|left]] |
|||
Estos coeficientes se pueden hallar en la analogía tridimensional del triángulo de Pascal: Se podría llamar la ''[[pirámide de Pascal]]'', es también [[infinito|infinita]], con secciones triangulares, y el valor en cada casilla es la suma de los valores de las tres casillas encima de ella.<br /> |
|||
Se ha dibujado las primeras secciones a partir de la cumbre.<br /> |
|||
Se observa una invariante por rotación de 120 grados alrededor de un eje vertical que pasa por el vértice.<br /> |
|||
El triángulo de Pascal aparece en las tres caras de la pirámide. |
|||
Está claro que todo esto se puede generalizar a dimensiones finitas cualquieras, pero sin la posibilidad de hacer dibujos explicativos. |
|||
==Otra forma de dibujar el triángulo== |
|||
La ilustración al comienzo del artículo muestra el triángulo de Tartaglia o Pascal dibujado como un triángulo equilátero. Es posible «enderezarlo» de tal forma que su dibujo quede como un triángulo rectángulo. De esta forma, a la izquierda queda una columna de números «1». La siguiente columna deja un lugar vacío en la primera fila y sigue con la sucesión de números naturales: 1, 2, 3, 4, ..., n, .... La tercera columna deja dos filas vacías y comienza con la sucesión de los números triangulares: 1, 3, 6, 10, 15, .... Dibujado de esta manera es fácil ver que: |
|||
*Cada número en una columna cualquiera es igual a la suma parcial de los elementos de la columna anterior (a la izquierda) hasta la fila anterior en orden descendente. |
|||
*La tercera columna es la sucesión de los números triangulares; la cuarta, la de los números tetraédricos; la quinta, la de los números pentaédricos, y así sucesivamente. |
|||
== Enlaces externos == |
|||
{{commonscat|Pascal's triangle}} |
|||
{{EL}} |
|||
[[Categoría:álgebra]] |
|||
[[ar:مثلث باسكال]] |
|||
[[bg:Триъгълник на Паскал]] |
|||
[[ca:Triangle de Tartaglia]] |
|||
[[cs:Pascalův trojúhelník]] |
|||
[[da:Pascals trekant]] |
|||
[[de:Pascalsches Dreieck]] |
|||
[[en:Pascal's triangle]] |
|||
[[fa:مثلث خیام]] |
|||
[[fi:Pascalin kolmio]] |
|||
[[fr:Triangle de Pascal]] |
|||
[[gl:Triángulo de Pascal]] |
|||
[[he:משולש פסקל]] |
|||
[[hu:Pascal-háromszög]] |
|||
[[is:Pascal-þríhyrningur]] |
|||
[[it:Triangolo di Tartaglia]] |
|||
[[ja:パスカルの三角形]] |
|||
[[ko:파스칼의 삼각형]] |
|||
[[lt:Paskalio trikampis]] |
|||
[[mn:Паскалийн гурвалжин]] |
|||
[[ms:Segi tiga Pascal]] |
|||
[[nl:Driehoek van Pascal]] |
|||
[[no:Pascals trekant]] |
|||
[[pl:Trójkąt Pascala]] |
|||
[[pt:Triângulo de Pascal]] |
|||
[[ru:Биномиальный коэффициент#Треугольник Паскаля]] |
|||
[[simple:Pascal's Triangle]] |
|||
[[sr:Паскалов троугао]] |
|||
[[sv:Pascals triangel]] |
|||
[[tg:Секунҷаи Хайём-Паскал]] |
|||
[[tr:Pascal üçgeni]] |
|||
[[uk:Трикутник Паскаля]] |
|||
[[ur:خیام تکون]] |
|||
[[vi:Tam giác Pascal]] |
|||
[[zh:賈憲三角形]] |
|||
Revisión del 18:54 29 sep 2009

El triángulo de Pascal en matemáticas es un conjunto infinito de números enteros ordenados en forma de triángulo que expresan coeficientes binomiales. El interés del Triángulo de Pascal radica en su aplicación en álgebra y permite calcular de forma sencilla números combinatorios lo que sirve para aplicar el binomio de Newton.
También es conocido como Triángulo de Tartaglia. En países orientales como China, India o Persia, este triángulo se conocía y fue estudiado por matemáticos como Al-Karaji, cinco siglos antes de que Pascal expusiera sus aplicaciones. En China es conocido como Triángulo de Yanghui.
Composición del Triángulo de Pascal

El Triángulo se construye de la siguiente manera: escribimos el número «1» centrado en la parte superior; después, escribimos una serie de números «1» en las casillas situadas en sentido diagonal descendente, a ambos lados; sumamos las parejas de cifras situadas horizontalmente (1 + 1), y el resultado (2) lo escribimos debajo de dichas casillas; continuamos el proceso escribiendo en las casillas inferiores la suma de las dos cifras situadas sobre ellas (1 + 2 = 3)...
Las cifras escritas en las filas, tales como: «1 2 1» y «1 3 3 1» recuerdan los coeficientes de las identidades:
pues son los coeficientes de sus monomios y, además, se puede generalizar para cualquier potencia del binomio:
Vínculo entre el triángulo de Pascal y el binomio de Newton
La expresión que proporciona las potencias de una suma se denomina Binomio de Newton.
(1)
En esta expresión, lo único que se desconoce son los coeficientes de los monomios.
|
Hemos visto que era cierto para n = 2 y n = 3; también lo es para n = 0: (a + b+ w+ d)o = 1 = 1·aob0 y con n = 1: (a + b)¹ = a + b = 1·a + 1·b.
Para obtener el resultado de cualquier valor de n ∈ N, se procede por inducción matemática. Suponiendo que es cierto para un valor de n, deducimos que lo es también para n+1. Observemos lo que sucede con n = 4.
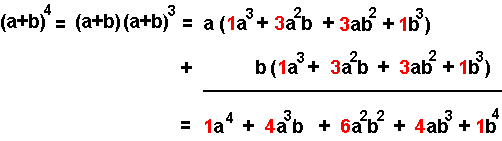
El desarrollo de (a + b)4 consiste en el desarrollo de (a + b) (a + b)³.
Si sólo se escriben los coeficientes, obtenemos la siguiente suma:

Obviamente, aparecen las mismas cifras desplazadas en una posición: la suma consiste en añadir a un coeficiente el coeficiente situado a su derecha, y esto es justamente lo que se obtiene en el triángulo de Pascal.
Coeficientes del binomio de Newton

Se inscribe el triángulo de Pascal en una tabla para poder nombrar a cada coeficiente del mismo. El número en la línea n y la columna p se denota:
| o más raramente |
("C" por "combinación") y se dice "n sobre p", "'combinación de n en p"' ó "coeficiente binomial n, p". Las casillas vacías corresponden a valores nulos. Por definición misma, tenemos, (para todo n natural):
para cualquier valor de a y b. De hecho, es una igualdad de polinomios en Z[a, b]. Sin perder en generalidad, resulta a veces más práctica la "definición" :
vista como una igualdad de polinomios en Z[X]. De esta fórmula se deducen dos consecuencias:
| Tomando X = 1 se obtiene: |
La suma de los coeficientes de una misma línea vale 2n. En efecto: 1 = 20, 1 + 1 = 2 = 2¹, 1 + 2 + 1 = 4 = 2², 1 + 3 + 3 + 1 = 8 = 2³, 1 + 4 + 6 + 4 + 1 = 16 = 24 ... · Con X = -1 se obtiene, (n > 0):
| : la suma alterna de los números de una misma línea vale 0. |
En efecto: 1 - 1 = 0, 1 - 2 + 1 = 0, 1 - 3 + 3 - 1 = 0, 1 - 4 + 6 - 4 + 1 = 0, 1 - 5 + 10 - 10 + 5 - 1 = 0 ... Las propiedades que hemos observado en el triángulo se pueden ahora escribir con todo rigor:
| . |
| (costados izquierdos y derechos del triángulo). |
| . |
| ("segunda capa"). |
| . |
| (simetría respecto al eje vertical del triángulo). |
| . |
| cuando p > n (corresponde a la zona fuera del triángulo). |
Y claro, la regla de construcción del triángulo da la relación fundamental de los coeficientes binomiales:
| . |
Interpretación en combinatoria
Los coeficientes binomiales son la base misma de la combinatoria. Veamos por qué: Tomemos de nuevo un binomio, por ejemplo , y desarrollémoslo, pero de una manera distinta del párrafo anterior:
luego quitemos las paréntesis, pero sin cambiar el orden en los productos, es decir sin aplicar la conmutatividad:
Y agrupemos los términos que contienen el mismo número de a, (y de b):
El primer paréntesis contiene todas las palabras constituidas de un b y dos a. En este caso, es fácil ver que hay exactamente tres. En el caso general, para contar las palabras, hay que aplicar la conmutatividad, pues las palabras que contienen el mismo número de a y b darán el mismo término:
| El primer factor 3, que es | cuenta las tres palabras mencionadas (aab, aba y baa). |
| El segundo factor 3, que es | cuenta las palabras hechas de dos b y un a (abb, bab y bba). |
Obviamente, sólo hay una palabra de tres letras constituidas de a solamente, y esto corresponde al monomio 1·a³, con 1 = ( «0 » por ninguna b).
En vez de hablar de palabras formadas con a y b, es equivalente imaginar una hilera de n cajones inicialmente vacíos, y p bolas intercambiables que se tienen que repartir, en cada cajón no cabiendo más de una. Se trata en todos casos de repartir p objetos entre n sitios posibles, o de escoger un grupo de p objetos/sitios entre n objetos/sitios. De ahí la apelación p entre n.
Todo lo anterior lleva al teorema:
| Hay exactamente | maneras de escoger un conjunto de p elementos entre n elementos. |
En matemática formal, se prefiere hablar de conjuntos:
| Existen | subconjuntos de cardinal p en un conjunto de cardinal n. |
Este punto de vista permite hallar la fórmula para los coeficientes binomiales. En efecto, para elegir el « primer » elemento, hay n posibilidades, luego para escoger el segundo quedan n-1 posibilidades y así sucesivamente hasta el elemento número p, que tiene n-p+1. El orden en el que se ha elegido estos p elementos no importa, se podía haber obtenido el mismo subconjunto de p elementos en otro orden. Hay p! permutaciones posibles de estos p elementos, es decir p! maneras de obtener el mismo conjunto.
| Por tanto hay | subconjuntos posibles. |
En conclusión:
Verifiquémoslo en un ejemplo:
En el triángulo, el valor en la quinta línea y segunda columna es 10. Para rematar, listemos las palabras de cinco letras formadas de 2 a y 5-2 = 3 b (en el orden alfabético, o en el orden creciente considerando que a es la cifra 0 y b la cifra 1):
aabbb, ababb, abbab, abbba, baabb, babab, babba, bbaab, bbaba, bbbaa.
La fórmula permite verificar todas las propiedades del párrafo anterior, sin embargo se puede prescindir de los cálculos en la mayoría de los casos, con tal de manipular los conceptos idóneos.

Un subconjunto A de E define una partición de E en dos partes E = A ∪ B , con A ∩ B = {}= ∅ (conjunto vacío). Aquí es el complementario de A en E.
Da lo mismo escoger los p elementos de A que los n-p elementos de .
| Esto justifica, sin cálculo, la simetría | . |
| Si p > n, no hay subconjuntos de E con p elementos, porque E contiene sólo n, luego |
| También son evidentes las igualdades | y | porque, en el primer caso, |
hay tantas maneras de escoger subconjunto de tamaño 1 que de elementos de E, y en el segundo caso, sólo existe un conjunto con cero elemento: el conjunto vacío.
La regla fundamental también tiene explicación gráfica:
Prueba: se escoge un elemento e cualquiera de E, que contiene n+1 elementos: E = E' ∪ {e}. Luego se consideran los subconjuntos A de E de cardenal p+1. Son de dos tipos: o contienen e, o no.
| Si e ∈ A, entonces falta elegir p elementos de E' para completar A. Hay | posibilidades. |
| Si e ∉ A, entonces falta elegir p+1 elementos de E' para definir A. Hay | posibilidades. |
Sumando los dos casos, se obtiene todos las partes de p+1 elementos de E, constituido de n+1 elementos.
| Hay por tanto |
Un ejemplo:
Aquí va una propiedad aritmética, sin interpretación geométrica: cuando n es primo, los coeficientes binomiales en la línea n son divisibles por n, excepto los dos bordes de la misma (que valen 1). Escrito formalmente:
Teorema:
|

En la figura, los ejemplos están en verde, y los contraejemplos (cuando n no es primo y p divide n) en amarillo.
| Prueba: en la fracción | el factor primo |
n aparece una vez en el numerador y jamás en el denominador. (El denominador es un producto de números entre 1 y n-1). Por tanto la fracción es divisible por n.
Generalización
En vez de considerar las potencias de a + b, se puede mirar las del trinomio a + b + c.
(a + b + c)n es una suma de monomios de la forma λp, q, r
·ap·bq·cr, con p, q y r positivos, p + q + r = n, y λp, q, r un natural que se tendría que llamar coeficiente trinomial.

Los cálculos son similares a los del coeficiente binomial, y dan la expresión siguiente:
Corresponde al número de partición en tres de un conjunto de n elementos, en subconjuntos de p, q y r elementos. Un ejemplo:

Estos coeficientes se pueden hallar en la analogía tridimensional del triángulo de Pascal: Se podría llamar la pirámide de Pascal, es también infinita, con secciones triangulares, y el valor en cada casilla es la suma de los valores de las tres casillas encima de ella.
Se ha dibujado las primeras secciones a partir de la cumbre.
Se observa una invariante por rotación de 120 grados alrededor de un eje vertical que pasa por el vértice.
El triángulo de Pascal aparece en las tres caras de la pirámide.
Está claro que todo esto se puede generalizar a dimensiones finitas cualquieras, pero sin la posibilidad de hacer dibujos explicativos.
Otra forma de dibujar el triángulo
La ilustración al comienzo del artículo muestra el triángulo de Tartaglia o Pascal dibujado como un triángulo equilátero. Es posible «enderezarlo» de tal forma que su dibujo quede como un triángulo rectángulo. De esta forma, a la izquierda queda una columna de números «1». La siguiente columna deja un lugar vacío en la primera fila y sigue con la sucesión de números naturales: 1, 2, 3, 4, ..., n, .... La tercera columna deja dos filas vacías y comienza con la sucesión de los números triangulares: 1, 3, 6, 10, 15, .... Dibujado de esta manera es fácil ver que:
- Cada número en una columna cualquiera es igual a la suma parcial de los elementos de la columna anterior (a la izquierda) hasta la fila anterior en orden descendente.
- La tercera columna es la sucesión de los números triangulares; la cuarta, la de los números tetraédricos; la quinta, la de los números pentaédricos, y así sucesivamente.
Enlaces externos
 Wikimedia Commons alberga una categoría multimedia sobre Triángulo de Pascal.
Wikimedia Commons alberga una categoría multimedia sobre Triángulo de Pascal.- El contenido de este artículo incorpora material de una entrada de la Enciclopedia Libre Universal, publicada en español bajo la licencia Creative Commons Compartir-Igual 3.0.








































