Baricentro

En geometría, el baricentro o centroide de una superficie contenida en una figura geométrica plana, es un punto tal, que cualquier recta que pasa por él, divide a dicha superficie en dos partes de igual área. En física, se puede correspoder con el centro de masas de superficies que poseen características homogéneas.

Sean A₁,... A_n n puntos, y m₁,... m_n n, números (m como masa ). Entonces el baricentro de los ( A_i, m_i ) es el punto G definido como sigue:

${\overrightarrow {OG\,}}={\frac {\sum {m_{i}{\overrightarrow {O\!A_{i}}}}}{\sum {m_{i}}}}={\frac {m_{1}{\overrightarrow {O\!A_{1}}}+...+m_{n}{\overrightarrow {O\!A_{n}}}}{m_{1}+...+m_{n}}},\quad {\mbox{con}}\quad \sum {m_{i}}\neq 0$

Esta definición depende del punto O, que puede ser cualquiera. Si se toma el origen del plano o del espacio, se obtiene las coordenadas del baricentro, como promedio ponderado por los mi, de las coordenadas de los puntos Ai:

$x_{G}={\frac {\sum {m_{i}x_{i}}}{\sum {m_{i}}}}={\frac {m_{1}x_{1}+...+m_{n}x_{n}}{m_{1}+...+m_{n}}}$

La definición anterior no equivale a la fórmula siguiente, mucho menos práctica para el cálculo vectorial, pues prescinde de las fracciones (se obtiene tomando O = G):

$\sum _{i=1}^{n}{m_{i}{\overrightarrow {G\!A_{i}}}}={\vec {0}}\quad {\mbox{o bien}}\quad m_{1}{\overrightarrow {G\!A_{1}}}+...+m_{n}{\overrightarrow {G\!A_{n}}}={\vec {0}}$

Un isobaricentro (iso: mismo) es un baricentro con todas las masas iguales entre sí; es usual en tal caso tomarlas iguales a 1. Si no se precisan las masas, el baricentro es por defecto el isobaricentro.

El baricentro coincide con la noción física de centro de gravedad, también llamado centro de masas, en algunos casos como:

• El baricentro de {A, B} es el centro de masa del segmento [A;B], o sea de una barra de extremos A y B, de masa uniformemente distribuida.
• El baricentro de {A, B, C} es el centro de gravedad del triángulo ABC, suponiéndole una densidad superficial uniforme (por ejemplo, al recortar un triángulo en una hoja de cartón). Corresponde al punto donde se cortan las medianas. El triángulo de cartón se mantendrá en equilibro (inestable) en la punta de un lápiz o de un compás si éste está colocado justo debajo del centro de masa. El baricentro de un triángulo tiene además la propiedad de pertenecer a la recta de Euler.
• El baricentro de cuatro puntos {A, B, C, D} del espacio es el centro de gravedad del tetraedro, suponiéndole una densidad volúmica uniforme. Corresponde al punto donde se cortan los segmentos que unen cada vértice con el isobaricentro de la cara opuesta.

Se puede generalizar lo anterior en cualquier dimensión.

La coincidencia del baricentro y el centro de gravedad permite localizar el primero de una forma sencilla. Si tomamos el pedazo de cartón antes comentado y lo sujetamos verticalmente desde cualquiera de sus puntos, girará hasta que el centro de gravedad (baricentro) se sitúe justamente en la vertical del punto de sujeción; marcando dicha vertical sobre el cartón y repitiendo el proceso sujetando desde un segundo punto, encontraremos el baricentro en el punto de intersección.

Propiedades topológicas:

El baricentro G de (A, a) y (B, b) con a y b cualesquiera, está ubicado en la recta (AB). Si a y b son ambos positivos, G pertenece al segmento [A,B]. En este caso los coeficientes a y b se pueden leer en el gráfico. Por ejemplo:

${\overrightarrow {AG\,}}={5 \over 7}\,{\overrightarrow {GB\,}}\quad \Leftrightarrow \quad 7\,{\overrightarrow {AG\,}}=5\,{\overrightarrow {GB\,}}\quad \Leftrightarrow \quad 7\,{\overrightarrow {GA\,}}+5\,{\overrightarrow {GB\,}}={\vec {0}}$

Y por lo tanto G = bar { (A, 7), (B, 5) }. Basta pues con permutar las longitudes del gráfico para obtener las masas de los puntos.

El baricentro G de tres puntos del espacio (A, a), (B, b) y (C, c) con a, b y c cualesquiera está ubicado en el plano (ABC). Si son todos positivos, G pertenece al triángulo ABC. Por supuesto, estas propiedades se generalizan a todas las dimensiones.

Propiedades algebraicas:

• Homogeneidad: no cambia el baricentro si se multiplica todas las masas por un mismo factor k ≠ 0.

formalmente: bar { (A₁, m₁), ..., (A_n, m_n) } = bar { (A₁, km₁), ..., (A_n, km_n) }.

• Asociatividad: el baricentro se puede calcular reagrupando puntos, es decir introduciendo baricentros parciales.

Por ejemplo, si D = bar {(A, a), (B, b)} (con a + b ≠ 0) entonces bar {(A, a), (B, b), (C, c)} = bar {(D,a + b), (C, c)} (a + b + c ≠ 0)

Ejemplo de demostración: Consideremos de nuevo el centro de masa de un triángulo ABC. Llamemos I el centro del segmento [B,C]. Entonces I = bar { (B, 1), (C, 1)}. Luego G = bar {(A, 1), (B, 1), (C, 1)} = bar {(A, 1), (I, 2)}, lo que significa que G está en el segmento [A,I], a un tercio del camino a partir de I.

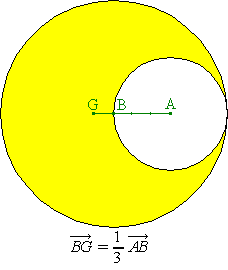
El baricentro se puede definir en las matemáticas con coeficientes negativos. Como no existen masas negativas, ¿ qué significado físico se puede atribuir a estos cálculos ? He aquí un ejemplo muy sencillo: en una hoja de cartón, recortemos una medialuna como lo muestra la figura que sigue, constituido de un círculo en el cual hemos quitado otro círculo de radio dos veces menor. Nos preguntamos cual es el centro de masa del creciente.

El cálculo resulta muy simplificado si consideramos la medialuna como una yuxtaposición de dos discos, uno grande con masa positiva, y el otro, pequeño, con masa negativa. Las masas son proporcionales a las áreas (densidad uniforme), lo que da una masa de 4 para el primer disco, y de -1 para el segundo. Entonces G = bar {(A, -1), (B, 4)}.

Cálculo geométrico del baricentro:

El cálculo geométrico (con regla y compás) del baricentro de una forma rápida de un polígono (regular o irregular), se puede realizar de la siguiente forma:

Si tenemos un polígono de n vértices,

• Descomponer el polígono en triángulos y cuadriláteros disjuntos (que no tengan vértices en común)
• Calcular los baricentros de estos triángulos y cuadriláteros, y formar el polígono correspodiente
• Volver al primer paso

Se puede probar que este algoritmo tiene orden logarítmico.

Véase también

• Centroide
• Centro de gravedad
• Centro de masas
• Teorema del centroide de Pappus