Artefactos de anillo


En procesamiento de señales y, particularmente en procesamiento digital de imágenes, los artefactos de anillo son artefactos que aparecen como señales espurias cerca de transiciones bruscas en una señal. Visualmente, aparecen como bandas o "fantasmas" cerca de bordes; En audición, aparecen como "ecos" cerca de transiciones, particularmente sonidos de instrumentos de percusión; los más notables son los pre-ecos. Como con otros artefactos, su minimización es clave en el diseño de filtros.
Introducción[editar]
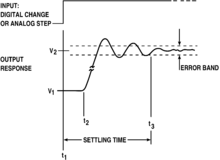
La existencia de artefactos de anillo está causada por una señal sometida a una limitación de banda (específicamente, no teniendo altas frecuencias) o que pasa a través de un filtro pasa bajo. Esta es la explicación en el dominio de la frecuencia. En términos del dominio del tiempo, la causa de este tipo de anillos es por la ondulación en la función sinc,[1] la cual es la respuesta a impulso (representación del dominio del tiempo) de un filtro pasa bajo perfecto. Matemáticamente, a esto se le denomina fenómeno de Gibbs
Se puede distinguir el rebasamiento superior (e inferior), que ocurre cuando se acentúan las transiciones del anillo – la salida es más alta que la entrada – donde, después de un rebasamiento, la señal se sobre-corrige y es ahora menor del valor objetivo; estos fenómenos ocurren juntos y, a menudo se vinculan para referirse a ellos como "anillamiento"
El término "anillamiento" se usa habitualmente para los rizados en el dominio de tiempo, aunque a veces se usa también para los efectos del dominio de frecuencia:[2] representando un filtro en el dominio de tiempo por una función rectangular, causa rizados en el dominio de frecuencia por la misma razón que un filtro pasa bajo (función rectangular en el dominio frecuencia) causa rizados en el dominio de tiempo. En cada caso, la transformada de Fourier de la función rectangular es la función sinc.
Hay artefactos causados por otros efectos del dominio de frecuencia y artefactos similares pueden estar motivados por causas sin relación aparente.
Causas[editar]
Descripción[editar]


Por definición, el anillamiento ocurre cuando una entrada no oscilante produce una salida oscilante: formalmente, cuando una señal de entrada monótona en un intervalo tiene una respuesta de salida no monótona. Esto ocurre más a menudo cuando la respuesta a impulso o la respuesta de paso de un filtro oscila.
El anillamiento está íntimamente relacionado con el rebasamiento superior e inferior, que sucede cuando la salida toma valores por encima o por debajo del valor de entrada máximo y mínimo. Puede existir uno sin el otro, pero en casos importantes como con un filtro pasa bajo, primero hay un rebasamiento por encima, luego la respuesta rebota, cae y se estabiliza causando el primer anillo. Luego oscila por debajo del nivel estable. Por lo tanto, el rebasamiento superior es el primer paso del fenómeno, mientras que el anillamiento es el segundo paso. Debido a esta conexión, los términos se vinculan con frecuencia con "anillamiento".
Si se tiene un filtro LTI, entonces se puede entender el filtro y el anillamiento en términos de respuesta a impulso (vista de dominio de tiempo), o en términos de su transformada de Fourier, la respuesta en frecuencia (vista de dominio de frecuencia). El anillamiento es un artefacto de dominio de tiempo, y en diseño de filtro se compensa con las características de dominio de frecuencia deseadas: la respuesta de frecuencia deseada puede causar anillamiento mientras que reducir o eliminar el anillamiento puede empeorar la respuesta de frecuencia.
Filtro sinc[editar]
Artículo principal: Filtro Sinc

El ejemplo central, y a menudo referido como "artefactos de anillo", es el filtro pasa bajo ideal, el filtro sinc. Esto es una función de respuesta a impulso oscilatorio, como se ilustra arriba, y la respuesta de paso – su integral (seno integral) – así como oscilaciones de características, como se ilustra a la derecha.
Estos artefactos de anillo son el resultado de una implementación imperfecta: el filtro pasa bajo ideal, mientras posea la respuesta de frecuencia deseada, necesariamente causa artefactos en el dominio tiempo.
Dominio de tiempo[editar]
En términos de respuesta de impulso, la correspondencia entre estos artefactos y el comportamiento de la función es como sigue:
- el impulso de rebasamiento inferior equivale a la respuesta de impulso que tiene valores negativos,
- el anillamiento de impulso (anillamiento cerca de un punto) es equivalente a la respuesta de impulso que oscila, la cual es equivalente a la derivada de la respuesta de impulso que alterna entre valores negativos y positivos,
- no hay noción de rebasamiento por encima de impulso, ya que se asume que la unidad de impulso tiene una altura infinita así que no se puede rebasar.
La respuesta de paso, es la integral de la respuesta a impulso. Formalmente, el valor de la respuesta de paso en el momento a es la integral de la respuesta a impulso. Así que los valores de la respuesta de paso pueden entenderse en términos de cola de integrales de respuesta a impulso.
Asumir que la integral de la respuesta a impulso es 1, así que envía una entrada constante a la misma constante como salida – de otra forma, el filtro tiene ganancia, y escalando por ganancia se obtiene una integral de 1.
- El paso por rebasamiento inferior es equivalente a una cola integral negativa, en cuyo caso, la magnitud del rebasamiento es el de la cola integral.
- El paso por rebasamiento superior es equivalente a una cola integral mayor de 1, en cuyo caso, la magnitud del rebasamiento es la cantidad por la que la cola integral excede de 1 – o el valor de la cola en otra dirección,
- El paso del anillamiento es equivalente a la cola de integrales alternando entre valores crecientes y decrecientes – esto equivale a la respuesta a impulso alternando entre valores positivos y negativos.[3] Las regiones donde la respuesta a impulso están por debajo o por encima del eje x (formalmente, regiones entre ceros) se llaman lóbulos y la magnitud de una oscilación (desde el pico hasta la base) iguala la integral del lóbulo correspondiente.
La respuesta a impulso puede tener muchos lóbulos negativos, y por ello, muchas oscilaciones, generando un anillo que decae con filtros prácticos, por lo que generalmente solo se ven pocos anillos, siendo el primero el más pronunciado.
Nótese que si la respuesta a impulso tiene pequeños lóbulos negativos y mayores lóbulos positivos, entonces mostrará anillamiento pero sin rebasar superior e inferiormente. La cola integral siempre estará entre 0 y 1, pero oscilará hacia abajo en cada lóbulo negativo. Sin embargo, en el filtro sinc, los lóbulos decaen en magnitud y alternan en signo y en la serie armónica. La cola de integrales alterna en signo también, mostrando el rebasamiento superior como anillamiento.
Inversamente, si la respuesta a impulso es siempre positiva, es decir, que no tiene lóbulos negativos – la función es una distribución de la probabilidad – entonces la respuesta de paso no mostrará ni anillamiento ni rebasamiento superior o inferior – será una función monotónica creciendo de 0 a 1 como una función de distribución acumulativa. Así que la solución básica desde la perspectiva de dominio de tiempo es utilizar filtros con una respuesta a impulso positiva.
Dominio de frecuencia[editar]
La perspectiva de dominio de frecuencia es que el anillamiento está causado por el corte limpio en el pasabanda rectangular del dominio de frecuencia.[1][4]
Soluciones[editar]
Las soluciones dependen de los parámetros del problema: si la causa es un filtro pasa bajo, se puede elegir un diseño de filtro diferente que reduzca los artefactos a expensas de un peor rendimiento del dominio de frecuencia. Por otro lado, si la causa es una señal con límite de banda, como en JPEG, no se puede reemplazar simplemente el filtro y los artefactos de anillo pueden ser difíciles de arreglar – están presentes en JPEG 2000 y en muchos codecs de compresión de audio (en la forma de pre-eco).
Filtro pasa bajo[editar]

Si la causa es el uso de un filtro pasa bajo, se puede reemplazar el filtro con uno que reduzca los artefactos en el dominio tiempo, empeorando el rendimiento del dominio de frecuencia. Esto se puede analizar desde el dominio de tiempo o la perspectiva de dominio de frecuencia.
En el dominio de tiempo. la causa es una respuesta a impulso que oscila, asumiendo valores negativos. Esto se puede resolver utilizando un filtro cuya respuesta a impulso es no negativa y no oscilante, pero comparte los rasgos deseados. Por ejemplo, para un filtro pasa bajo, el filtro gaussiano es no negativo y no oscilante, así que no causa anillamiento. Sin embargo, no es tan bueno como el filtro pasa bajo. En términos de imagen, un filtro gaussiano "desenfoca" la señal, que refleja la atenuación de las señales de frecuencia más altas.
Una solución general es utilizar una función de ventana en el filtro sinc, que corta o reduce los lóbulos negativos. Estos eliminan y reducen respectivamente el rebasamiento superior y el anillamiento. Nótese que truncar algunos pero no todos los lóbulos elimina el anillamiento más allá de ese punto, pero no reduce la amplitud del anillamiento que no está truncado (porque está se determina por el tamaño del lóbulo), e incrementa la magnitud del rebasamiento superior si el último lóbulo no cortado es negativo,ya que la magnitud del rebasamiento superior es la integral de la cola, que no es cancelada por lóbulos positivos.
En implementaciones prácticas, uno al menos trunca sinc, de lo contrario debe usar muchos puntos infinitamente (o todos los puntos de la señal) para calcular cada punto de la salida – el truncado corresponde a una ventana rectangular, y hace que el filtro sea posible de implementar, pero la respuesta de frecuencia ya no es perfecta.[5]
De hecho, si se toma un filtro pasa bajo (sinc en dominio de tiempo, rectangular en dominio de frecuencia) y se trunca (se multiplica con una función rectangular en el dominio de tiempo), esto convoluciona el dominio de frecuencia con sinc (transformada de Fourier de la función rectangular) y causa anillamiento en el dominio de frecuencia,[2] el cual se denomina rizado. En símbolos,
La multiplicación en el dominio tiempo corresponde a la convolución en el dominio frecuencia, así que multiplicar un filtro por una función de ventana corresponde a convolucionar la transformada de Fourier del filtro original por la transformada de Fourier de la ventana, la cual tiene un efecto más suave – así que aplicar la ventana en el dominio tiempo corresponde al suavizado en el dominio frecuencia, y reduce o elimina el rebasamiento y el anillamiento.[6]
En el dominio de la frecuencia, la causa se puede interpretar como debido al corte limpio y el anillamiento reducido por usar un filtro.[1] Este es el caso del filtro gaussiano cuya magnitud en el diagrama de Bode es una parábola abierta descendente. Como su transformada de Fourier es gaussiana, – tomando los logaritmos se genera
Beneficios[editar]

Aunque los artefactos de anillo normalmente se consideran indeseables, el rebasamiento superior inicial en las transiciones incrementa la acutancia (nitidez aparente) incrementando la derivativa sobre la transición y así puede considerarse como una mejora.[7]
Fenómenos relacionados[editar]
Rebasamiento por encima[editar]


Otro artefacto es el rebasamiento superior (e inferior), que se manifiesta no como anillos sino como un salto incrementado en la transición. Está relacionado con el anillamiento y, a menudo, ocurre en combinación con ello.
El rebasamiento superior e inferior está causado por una cola negativa – en la función sinc, la integral del primer cero a infinito, incluye el primer lóbulo negativo mientras que el anillado está causado por una cola positiva – en sinc, la integral desde el segundo cero a infinito, incluye el primer lóbulo positivo no central. Así que el rebasamiento superior es necesario para el anillamiento, pero puede ocurrir de forma separada: por ejemplo, el filtro Lanczos tiene solo un lóbulo negativo en cada lado, sin lóbulos positivos que le sucedan, y eso muestra un rebasamiento superior pero sin anillamiento, mientras que el filtro Lanczos de tres lóbulos muestra tanto rebasamiento como anillamiento, aunque la ventana reduce esto comparado con el filtro sinc.
Recorte[editar]
Tras el rebasamiento por encima y por debajo, está el recorte. Si la señal está limitada, por ejemplo a un entero de 8 o 16 bits, el rebasamiento puede exceder el rango de valores permitidos, causando recorte.
Hablando estrictamente, el recorte está causado por la combinación del rebasamiento por encima y la exactitud numérica limitada, pero muy asociada al anillamiento y a menudo, este ocurre cuando se combinan.
El recorte puede ocurrir por razones que no guardan relación, por una señal que simplemente excede el rango de un canal.
Anillamiento y rizado[editar]
En procesamiento de señal y campos relacionados, al fenómeno general de oscilación de dominio de tiempo se le llama anillamiento mientras que a las oscilaciones en dominio de frecuencia se les llama rizado.
La fuente principal del rizado en el procesado de señal digital es el uso de funciones ventana. Tomando un filtro de respuesta infinita al impulso, como el filtro sinc, y aplicando una función ventana para que tenga una respuesta finita al impulso, como en el método de diseño de ventana, entonces la respuesta de frecuencia del filtro resultante es la convolución de la respuesta de frecuencia del filtro IIR con la respuesta de frecuencia de la función ventana. La respuesta de frecuencia del filtro rectangular es la función sinc (la función rectangular y la función sinc son variables duales Fourier respectivamente), así que truncar un filtro en el dominio de tiempo corresponde a la multiplicación por el filtro rectangular. Así, la convolución con el filtro sinc en el dominio de frecuencia causa rizado. En símbolos, la respuesta de frecuencia de es En particular, truncar la función sinc genera en el dominio tiempo, y en el dominio frecuencia, así que como filtro pasa bajo (truncando en el dominio frecuencia) se causa anillamiento en el dominio tiempo, truncando en el dominio tiempo (aplicando una función ventana con un filtro rectangular) se causa rizado en el dominio frecuencia.
Ejemplos[editar]
JPEG[editar]


La compresión JPEG puede introducir artefactos de anillo en transiciones claras que son particularmente visibles en el texto.
Se debe a la pérdida de componentes de alta frecuencia, como en los anillamientos de respuesta de paso. JPEG usa bloques de 8×8, en los cuales se realiza la transformada de coseno discreta (DCT). DCT es una transformada de Fourier relacionada, y el anillamiento ocurre debido a la pérdida de componentes de alta frecuencia o pérdida de precisión en los componentes de alta frecuencia.
También pueden ocurrir en el borde de una imagen: como JPEG trocea las imágenes en bloques de 8×8, si una imagen no tiene un número entero de bloques, el borde no se puede codificar fácilmente, y las soluciones como el relleno con un borde negro crea una transición clara en la fuente. De ahí los artefactos de anillo en la imagen codificada.
El anillamiento también ocurre en el formato JPEG 2000 basado en óndula.
JPEG y JPEG 2000 tienen otros artefactos, como los ilustrados arriba, tales como el ruido de mosquito, aunque estos se deben a peculiaridades de los formatos y no se discuten aquí.
Algunas ilustraciones:
| Imagen | Compresión sin pérdida | Compresión con pérdida |
|---|---|---|
| Original |  |

|
| Procesado por Algoritmo de Canny, artefactos brillantes. |
 |

|
Pre-eco[editar]

En procesamiento digital de audio, el anillamiento causa ecos que ocurren antes y después de las transiciones, como el sonido impulsivo de un instrumento de percusión como los platillos (esto es anillamiento por impulso). El eco después de la transición no se oye porque está enmascarado por la transición, un efecto denominado enmascaramiento temporal. Como solo el eco anterior a la transición se puede escuchar, el fenómeno se llama pre-eco.
Este fenómeno ocurre como un artefacto de compresión en algoritmos de compresión de audio que utilizan transformadas de Fourier relacionadas, como MP3, AAC, y Vorbis.
Fenómeno similar[editar]
Otros fenómenos tienen síntomas similares al anillamiento, pero sus causas son distintas.
Mejora de borde[editar]
La mejora de borde, que incrementa los bordes, puede causar el fenómeno de anillamiento, particularmente bajo una aplicación repetida, como un reproductor DVD seguido por una televisión. Esto puede hacerse con un filtro pasa alto, más que con uno pasa bajo.[4]
Funciones especiales[editar]
Muchas funciones especiales muestran un decaimiento oscilatorio, produciendo anillamiento en la salida. Puede tenerse en consideración estos anillamientos o restringir el término a artefactos no intencionados en el procesamiento de la señal de dominio de frecuencia.
La difracción de Fraunhofer produce el disco de Airy como la función del punto expandido, la cual tiene patrón de anillamiento.

La función de Bessel de primer tipo, la cual está relacionada con la función de Airy, muestra tal decaimiento.

En las cámaras, una combinación de desenfoque y aberración esférica puede dar lugar a patrones de anillo.
Interferencia[editar]
Ghosting es una forma de interferencia de televisión donde una imagen se repite. Aunque esto no es anillamiento, puede interpretarse como una circunvolución con una función que es 1 en origen y ε (la intensidad del fantasma) a alguna distancia, lo cual es formalmente similar a las funciones citadas.
Brillo de lente[editar]
En fotografía, el brillo de lente es un defecto donde pueden aparecer varios círculos alrededor de reflejos, y con "fantasmas" sobre la foto, debido a luz no deseada, reflejos y dispersiones de los elementos en la lente.
Ilusiones visuales[editar]

En las transiciones pueden ocurrir ilusiones visuales, como en las Bandas de Mach, en las cuales se muestra un rebasamiento por encima y por debajo similar al del fenómeno Gibbs.
Véase también[editar]
- Artefacto (error de observación)
- Filtro Sinc
- Aberración cromática
- Ghosting (televisión)
- Fenómeno de Gibbs
- Filtro pasa bajo
- Pre-eco
Referencias[editar]
- ↑ a b c Bankman, Isaac N. (2000), Handbook of medical imaging, Academic Press, ISBN 978 0 12077790 7., section I.6, Enhancement: Frequency Domain Techniques, p. 16
- ↑ a b Digital Signal Processing, by J.S.Chitode, Technical Publications, 2008, ISBN 978 8 18431346 8, 4 - 70
- ↑ Glassner, Andrew S (2004), Principles of Digital Image Synthesis (2 edición), Morgan Kaufmann, ISBN 978 1 55860276 2., p. 518
- ↑ a b Microscope Image Processing, by Qiang Wu, Fatima Merchant, Kenneth Castleman, ISBN 978 0 12372578 3 p. 71
- ↑ (Allen y Mills, 2004) Section 9.3.1.1 Ideal Filters: Low pass, p. 621
- ↑ (Allen y Mills, 2004) p. 623
- ↑ Mitchell, Don P.; Netravali, Arun N. (August de 1988). Reconstruction filters in computer-graphics. ACM SIGGRAPH International Conference on Computer Graphics and Interactive Techniques 22 (4). pp. 221-228. ISBN 0-89791-275-6. doi:10.1145/54852.378514.
- Allen, Ronald L.; Mills, Duncan W. (2004), Signal analysis: time, frequency, scale, and structure, Wiley-IEEE, ISBN 978 0 47123441 8.










