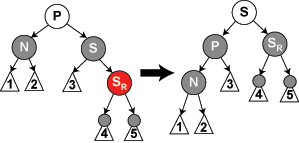
Árbol rojo-negro
Un árbol rojo-negro es un árbol binario de búsqueda equilibrado, una estructura de datos utilizada en informática y ciencias de la computación. La estructura original fue creada por Rudolf Bayer en 1972, que le dio el nombre de “árboles-B binarios simétricos”, pero tomó su nombre moderno en un trabajo deLeo J. Guibas y Robert Sedgewick realizado en 1978. Es complejo, pero tiene un buen peor caso de tiempo de ejecución para sus operaciones y es eficiente en la práctica. Puede buscar, insertar y borrar en un tiempo O(log n), donde n es el número de elementos del árbol.
Terminología
[editar]Un árbol rojo-negro es un tipo especial de árbol binario usado en informática para organizar información compuesta por datos comparables (por ejemplo, números). En los árboles rojo-negro las hojas no son relevantes y no contienen datos.
En los árboles rojo-negro, como en todos los árboles binarios de búsqueda, es posible moverse ordenadamente a través de los elementos de forma eficiente si hay forma de localizar el padre de cualquier nodo. El tiempo de desplazarse desde la raíz hasta una hoja a través de un árbol equilibrado que tiene la mínima altura posible es de O(log n).
Al implementar esta estructura es posible utilizar un único nodo centinela. Este cumple la función de hoja para todas las ramas del árbol. Así, todos los nodos internos que finalicen en una hoja tienen referencia a este único nodo centinela. Esto no es necesario, ya que puede hacerse una referencia nula (NIL) en el final de cada rama.
Propiedades
[editar]
Un árbol rojo-negro es un árbol binario de búsqueda en el que cada nodo tiene un atributo de color cuyo valor es rojo o negro. En adelante, se dice que un nodo es rojo o negro haciendo referencia a dicho atributo.
Además de los requisitos impuestos a los árboles binarios de búsqueda convencionales, se deben satisfacer las siguientes reglas para tener un árbol rojo-negro válido:
- Todo nodo es o bien rojo o bien negro.
- La raíz es negra.
- Todas las hojas (NULL) son negras.
- Todo nodo rojo debe tener dos nodos hijos negros.
- Cada camino desde un nodo dado a sus hojas descendientes contiene el mismo número de nodos negros.
Estas reglas producen una regla crucial para los árboles rojo-negro: el camino más largo desde la raíz hasta una hoja no es más largo que dos veces el camino más corto desde la raíz a una hoja. El resultado es que dicho árbol está aproximadamente equilibrado.
Dado que las operaciones básicas como insertar, borrar y encontrar valores tienen un peor tiempo de ejecución proporcional a la altura del árbol, esta cota superior de la altura permite a los árboles rojo-negro ser eficientes en el peor caso, a diferencia de los árboles binarios de búsqueda.
Para comprobarlo basta ver que ningún camino puede tener dos nodos rojos seguidos debido a la propiedad 4. El camino más corto posible tiene todos sus nodos negros, y el más largo alterna entre nodos rojos y negros. Dado que todos los caminos máximos tienen el mismo número de nodos negros por la propiedad 5, no hay ningún camino que pueda tener longitud mayor que el doble de la longitud de otro camino.
En muchas presentaciones de estructuras arbóreas de datos, es posible para un nodo tener solo un hijo y las hojas contienen información. Es posible presentar los árboles rojo-negro en este paradigma, pero cambian algunas de las propiedades y se complican los algoritmos. Por esta razón, este artículo utiliza “hojas nulas”.
Una variante que se da al árbol rojo-negro es la de tratarlo como un árbol binario de búsqueda cuyas aristas, en lugar de nodos, son coloreadas de color rojo o negro, pero esto no produce ninguna diferencia. El color de cada nodo en la terminología de este artículo corresponde al color de la arista que une el nodo a su padre, excepto la raíz, que es siempre negra (por la propiedad 2) donde la correspondiente arista no existe.
Al número de nodos negros de un camino se le denomina "altura negra".
Usos y ventajas
[editar]Los árboles rojo-negro ofrecen un peor caso con tiempo garantizado para la inserción, el borrado y la búsqueda. No es esto únicamente lo que los hace valiosos en aplicaciones sensibles al tiempo como las aplicaciones en tiempo real, sino que además son apreciados para la construcción de bloques en otras estructuras de datos que garantizan un peor caso. Por ejemplo, muchas estructuras de datos usadas en geometría computacional pueden basarse en árboles rojo-negro.
El árbol AVL es otro tipo de estructura con O(log n) tiempo de búsqueda, inserción y borrado. Está equilibrado de forma más rígida que los árboles rojo-negro, lo que provoca que la inserción y el borrado sean más lentos pero la búsqueda y la devolución del resultado de la misma más veloz.
Los árboles rojo-negro son particularmente valiosos en programación funcional, donde son una de las estructuras de datos persistentes más comúnmente utilizadas en la construcción de arrays asociativos y conjuntos que pueden retener versiones previas tras mutaciones. La versión persistente del árbol rojo-negro requiere un espacio O(log n) para cada inserción o borrado, además del tiempo.
Los árboles rojo-negro son isométricos a los árboles 2-3-4. En otras palabras, para cada árbol 2-3-4, existe un árbol correspondiente rojo-negro con los datos en el mismo orden. La inserción y el borrado en árboles 2-3-4 son también equivalentes a los cambios de colores y las rotaciones en los árboles rojo-negro. Esto los hace ser una herramienta útil para la comprensión del funcionamiento de los árboles rojo-negro y por esto muchos textos introductorios sobre algoritmos presentan los árboles 2-3-4 justo antes que los árboles rojo-negro, aunque frecuentemente no sean utilizados en la práctica.
Operaciones
[editar]Las operaciones de sólo lectura en un árbol rojo-negro no requieren modificación alguna con respecto a las utilizadas en los árboles binarios de búsqueda, ya que cada árbol rojo-negro es un caso especial de árbol binario de búsqueda.
Sin embargo, el resultado inmediato de una inserción o la eliminación de un nodo utilizando los algoritmos de un árbol binario de búsqueda normal podría violar las propiedades de un árbol rojo-negro. Restaurar las propiedades rojo-negro requiere un pequeño número (O(log n))de cambios de color (que son muy rápidos en la práctica) y no más de 3 rotaciones (2 por inserción). A pesar de que las operaciones de inserción y borrado son complicadas, sus tiempos de ejecución siguen siendo O(log n).
Rotación
[editar]Para conservar las propiedades que debe cumplir todo árbol rojo-negro, en ciertos casos de la inserción y la eliminación será necesario reestructurar el árbol, si bien no debe perderse la ordenación relativa de los nodos. Para ello, se llevan a cabo una o varias rotaciones, que no son más que reestructuraciones en las relaciones padre-hijo-tío-nieto.
Las rotaciones que se consideran a continuación son simples; sin embargo, también se dan las rotaciones dobles.
En las imágenes pueden verse de forma simplificada cómo se llevan a cabo las rotaciones simples hacia la izquierda y hacia la derecha en cualquier árbol binario de búsqueda, en particular en cualquier árbol rojo-negro. Podemos ver también la implementación en Python de dichas operaciones.
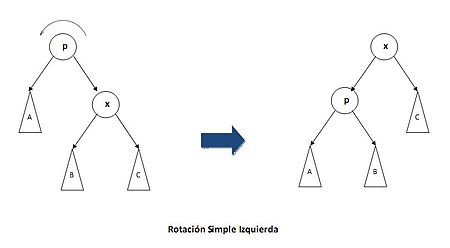
def rotar_izda(p):
aux = raiz
if p.padre is not None and p.padre.dcho == p:
aux = p.padre.dcho
elif p.padre is not None and p.padre.izdo == p:
aux = p.padre.izdo
aux = p.dcho
aux.padre = p.padre
p.padre = aux
p.dcho = aux.izdo
aux.izdo = p
if p.dcho is not None:
p.dcho.padre = p

def rotar_dcha(p):
aux = None
if p.padre is not None and p.padre.dcho == p:
aux = p.padre.dcho
elif p.padre is not None and p.padre.izdo == p:
aux = p.padre.izdo
aux = p.izdo
aux.padre = p.padre
p.padre = aux
p.izdo = aux.dcho
aux.dcho = p
if p.izdo is not None:
p.izdo.padre = p
Búsqueda
[editar]La búsqueda consiste acceder a la raíz del árbol y comparar su valor con el valor buscado. Si el elemento a localizar coincide con el de la raíz, la búsqueda ha concluido con éxito. Si el elemento es menor, se busca en el subárbol izquierdo; si es mayor, en el derecho. Si se alcanza un nodo hoja y el elemento no ha sido encontrado se supone que no existe en el árbol. Cabe destacar que la búsqueda en este tipo de árboles es muy eficiente y representa una función logarítmica. La búsqueda de un elemento en un ABB (Árbol Binario de Búsqueda) en general, y en un árbol rojo-negro en particular, se puede realizar de dos formas: iterativa y recursiva.
Ejemplo de versión iterativa en el lenguaje de programación Python, suponiendo que estamos buscando una clave alojada en un nodo donde está el correspondiente dato que precisamos encontrar:
def buscar_abb_iterativo(a, buscado):
e = None
p = a
while p is not None and p.valor != buscado:
# avanzar el puntero
if buscado < p.valor:
p = p.izquierda
if p.valor < buscado:
p = p.derecha
if p is not None:
e = copiaDato(p.dato)
return e
}
Véase ahora la versión recursiva en ese mismo lenguaje:
def buscar_abb_recursivo(a, buscado):
if a is None:
return None
if a.valor == buscado:
return copiaDato(a.valor)
if a.valor < buscado:
return buscar_abb_recursivo(a.derecha, buscado)
if a.valor > buscado:
return buscar_abb_recursivo(a.izquierda, buscado)
Inserción
[editar]La inserción comienza añadiendo el nodo como lo haríamos en un árbol binario de búsqueda convencional y pintándolo de rojo. Lo que sucede después depende del color de otros nodos cercanos. El término tío nodo será usado para referenciar al hermano del padre de un nodo, como en los árboles familiares humanos. Conviene notar que:
- La propiedad 3 (Todas las hojas nulas, son negras) siempre se cumple.
- La propiedad 4 (Ambos hijos de cada nodo rojo son negros) está amenazada solo por añadir un nodo rojo, por repintar un nodo negro de color rojo o por una rotación.
- La propiedad 5 (Todos los caminos desde un nodo dado hasta sus nodos hojas contiene el mismo número de nodos negros) está amenazada solo por repintar un nodo negro de color rojo o por una rotación.
Al contrario de lo que sucede en otros árboles como puede ser el Árbol AVL, en cada inserción se realiza un máximo de una rotación, ya sea simple o doble. Por otra parte, se asegura un tiempo de recoloración máximo de por cada inserción.
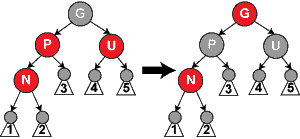
- Nota: En los esquemas que acompañan a los algoritmos, la etiqueta N será utilizada por el nodo que está siendo insertado, P para los padres del nodo N, G para los abuelos del nodo N, y U para los tíos del nodo N. Notamos que los roles y etiquetas de los nodos están intercambiados entre algunos casos, pero en cada caso, toda etiqueta continúa representando el mismo nodo que representaba al comienzo del caso. Cualquier color mostrado en el diagrama está o bien supuesto en el caso o implicado por dichas suposiciones.
Los nodos tío y abuelo pueden ser encontrados por las siguientes funciones:
struct node *
abuelo(struct node *n)
{
if ((n != NULL) && (n->padre != NULL))
return n->padre->padre;
else
return NULL;
}
struct node *
tio(struct node *n)
{
struct node *a = abuelo(n);
if (n->padre == a->izdo)
return a->dcho;
else
return a->izdo;
}
Estudiemos ahora cada caso de entre los posibles que nos podemos encontrar al insertar un nuevo nodo.
Caso 1: El nuevo nodo N es la raíz del árbol. En este caso, es repintado en color negro para satisfacer la propiedad 2 (la raíz es negra). Como esto añade un nodo negro a cada camino, la propiedad 5 (todos los caminos desde un nodo dado a sus hojas contiene el mismo número de nodos negros) se mantiene. En C quedaría así:
void
insercion_caso1(struct node *n)
{
if (n->padre == NULL)
n->color = NEGRO;
else
insercion_caso2(n);
}
Caso 2: El padre del nuevo nodo (esto es, el nodo P) es negro, así que la propiedad 4 (ambos hijos de cada nodo rojo son negros) se mantiene. En este caso, el árbol es aun válido. La propiedad 5 (todos los caminos desde cualquier nodo dado a sus hojas contiene igual número de nodos negros) se mantiene, porque el nuevo nodo N tiene dos hojas negras como hijos, pero como N es rojo, los caminos a través de cada uno de sus hijos tienen el mismo número de nodos negros que el camino hasta la hoja que reemplazó, que era negra, y así esta propiedad se mantiene satisfecha. Su implementación:
void
insercion_caso2(struct node *n)
{
if (n->padre->color == NEGRO)
return; /* Árbol válido. */
else
insercion_caso3(n);
}
- Nota: En los siguientes casos se puede asumir que N tiene un abuelo, el nodo G, porque su padre P es rojo, y si fuese la raíz, sería negro. Consecuentemente, N tiene también un nodo tío U a pesar de que podría ser una hoja en los casos 4 y 5.
void
insercion_caso3(struct node *n)
{
struct node *t = tio(n), *a;
if ((t != NULL) && (t->color == ROJO)) {
n->padre->color = NEGRO;
t->color = NEGRO;
a = abuelo(n);
a->color = ROJO;
insercion_caso1(a);
} else {
insercion_caso4(n);
}
}
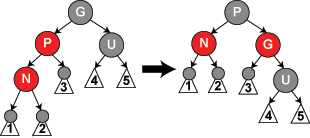
- Nota: En los casos restantes, se asume que el nodo padre P es el hijo izquierdo de su padre. Si es el hijo derecho, izquierda y derecha deberían ser invertidas a partir de los casos 4 y 5. El código del ejemplo toma esto en consideración.
void
insercion_caso4(struct node *n)
{
struct node *a = abuelo(n);
if ((n == n->padre->dcho) && (n->padre == a->izdo)) {
rotar_izda(n->padre);
n=n->izdo;
} else if ((n == n->padre->izdo) && (n->padre == a->dcho)) {
rotar_dcha(n->padre);
n=n->dcho;
}
insercion_caso5(n);
}
void
insercion_caso5(struct node *n)
{
struct node *a = abuelo(n);
n->padre->color = NEGRO;
a->color = ROJO;
if ((n == n->padre->izdo) && (n->padre == a->izdo)) {
rotar_dcha(a);
} else {
/*
* En este caso, (n == n->padre->dcho) && (n->padre == a->dcho).
*/
rotar_izda(a);
}
}
- Nótese que la inserción se realiza sobre el propio árbol y que los códigos del ejemplo utilizan recursión de cola.
Eliminación
[editar]En un árbol binario de búsqueda normal, cuando se borra un nodo con dos nodos internos como hijos, tomamos el máximo elemento del subárbol izquierdo o el mínimo del subárbol derecho, y movemos su valor al nodo que es borrado (como se muestra aquí). Borramos entonces el nodo del que copiábamos el valor que debe tener menos de dos nodos no hojas por hijos. Copiar un valor no viola ninguna de las propiedades rojo-negro y reduce el problema de borrar en general al de borrar un nodo con como mucho un hijo no hoja. No importa si este nodo es el nodo que queríamos originalmente borrar o el nodo del que copiamos el valor.
Resumiendo, podemos asumir que borramos un nodo con como mucho un hijo no hoja (si solo tiene nodos hojas por hijos, tomaremos uno de ellos como su hijo). Si borramos un nodo rojo, podemos simplemente reemplazarlo con su hijo, que debe ser negro. Todos los caminos hasta el nodo borrado simplemente pasarán a través de un nodo rojo menos, y ambos nodos, el padre del borrado y el hijo, han de ser negros, así que las propiedades 3 (todas las hojas, incluyendo las nulas, son negras) y 4 (los dos hijos de cada nodo rojo son negros) se mantienen. Otro caso simple es cuando el nodo borrado es negro y su hijo es rojo. Simplemente eliminar un nodo negro podría romper las propiedades 4 (los dos hijos de cada nodo rojo son negros) y 5 (todos los caminos desde un nodo dado hasta sus hojas contienen el mismo número de nodos negros), pero si repintamos su hijo de negro, ambas propiedades quedan preservadas.
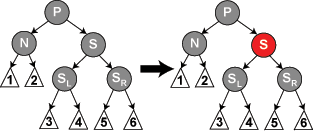
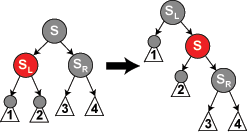
El caso complejo es cuando el nodo que va a ser borrado y su hijo son negros. Empezamos por reemplazar el nodo que va a ser borrado con su hijo. Llamaremos a este hijo (en su nueva posición) N, y su hermano (el otro hijo de su nuevo padre) S. En los diagramas de debajo, usaremos P para el nuevo padre de N, SL para el hijo izquierdo de S, y SR para el nuevo hijo derecho de S (se puede mostrar que S no puede ser una hoja).
- Nota: Entre algunos casos cambiamos roles y etiquetas de los nodos, pero en cada caso, toda etiqueta sigue representando al mismo nodo que representaba al comienzo del caso. Cualquier color mostrado en el diagrama es o bien supuesto en su caso o bien implicado por dichas suposiciones. El blanco representa un color desconocido (o bien rojo o bien negro).
El cumplimiento de estas reglas en un árbol con n nodos, asegura un máximo de tres rotaciones y hasta recoloraciones.
Encontraremos el hermano usando esta función:
struct node *
hermano(struct node *n)
{
if (n == n->padre->izdo)
return n->padre->dcho;
else
return n->padre->izdo;
}
- Nota: Con el fin de preservar la buena definición del árbol, necesitamos que toda hoja nula siga siendo una hoja nula tras todas las transformaciones (que toda hoja nula no tendrá ningún hijo). Si el nodo que estamos borrando tiene un hijo no hoja N es fácil ver que la propiedad se satisface. Si, por otra parte N fuese una hoja nula, se verifica por los diagramas o el código que para todos los casos la propiedad se satisface también.
Podemos realizar los pasos resaltados arriba con el siguiente código, donde la función reemplazar_nodo sustituye hijo en el lugar de n en el árbol. Por facilitar la comprensión del ejemplo, en el código de esta sección supondremos que las hojas nulas están representadas por nodos reales en lugar de NULL (el código de la sección inserción trabaja con ambas representaciones).
void
elimina_un_hijo(struct node *n)
{
/*
* Precondición: n tiene al menos un hijo no nulo.
*/
struct node *hijo = es_hoja(n->dcho) ? n->izdo : n->dcho;
reemplazar_nodo(n, hijo);
if (n->color == NEGRO) {
if (hijo->color == ROJO)
hijo->color = NEGRO;
else
eliminar_caso1(hijo);
}
free(n);
}
- Nota: Si N es una hoja nula y no queremos representar hojas nulas como nodos reales, podemos modificar el algoritmo llamando primero a eliminar_caso1() en su padre (el nodo que borramos, n en el código anterior) y borrándolo después. Podemos hacer esto porque el padre es negro, así que se comporta de la misma forma que una hoja nula (y a veces es llamada hoja “fantasma”). Y podemos borrarla con seguridad, de tal forma que n seguirá siendo una hoja tras todas las operaciones, como se muestra arriba.
Si N y su padre original son negros, entonces borrar este padre original causa caminos que pasan por N y tienen un nodo negro menos que los caminos que no. Como esto viola la propiedad 5 (todos los caminos desde un nodo dado hasta su nodos hojas deben contener el mismo número de nodos negros), el árbol debe ser reequilibrado. Hay varios casos a considerar.
Caso 1: N es la nueva raíz. En este caso, hemos acabado. Borramos un nodo negro de cada camino y la nueva raíz es negra, así las propiedades se cumplen. Una posible implementación en el lenguaje de programación C sería la siguiente:
void
eliminar_caso1(struct node *n)
{
if (n->padre!= NULL)
eliminar_caso2(n);
}
- Nota: En los casos 2, 5 y 6, asumimos que N es el hijo izquierdo de su padre P. Si este fuese el hijo derecho, la izquierda y la derecha deberían ser invertidas en todos estos casos. De nuevo, el código del ejemplo toma ambos casos en cuenta.
void
eliminar_caso2(struct node *n)
{
struct node *hm = hermano(n);
if (hm->color == ROJO) {
n->padre->color = ROJO;
hm->color = NEGRO;
if (n == n->padre->izdo)
rotar_izda(n->padre);
else
rotar_dcha(n->padre);
}
eliminar_caso3(n);
}
void
eliminar_caso3(struct node *n)
{
struct node *hm = hermano_menor(n);
if ((n->padre->color == NEGRO) &&
(hm->color == NEGRO) &&
(hm->izdo->color == NEGRO) &&
(hm->dcho->color == NEGRO)) {
hm->color = ROJO;
eliminar_caso1(n->padre);
} else
eliminar_caso4(n);
}
void
eliminar_caso4(struct node *n)
{
struct node *hm = hermano_menor(n);
if ((n->padre->color == ROJO) &&
(hm->color == NEGRO) &&
(hm->izdo->color == NEGRO) &&
(hm->dcho->color == NEGRO)) {
hm->color = ROJO;
n->padre->color = NEGRO;
} else
eliminar_caso5(n);
}
void
eliminar_caso5(struct node *n)
{
struct node *hm = hermano(n);
if ((n == n->padre->izdo) &&
(hm->color == NEGRO) &&
(hm->izdo->color == ROJO) &&
(hm->dcho->color == NEGRO)) {
hm->color = ROJO;
hm->izdo->color = NEGRO;
rotar_dcha(hm);
} else if ((n == n->padre->dcho) &&
(hm->color == NEGRO) &&
(hm->dcho->color == ROJO) &&
(hm->izdo->color == NEGRO)) {
hm->color = ROJO;
hm->dcho->color = NEGRO;
rotar_izda(hm);
}
eliminar_caso6(n);
}
void
eliminar_caso6(struct node *n)
{
struct node *hm = hermano(n);
hm->color = n->padre->color;
n->padre->color = NEGRO;
if (n == n->padre->izdo) {
/*
* Aquí, hm->dcho->color == ROJO.
*/
hm->dcho->color = NEGRO;
rotar_izda(n->padre);
} else {
/*
* Aquí, hm->izdo->color == ROJO.
*/
hm->izdo->color = NEGRO;
rotar_dcha(n->padre);
}
}
De nuevo, todas las llamadas de la función usan recursión de cola así que el algoritmo realiza sus operaciones sobre el propio árbol. Además, las llamadas no recursivas se harán después de una rotación, luego se harán un número de rotaciones (más de 3) que será constante.
Demostración de cotas
[editar]Un árbol rojo-negro que contiene n nodos internos tiene una altura de O(log(n)).
Hagamos los siguientes apuntes sobre notación:
- H(v) = altura del árbol cuya raíz es el nodo v.
- bh(v) = número de nodos negros (sin contar v si es negro) desde v hasta cualquier hoja del subárbol (llamado altura-negra).
Lema: Un subárbol enraizado al nodo v tiene al menos nodos internos.
Demostración del lema (por inducción sobre la altura):
Caso base: h(v)=0 Si v tiene altura cero entonces debe ser árbol vacío, por tanto bh(v)=0. Luego:
Hipótesis de Inducción: si v es tal que h(v) = k y contiene nodos internos, veamos que esto implica que tal que h() = k+1 contiene nodos internos.
Si tiene h() > 0 entonces es un nodo interno. Como este tiene dos hijos que tienen altura-negra, o bh() o bh()-1 (dependiendo si es rojo o negro). Por la hipótesis de inducción cada hijo tiene al menos nodos internos, así que tiene : nodos internos.
Usando este lema podemos mostrar que la altura del árbol es algorítmica. Puesto que al menos la mitad de los nodos en cualquier camino desde la raíz hasta una hoja negra (propiedad 4 de un árbol rojo-negro), la altura-negra de la raíz es al menos h(raíz)/2. Por el lema tenemos que:
Por tanto, la altura de la raíz es O(log(n)).
Complejidad
[editar]En el código del árbol hay un bucle donde la raíz de la propiedad rojo-negro que hemos querido devolver a su lugar, x, puede ascender por el árbol un nivel en cada iteración Como la altura original del árbol es O(log n), hay O(log n) iteraciones. Así que en general la inserción tiene una complejidad de O(log n).
Véase también
[editar]- Lenguaje de especificación de TADs Maude
- Lista enlazada
- Pila
- Cola
- Conjunto
- Árbol binario
- Árbol binario de búsqueda
- Árbol AA
- Árbol AVL
- Árbol biselado
- Montículo
- Montículo binomial
- Montículo de Fibonacci
- Árbol 2-3
- Árbol 2-3-4
- Árbol-B
- Árbol splay
- Grafo
Bibliografía
[editar]- Hernández, Zenón; Rodríguez, J.Carlos; González, J.Daniel; Díaz, Margarita; Pérez, José; Rodríguez, Gustavo. (2005). Fundamentos de Estructuras de Datos. Soluciones en Ada, Java y C++. Madrid: Thomson Editores Spain. 84-9732-358-0.
- Weisstein, Eric W. «Red-Black Tree». En Weisstein, Eric W, ed. MathWorld (en inglés). Wolfram Research..
- San Diego State University: CS 660: Red-Black tree notes Archivado el 9 de mayo de 2008 en Wayback Machine., by Roger Whitney.
- Thomas H. Cormen, Charles E. Leiserson, Ronald L. Rivest, and Clifford Stein. Introduction to Algorithms, Second Edition. MIT Press and McGraw-Hill, 2001. ISBN 0-262-03293-7 . Chapter 13: Red-Black Trees, pp.273–301.
- Pfaff, Ben (junio de 2004). «Performance Analysis of BSTs in System Software» (PDF). Stanford University..
- Okasaki, Chris. «Red-Black Trees in a Functional Setting» (PS). Archivado desde el original el 26 de septiembre de 2007..
Enlaces externos
[editar]Demos y simuladores
[editar]- Simulador de árboles Rojo-Negro Archivado el 16 de junio de 2007 en Wayback Machine..
- Red Black Tree visualisation, una demo de los árboles rojo-negro y otros muchos más árboles de búsqueda, por Kubo Kovac.
- Red Black Tree Applet, una demo de los árboles rojo-negro, AVL, rotaciones y mucho más.
- Red/Black Tree Demonstration, una demo interactiva acerca de la inserción y eliminación con una implementación en Java.
- Red-Black Tree Animation, una demostración de la inserción en el peor caso.
- aiSee: Visualization of a Sorting Algorithm, GIF animado que muestra la inserción (200KB).
- Red-Black Tree Demonstration, una demo acerca de la inserción, en código Java, por David M. Howard.
Implementaciones
[editar]- Descargar Programa Red-black en java.
- En la librería de C++, Standard Template Library, los contenedores
std::set<Value>ystd::map<Key,Value>están implementados a menudo con árboles rojo-negro. - Implementación eficiente de árboles rojo-negro.
- RBT: Una biblioteca de árboles rojo-negro en SmallEiffel. Archivado el 7 de octubre de 2017 en Wayback Machine.
- libredblack: Una biblioteca de árboles rojo-negro en C.
- Código en C de árboles rojo-negro.
- Implementación en Java de os árboles rojo-negro en java.util.TreeMap
- Los subsistemas de DragonFlyBSD VM utilizan árboles rojo-negro.
- NATURAL/ADABAS implementación de Paul Macgowan
- NGenerics : implementación en C#
- FreeBSD's single header file implementation
- The default scheduler of Linux 2.6.23, called Completely Fair Scheduler, is implemented via a Red-Black tree