Árbol binario
En ciencias de la computación, un árbol binario es una estructura de datos en la cual cada nodo puede tener un hijo izquierdo y un hijo derecho. No pueden tener más de dos hijos (de ahí el nombre "binario"). Si algún hijo tiene como referencia a null, es decir que no almacena ningún dato, entonces este es llamado un nodo externo. En el caso contrario el hijo es llamado un nodo interno. Usos comunes de los árboles binarios son los árboles binarios de búsqueda, los montículos binarios y Codificación de Huffman.
Definición de teoría de grafos[editar]
En teoría de grafos, se usa la siguiente definición: «Un árbol binario es un grafo conexo, acíclico y no dirigido tal que el grado de cada vértice no es mayor a 2». De esta forma solo existe un camino entre un par de nodos.
Un árbol binario con enraizado es como un grafo que tiene uno de sus vértices, llamado raíz, de grado no mayor a 2. Con la raíz escogida, cada vértice tendrá un único padre, y nunca más de dos hijos. Si rehusamos el requerimiento de la conectividad, permitiendo múltiples componentes conectados en el grafo, llamaremos a esta última estructura un bosque'.
Tipos de árboles binarios[editar]
Un árbol binario es un árbol en el que ningún nodo puede tener más de dos subárboles. En un árbol binario cada nodo puede tener cero, uno o dos hijos (subárboles). Se conoce el nodo de la izquierda como hijo izquierdo y el nodo de la derecha como hijo derecho.
Existen tipos de árboles binarios que suelen usarse para fines específicos, como:
Implementación en C[editar]
Un árbol binario puede declararse de varias maneras. Algunas de ellas son:
Estructura con manejo de memoria dinámica, siendo el puntero que apunta al árbol de tipo tArbol:
typedef struct nodo {
int clave;
struct nodo *izdo, *dcho;
}Nodo;
Estructura con arreglo indexado:
typedef struct tArbol
{
int clave;
tArbol hIzquierdo, hDerecho;
} tArbol;
tArbol árbol[NUMERO_DE_NODOS];
En el caso de un árbol binario casi-completo (o un árbol completo), puede utilizarse un sencillo arreglo de enteros con tantas posiciones como nodos deba tener el árbol. La información de la ubicación del nodo en el árbol es implícita a cada posición del arreglo. Así, si un nodo está en la posición i, sus hijos se encuentran en las posiciones 2i+1 y 2i+2, mientras que su padre (si tiene), se encuentra en la posición truncamiento((i-1)/2) (suponiendo que la raíz está en la posición cero). Este método se beneficia de un almacenamiento más compacto y una mejor localidad de referencia, particularmente durante un recorrido en preorden. La estructura para este caso sería por tanto:
int árbol[NUMERO_DE_NODOS];
Recorridos sobre árboles binarios[editar]
Recorridos en profundidad[editar]
El método de este recorrido es tratar de encontrar de la cabecera a la raíz en nodo de unidad binaria. Ahora pasamos a ver la implementación de los distintos recorridos:
Recorrido en preorden[editar]
En este tipo de recorrido se realiza cierta acción (quizás simplemente imprimir por pantalla el valor de la clave de ese nodo) sobre el nodo actual y posteriormente se trata el subárbol izquierdo y cuando se haya concluido, el subárbol derecho. Otra forma para entender el recorrido con este método sería seguir el orden: nodo raíz, nodo izquierda, nodo derecha.
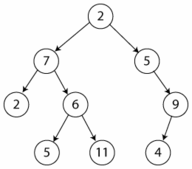
En el árbol de la figura el recorrido en preorden sería: 2, 7, 2, 6, 5, 11, 5, 9 y 4.
void preorden(tArbol *a)
{
if (a != NULL) {
tratar(a); //Realiza una operación en nodo
preorden(a->hIzquierdo);
preorden(a->hDerecho);
}
}
Implementación en pseudocódigo de forma iterativa:
push(s,NULL); //insertamos en una pila (stack) el valor NULL, para asegurarnos de que esté vacía
push(s,raíz); //insertamos el nodo raíz
MIENTRAS (s <> NULL) HACER
p = pop(s); //sacamos un elemento de la pila
tratar(p); //realizamos operaciones sobre el nodo p
SI (D(p) <> NULL) //preguntamos si p tiene árbol derecho
ENTONCES push(s,D(p));
FIN-SI
SI (I(p) <> NULL) //preguntamos si p tiene árbol izquierdo
ENTONCES push(s,I(p));
FIN-SI
FIN-MIENTRAS
Recorrido en postorden[editar]
En este caso se trata primero el subárbol izquierdo, después el derecho y por último el nodo actual. Otra forma para entender el recorrido con este método sería seguir el orden: nodo izquierda, nodo derecha, nodo raíz. En el árbol de la figura el recorrido en postorden sería: 2, 5, 11, 6, 7, 4, 9, 5 y 2.
void postorden(tArbol *a)
{
if (a != NULL) {
postorden(a->hIzquiedo);
postorden(a->hDerecho);
tratar(a); //Realiza una operación en nodo
}
}
Recorrido en inorden[editar]
En este caso se trata primero el subárbol izquierdo, después el nodo actual y por último el subárbol derecho. En un ABB este recorrido daría los valores de clave ordenados de menor a mayor. Otra forma para entender el recorrido con este método sería seguir el orden: nodo izquierda, nodo raíz, nodo derecha. En el árbol de la figura el recorrido en inorden sería: 2, 7, 5, 6, 11, 2, 5, 4, 9.
Esquema de implementación:
void inorden(tArbol *a)
{
if (a != NULL) {
inorden(a->hIzquierdo);
tratar(a); //Realiza una operación en nodo
inorden(a->hDerecho);
}
}
Recorridos en amplitud (o por niveles)[editar]
En este caso el recorrido se realiza en orden por los distintos niveles del árbol. Así, se comenzaría tratando el nivel 1, que solo contiene el nodo raíz, seguidamente el nivel 2, el 3 y así sucesivamente. En el árbol de la figura el recorrido en amplitud sería: 2, 7, 5, 2, 6, 9, 5, 11 y 4.
Al contrario que en los métodos de recorrido en profundidad, el recorrido por niveles no es de naturaleza recursiva. Por ello, se debe utilizar una cola para recordar los subárboles izquierdos y derecho de cada nodo.
El esquema algoritmo para implementar un recorrido por niveles es exactamente el mismo que el utilizado en la versión iterativa del recorrido en preorden pero cambiando la estructura de datos que almacena los nodos por una cola.
Implementación en C:
void arbol_recorrido_anch (tipo_Arbol* A) {
tipo_Cola cola_nodos; // esta cola esta implementada previamente, almacena punteros (posiciones de nodos de árbol)
tipo_Pos nodo_actual; // este es un puntero llevara el recorrido
if (vacio(A)) // si el árbol esta vacio, salimos
return;
cola_inicializa(&cola_nodos); // obvio, y necesario
cola_enqueue(A, &cola_nodos); // se encola la raíz
while (!vacia(&cola_nodos)) { // mientras la cola no se vacie se realizara el recorrido
nodo_actual = cola_dequeue(&cola_nodos) // de la cola saldran los nodos ordenados por nivel
printf("%c,", nodo_actual->info); // se "procesa" el nodo donde va el recorrido, en este caso se imprime
if (nodo_actual->izq != null) // si existe, ponemos el hijo izquierdo en la cola
cola_enqueue(nodo_actual->izq, &cola_nodos);
if (nodo_actual->der != null) // si existe, ponemos el hijo derecho en la cola
cola_enqueue(nodo_actual->der, &cola_nodos);
} // al vaciarse la cola se han visitado todos los nodos del árbol
}
Creación de árboles a partir de los recorridos[editar]
Para poder dibujar un árbol binario sobre la base de los recorridos, se necesitan por lo menos dos de los recorridos de profundidad (en caso de que no se repitan los nodos, ya que si se repiten los nodos es recomendable tener los tres recorridos), ya sean inorden y preorden o inorden y postorden, la única diferencia entre usar el recorrido en preorden o postorden es que en preorden se usa el primer nodo para encontrar la raíz y en postorden se usa el último nodo.
El método consiste en ir dividiendo los recorridos del árbol en pequeños subárboles, se va encontrando la raíz con el preorden o postorden y se divide en dos subárboles basándonos en el recorrido en inorden. En el caso de que los nodos se repitan es conveniente tener los 3 recorridos para identificar más fácilmente cuál de los nodos es la raíz actual.
Para el árbol de la figura corresponden los siguientes recorridos:
Preorden
Inorden
Postorden
Para encontrar la raíz es necesario tener el recorrido preorden o postorden, ya que la raíz es el primer nodo o el último nodo respectivamente. En este caso la raíz es el .
Una vez encontrada la raíz, es necesario saber su posición en el recorrido inorden, del paso anterior se tiene el nodo , pero existen 2 nodos con ese valor, el primero y el de en medio. Si el primer dos es la raíz, entonces no existe ninguna rama del lado izquierdo, en ese caso la siguiente raíz de acuerdo con el recorrido en postorden es y de acuerdo con preorden es , lo cual es una incongruencia, de esa forma sabemos que el otro es la raíz.
Entonces marcamos la raíz en el recorrido inorden:
Preorden
Inorden
Postorden
El recorrido inorden, es un recorrido de los árboles binarios en los que se empieza desde el nodo que se encuentra más a la izquierda de todos, sigue con la raíz y termina con los nodos del lado derecho, entonces, como en el recorrido inorden ya encontramos la raíz, la parte izquierda representa el subárbol izquierdo y la parte derecha representa el subárbol derecho.
En los recorridos tenemos 5 nodos a la izquierda del y a la derecha se encuentran 3 valores, entonces podemos crear los recorridos para el subárbol izquierdo y el subárbol derecho
| Subárbol izquierdo | Subárbol derecho |
|---|---|
| Preorden | Preorden |
| Inorden | Inorden |
| Postorden | Postorden |
Se sigue repitiendo el proceso hasta encontrar todos los nodos del árbol, en este punto la siguiente raíz izquierda es el y la raíz derecha el .
Cuando se llegan a nodos en los que únicamente cuentan con una rama es necesario saber que rama es la derecha y cuál es la izquierda (para algunos árboles con balanceo como los AVL), por ejemplo siguiendo la rama de la derecha partiendo de que el es la raíz el recorrido inorden es entonces el siguiente nodo va a la derecha, no hay nodo a la izquierda, después, los recorridos para el subárbol son:
Preorden
Inorden
Postorden
Finalmente el siguiente nodo se coloca a la izquierda del .
Este método es 100% efectivo cuando no existen nodos repetidos, cuando los nodos se repiten la complejidad aumenta para poder descubrir cuál es el nodo raíz en el recorrido inorden.
Métodos para almacenar Árboles Binarios[editar]
Los árboles binarios pueden ser construidos a partir de lenguajes de programación de varias formas. En un lenguaje con registros y referencias, los árboles binarios son construidos típicamente con una estructura de nodos y punteros en la cual se almacenan datos, cada uno de estos nodos tiene una referencia o puntero a un nodo izquierdo y a un nodo derecho denominados hijos. En ocasiones, también contiene un puntero a un único nodo. Si un nodo tiene menos de dos hijos, algunos de los punteros de los hijos pueden ser definidos como nulos para indicar que no dispone de dicho nodo. En la figura adjunta se puede observar la estructura de dicha implementación.
Los árboles binarios también pueden ser almacenados como una estructura de datos implícita en vectores, y si el árbol es un árbol binario completo, este método no desaprovecha el espacio en memoria. Tomaremos como notación la siguiente: si un nodo tiene un índice i, sus hijos se encuentran en índices 2i + 1 y 2i + 2, mientras que sus padres (si los tiene) se encuentra en el índice (partiendo de que la raíz tenga índice cero). Este método tiene como ventajas el tener almacenados los datos de forma más compacta y por tener una forma más rápida y eficiente de localizar los datos en particular durante un preoden transversal. Sin embargo, desperdicia mucho espacio en memoria.
Codificación de árboles n-arios como árboles binarios[editar]
Hay un mapeo uno a uno entre los árboles generales y árboles binarios, el cual en particular es usado en Lisp para representar árboles generales como árboles binarios. Cada nodo N ordenado en el árbol corresponde a un nodo N' en el árbol binario; el hijo de la izquierda de N’ es el nodo correspondiente al primer hijo de N, y el hijo derecho de N' es el nodo correspondiente al siguiente hermano de N, es decir, el próximo nodo en orden entre los hijos de los padres de N.
Esta representación como árbol binario de un árbol general, se conoce a veces como un árbol binario primer hijo hermano, o un árbol doblemente encadenado.
Una manera de pensar acerca de esto es que los hijos de cada nodo estén en una lista enlazada, encadenados junto con el campo derecho, y el nodo solo tiene un puntero al comienzo o la cabeza de esta lista, a través de su campo izquierdo.
Por ejemplo, en el árbol de la izquierda, la A tiene 6 hijos (B, C, D, E, F, G). Puede ser convertido en el árbol binario de la derecha:
El árbol binario puede ser pensado como el árbol original inclinado hacia los lados, con los bordes negros izquierdos representando el primer hijo y los azules representado los siguientes hermanos.
Las hojas del árbol de la izquierda serían escritas en Lisp como:
(((N O) I J) C D ((P) (Q)) F (M))
Que se ejecutará en la memoria como el árbol binario de la derecha, sin ningún tipo de letras en aquellos nodos que tienen un hijo izquierdo.




















