Diferencia entre revisiones de «Teselado uniforme»

Contenido eliminado Contenido añadido

En renglón

Revisión del 11:40 2 sep 2023

En geometría, un teselado uniforme es un tipo de teselado del plano mediante polígonos regulares, que deben ser necesariamente vértice transitivos.

Pueden existir teselados uniformes tanto en el plano euclídeo como en plano hiperbólico. Los teselados uniformes están relacionados con el poliedros uniformes finitos, que pueden considerarse teselados uniformes de la esfera.

La mayoría de los teselados uniformes se pueden generar a partir de una construcción de Wythoff, comenzando con un grupo de simetría y un punto generador singular dentro de dominio fundamental. Un grupo de simetría plana tiene un dominio fundamental poligonal y puede representarse mediante el nombre del grupo denotado a su vez por el orden de los espejos en vértices secuenciales.

Un triángulo de dominio fundamental es (p'q'r), y un triángulo rectángulo (p q 2), donde p, q, r son números enteros mayores que 1. El triángulo puede ser esférico, un triángulo plano euclídeo o un triángulo plano hiperbólico, dependiendo de los valores de p, q y r.

Existen varias clases de símbolos para denominar a estas figuras, a partir de un símbolo de Schläfli modificado para dominios de triángulos rectángulos: (p q 2) → {p, q}. El diagrama de Coxeter-Dynkin es un gráfico triangular con p, q, r etiquetados en las aristas. Si r = 2, la gráfica es lineal, ya que los nodos del dominio de orden 2 no generan reflexiones. El símbolo de Wythoff toma los 3 números enteros y los separa por una barra vertical (|). Si el punto del generador está fuera del espejo opuesto a un nodo de dominio, se indica antes de la barra.

Finalmente, los teselados se pueden describir por su configuración de vértices, la secuencia de polígonos alrededor de cada vértice.

Todos los teselados uniformes se pueden construir a partir de varias operaciones aplicadas a los teselados regulares. Estas operaciones, según la nomenclatura ideada por Norman Johnson, se denominan truncamiento (cortado de vértices), rectificación (cortado de vértices hasta hacer desaparecer las aristas originales) y canteado (cortado de aristas). El Omnitruncamiento es una operación que combina truncamiento y canteado. El achatado es una operación de truncamiento alternado de la forma omnitruncada (véase poliedro uniforme para obtener más detalles).

Grupos de Coxeter

Los Grupo de Coxeter para el plano definen la construcción de Wythoff y pueden representarse mediante Diagrama de Coxeter-Dynkin:

Para grupos con pedidos de números enteros, que incluyen:

Euclidean plane
Orbifold symmetry	Grupo de Coxeter			notes
Compact
*333	(3 3 3)	${\tilde {A}}_{2}$	[3^[3]]	3 reflective forms, 1 snub
*442	(4 4 2)	${\tilde {B}}_{2}$	[4,4]	5 reflective forms, 1 snub
*632	(6 3 2)	${\tilde {G}}_{2}$	[6,3]	7 reflective forms, 1 snub
*2222	(∞ 2 ∞ 2)	${\tilde {I}}_{1}$ × ${\tilde {I}}_{1}$	[∞,2,∞]	3 reflective forms, 1 snub
Noncompact (frieze)
*∞∞	(∞)	${\tilde {I}}_{1}$	[∞]
*22∞	(2 2 ∞)	${\tilde {I}}_{1}$ × ${\tilde {A}}_{2}$	[∞,2]	2 reflective forms, 1 snub

Hyperbolic plane
Orbifold symmetry	Grupo de Coxeter		notes
Compact
*pq2	(p q 2)	[p,q]	2(p+q) < pq
*pqr	(p q r)	[(p,q,r)]	pq+pr+qr < pqr
Paracompact
*∞p2	(p ∞ 2)	[p,∞]	p>=3
*∞pq	(p q ∞)	[(p,q,∞)]	p,q>=3, p+q>6
*∞∞p	(p ∞ ∞)	[(p,∞,∞)]	p>=3
*∞∞∞	(∞ ∞ ∞)	[(∞,∞,∞)]

Teselados uniformes del plano euclidiano

Véase también: Anexo:Teselados k-uniformes

Hay grupos de simetría en el plano euclidiano construidos a partir de triángulos fundamentales: (4 4 2), (6 3 2) y (3 3 3). Cada uno está representado por un conjunto de líneas de reflexión que dividen el plano en triángulos fundamentales.

Estos grupos de simetría crean 3 teselado regular y 7 semirregulares. Varios de los teselados semirregulares se repiten a partir de diferentes constructores de simetría.

Un grupo de simetría prismática representado por (2 2 2 2) está representado por dos conjuntos de espejos paralelos, que en general pueden tener un dominio fundamental rectangular. No genera nuevos teselados.

Otro grupo de simetría prismática representado por (∞ 2 2) que tiene un dominio fundamental infinito. Construye dos teselados uniformes, prisma apeirogonal y antiprisma apeirogonal.

El apilamiento de las caras finitas de estos dos teselados prismáticos construye un teselado uniforme construcción de Wythoff del plano. Se llama elongated triangular tiling y está compuesto por capas alternas de cuadrados y triángulos.

Triángulos fundamentales de ángulo recto: (p q 2)

(p q 2)	Fund. triangles	Parent	Truncated	Rectified	Bitruncated	Birectified (dual)	Cantellated	Omnitruncated (Cantitruncated)	Snub
Wythoff symbol		q \| p 2	2 q \| p	2 \| p q	2 p \| q	p \| q 2	p q \| 2	p q 2 \|	\| p q 2
Símbolo de Schläfli		{p,q}	t{p,q}	r{p,q}	2t{p,q}=t{q,p}	2r{p,q}={q,p}	rr{p,q}	tr{p,q}	sr{p,q}
Diagrama de Coxeter-Dynkin
Vertex config.		p^q	q.2p.2p	(p.q)²	p. 2q.2q	q^p	p. 4.q.4	4.2p.2q	3.3.p. 3.q
Teselado cuadrado (4 4 2)	0	{4,4}	4.8.8	4.4.4.4	4.8.8	{4,4}	4.4.4.4	4.8.8	3.3.4.3.4
Teselado hexagonal (6 3 2)	0	{6,3}	3.12.12	3.6.3.6	6.6.6	{3,6}	3.4.6.4	4.6.12	3.3.3.3.6

Triángulos fundamentales generales: (p q r)

Wythoff symbol (p q r)	Fund. triangles	q \| p r	r q \| p	r \| p q	r p \| q	p \| q r	p q \| r	p q r \|	\| p q r
Diagrama de Coxeter-Dynkin
Vertex config.		(p.q)^r	r.2p.q.2p	(p.r)^q	q.2r.p. 2r	(q.r)^p	q.2r.p. 2r	r.2q.p. 2q	3.r.3.q.3.p
Triangular (3 3 3)	0	(3.3)³	3.6.3.6	(3.3)³	3.6.3.6	(3.3)³	3.6.3.6	6.6.6	3.3.3.3.3.3

Dominios fundamentales no simples

El único dominio fundamental posible en el espacio 2 euclidiano que no es un símplex es el rectángulo (∞ 2 ∞ 2), con Diagrama de Coxeter-Dynkin: . Todos los formularios generados a partir de él se convierten en teselado cuadrado.

teselados uniformes del plano hiperbólico

Véase también: Uniform tilings in hyperbolic plane

Hay infinitos teselados uniformes de polígonos regulares convexos en el hyperbolic plane, cada uno basado en un grupo de simetría reflectante diferente (p q r).

Aquí se muestra una muestra con una proyección Poincaré disk.

El Diagrama de Coxeter-Dynkin se presenta en forma lineal, aunque en realidad es un triángulo, con el segmento final r conectado al primer nodo.

Existen más grupos de simetría en el plano hiperbólico con dominios fundamentales cuadriláteros que comienzan con (2 2 2 3), etc., que pueden generar nuevas formas. Además, existen dominios fundamentales que colocan los vértices en el infinito, como (∞ 2 3), etc.

Triángulos fundamentales de ángulo recto: (p q 2)

(p q 2)	Fund. triangles	Parent	Truncated	Rectified	Bitruncated	Birectified (dual)	Cantellated	Omnitruncated (Cantitruncated)	Snub
Wythoff symbol		q \| p 2	2 q \| p	2 \| p q	2 p \| q	p \| q 2	p q \| 2	p q 2 \|	\| p q 2
Símbolo de Schläfli		t{p,q}	t{p,q}	r{p,q}	2t{p,q}=t{q,p}	2r{p,q}={q,p}	rr{p,q}	tr{p,q}	sr{p,q}
Diagrama de Coxeter-Dynkin
Vertex figure		p^q	(q.2p.2p)	(p.q.p.q)	(p. 2q.2q)	q^p	(p. 4.q.4)	(4.2p.2q)	(3.3.p. 3.q)
(5 4 2)	V4.8.10	{5,4}	4.10.10	4.5.4.5	5.8.8	{4,5}	4.4.5.4	4.8.10	3.3.4.3.5
(5 5 2)	V4.10.10	{5,5}	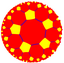5.10.10	5.5.5.5	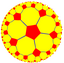5.10.10	{5,5}	5.4.5.4	4.10.10	3.3.5.3.5
(7 3 2)	V4.6.14	{7,3}	3.14.14	3.7.3.7	7.6.6	{3,7}	3.4.7.4	4.6.14	3.3.3.3.7
(8 3 2)	V4.6.16	{8,3}	3.16.16	3.8.3.8	8.6.6	{3,8}	3.4.8.4	4.6.16	3.3.3.3.8

Triángulos fundamentales generales (p q r)

Wythoff symbol (p q r)	Fund. triangles	q \| p r	r q \| p	r \| p q	r p \| q	p \| q r	p q \| r	p q r \|	\| p q r
Diagrama de Coxeter-Dynkin
Vertex figure		(p.r)^q	(r.2p.q.2p)	(p.q)^r	(q.2r.p. 2r)	(q.r)^p	(r.2q.p. 2q)	(2p.2q.2r)	(3.r.3.q.3.p)
(4 3 3)	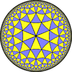V6.6.8	(3.4)³	3.8.3.8	(3.4)³	3.6.4.6	(3.3)⁴	3.6.4.6	6.6.8	3.3.3.3.3.4
(4 4 3)	V6.8.8	(3.4)⁴	3.8.4.8	(4.4)³	3.6.4.6	(3.4)⁴	4.6.4.6	6.8.8	3.3.3.4.3.4
(4 4 4)	V8.8.8	(4.4)⁴	4.8.4.8	(4.4)⁴	4.8.4.8	(4.4)⁴	4.8.4.8	8.8.8	3.4.3.4.3.4

Listas ampliadas de teselados uniformes

Hay varias formas de ampliar la lista de teselados uniformes:

Las figuras de vértice pueden tener caras retrógradas y girar alrededor del vértice más de una vez.

Se pueden incluir # teselados Estrella (figura geométrica).

Apeirógono, {∞}, se pueden utilizar como caras de teselado.

También se puede utilizar # Zigzags (apeirogons alternando entre dos ángulos).

La restricción de que los teselados se encuentren de borde a borde se puede relajar, permitiendo teselados adicionales como Pythagorean tiling.

Los triángulos del grupo de simetría con retrógrados incluyen:

(4/3 4/3 2) (6 3/2 2) (6/5 3 2) (6 6/5 3) (6 6 3/2)

Los triángulos del grupo de simetría con infinito incluyen:

(4 4/3 ∞) (3/2 3 ∞) (6 6/5 ∞) (3 3/2 ∞)

Branko Grünbaum y G. C. Shephard, en el libro de 1987 teselados y patrones, en la sección 12.3 enumera una lista de 25 teselados uniformes, incluidas las 11 formas convexas, y agrega 14 más que llaman "teselados huecos" que incluían los dos primeros. expansiones arriba, caras de polígonos estrellados y figuras de vérice

figuras de tex.^[1]

Harold Scott MacDonald Coxeter, M. S. Longuet-Higgins y J. C. P. Miller, en el artículo de 1954 'Poliedros uniformes', en la 'Tabla 8: Teselaciones uniformes', utilizan las tres primeras expansiones y enumeran un total de 38 teselados uniformes. Si se cuenta también un teselado formado por 2 apeirogons, el total puede considerarse 39 teselados uniformes.

En 1981, Grünbaum, Miller y Shephard en su artículo Uniform Tilings with Hollow Tiles enumeraron 25 teselados usando las dos primeras expansiones y 28 más cuando se agrega la tercera (lo que hace 53 usando la definición de Coxeter et al.). Cuando se agrega el cuarto, enumeran 23 teselados uniformes adicionales y 10 familias (8 dependiendo de parámetros continuos y 2 de parámetros discretos).^[2]

Además de las 11 soluciones convexas, a continuación se muestran los 28 teselados de estrellas uniformes enumerados por Coxeter et al., agrupados por gráficos de bordes compartidos, seguidos de 15 más enumerados por Grünbaum et al. que cumplen con Coxeter et al. definición de al., pero no fueron captados por ellos.

Este conjunto no se ha demostrado completo. Por "2,25" se entiende el teselado 25 en la tabla 2 de Grünbaum et al. de 1981.

Los siguientes tres teselados son excepcionales porque solo hay un número finito de un tipo de cara: dos apeirogons en cada uno. A veces no se incluye el teselado apeirogonal de orden 2, ya que sus dos caras se encuentran en más de un borde.

Friso (matemáticas) symmetry
McNeill^[3]	Vertex Config	Wythoff	Symmetry	Notes
I1	∞.∞		p1m1	(Two half-plane tiles, order-2 apeirogonal tiling)
I2	4.4.∞	∞ 2 \| 2	p1m1	Prisma apeirogonal
I3	3.3.3.∞	\| 2 2 ∞	p11g	Antiprisma apeirogonal

Para mayor claridad, los apeirogons no se colorean de aquí en adelante. Se resalta un conjunto de polígonos alrededor de un vértice. McNeill solo enumera los teselados proporcionados por Coxeter et al. (1954). Los once teselados uniformes convexos se han repetido como referencia.

Grupo del papel pintado symmetry
McNeill^[3]	Grünbaum et al 1981^[2]	Edge diagram	Highlighted	Vertex Config	Wythoff	Symmetry
Convex	1.9			4.4.4.4	4 \| 2 4	p4m
I4	2.14			4.∞.4/3.∞ 4.∞.-4.∞	4/3 4 \| ∞	p4m
Convex	1.24			6.6.6	3 \| 2 6	p6m
Convex	1.25			3.3.3.3.3.3	6 \| 2 3	p6m
I5	2.26			(3.∞.3.∞.3.∞)/2	3/2 \| 3 ∞	p3m1
Convex	1.23			3.6.3.6	2 \| 3 6	p6m
I6	2.25			6.∞.6/5.∞ 6.∞.-6.∞	6/5 6 \| ∞	p6m
I7	2.24			∞.3.∞.3/2 3.∞.-3.∞	3/2 3 \| ∞	p6m
Convex	1.14			3.4.6.4	3 6 \| 2	p6m
1	1.15			3/2.12.6.12 -3.12.6.12	3/2 6 \| 6	p6m
1	1.16			4.12.4/3.12/11 4.12.-4.-12	2 6 (3/2 6/2) \|	p6m
Convex	1.5			4.8.8	2 4 \| 4	p4m
2	2.7			4.8/3.∞.8/3	4 ∞ \| 4/3	p4m
	1.7			8/3.8.8/5.8/7 8.8/3.-8.-8/3	4/3 4 (4/2 ∞/2) \|	p4m
	2.6			8.4/3.8.∞ -4.8.∞.8	4/3 ∞ \| 4	p4m
Convex	1.20			3.12.12	2 3 \| 6	p6m
3	2.17			6.12/5.∞.12/5	6 ∞ \| 6/5	p6m
	1.21			12/5.12.12/7.12/11 12.12/5.-12.-12/5	6/5 6 (6/2 ∞/2) \|	p6m
	2.16			12.6/5.12.∞ -6.12.∞.12	6/5 ∞ \| 6	p6m
4	1.18			12/5.3.12/5.6/5 3.12/5.-6.12/5	3 6 \| 6/5	p6m
	1.19			12/5.4.12/7.4/3 4.12/5.-4.-12/5	2 6/5 (3/2 6/2) \|	p6m
	1.17			4.3/2.4.6/5 3.-4.6.-4	3/2 6 \| 2	p6m
5	2.5			8.8/3.∞	4/3 4 ∞ \|	p4m
6	2.15			12.12/5.∞	6/5 6 ∞ \|	p6m
7	1.6		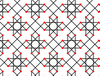	8.4/3.8/5 4.-8.8/3	2 4/3 4 \|	p4m
Convex	1.11			4.6.12	2 3 6 \|	p6m
8	1.13		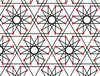	6.4/3.12/7 4.-6.12/5	2 3 6/5 \|	p6m
9	1.12			12.6/5.12/7 6.-12.12/5	3 6/5 6 \|	p6m
10	1.8		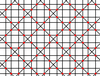	4.8/5.8/5 -4.8/3.8/3	2 4 \| 4/3	p4m
11	1.22		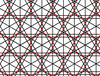	12/5.12/5.3/2 -3.12/5.12/5	2 3 \| 6/5	p6m
Convex	1.1			3.3.3.4.4	construcción de Wythoff	cmm
12	1.2			4.4.3/2.3/2.3/2 3.3.3.-4.-4	No wythoffiano	cmm
Convex	1.3			3.3.4.3.4	\| 2 4 4	p4g
13	1.4			4.3/2.4.3/2.3/2 3.3.-4.3.-4	\| 2 4/3 4/3	p4g
14	2.4			3.4.3.4/3.3.∞ 3.4.3.-4.3.∞	\| 4/3 4 ∞	p4
Convex	1.10			3.3.3.3.6	\| 2 3 6	p6
rowspan=2	2.1	rowspan=2		3/2.∞.3/2.∞.3/2.4/3.4/3 3.4.4.3.∞.3.∞	No wythoffiano	cmm
2.2		3/2.∞.3/2.∞.3/2.4.4 3.-4.-4.3.∞.3.∞	No wythoffiano	cmm
	2.3			3/2.∞.3/2.4.4.3/2.4/3.4/3 3.4.4.3.-4.-4.3.∞	No wythoffiano	p3
rowspan=2	2.8	rowspan=2		4.∞.4/3.8/3.8 4.8.8/3.-4.∞	No wythoffiano	p4m
2.9		4.∞.4.8.8/3 -4.8.8/3.4.∞	No wythoffiano	p4m
rowspan=4	2.10	rowspan=4		4.∞.4/3.8.4/3.8 4.8.-4.8.-4.∞	No wythoffiano	p4m
2.11		4.∞.4/3.8.4/3.8 4.8.-4.8.-4.∞	No wythoffiano	p4g
2.12		4.∞.4/3.8/3.4.8/3 4.8/3.4.8/3.-4.∞	No wythoffiano	p4m
2.13		4.∞.4/3.8/3.4.8/3 4.8/3.4.8/3.-4.∞	No wythoffiano	p4g
rowspan=6	2.18	rowspan=6		3/2.∞.3/2.4/3.4/3.3/2.4/3.4/3 3.4.4.3.4.4.3.∞	No wythoffiano	p6m
2.19		3/2.∞.3/2.4.4.3/2.4.4 3.-4.-4.3.-4.-4.3.∞	No wythoffiano	p6m
2.20		3/2.∞.3/2.∞.3/2.12/11.6.12/11 3.12.-6.12.3.∞.3.∞	No wythoffiano	p6m
2.21		3/2.∞.3/2.∞.3/2.12.6/5.12 3.-12.6.-12.3.∞.3.∞	No wythoffiano	p6m
2.22		3/2.∞.3/2.∞.3/2.12/7.6/5.12/7 3.12/5.6.12/5.3.∞.3.∞	No wythoffiano	p6m
2.23		3/2.∞.3/2.∞.3/2.12/5.6.12/5 3.-12/5.-6.-12/5.3.∞.3.∞	No wythoffiano	p6m

Hay dos teselados uniformes para la figura del vértice 4.8.-4.8.-4.∞ (Grünbaum et al. 2.10 y 2.11) y también dos teselados uniformes para la figura del vértice 4.8/3.4.8/3.-4.∞ (Grünbaum et al. 2.12 y 2.13), con diferentes simetrías. También hay un tercer teselado para cada figura de vértice que es solo pseudo-uniform (los vértices vienen en dos órbitas de simetría). Usan diferentes conjuntos de caras cuadradas. Por lo tanto, para los teselados euclidianos de estrellas, la figura del vértice no determina necesariamente el teselado.^[2]

En las imágenes siguientes, los cuadrados incluidos con bordes horizontales y verticales están marcados con un punto central. Un solo cuadrado tiene los bordes resaltados.^[2]

2.10 and 2.12 (p4m)
2.11 and 2.13 (p4g)
Pseudo-uniform

Los teselados con zigzags se enumeran a continuación. La notación {∞^α} denota un zigzag con ángulo 0 < &alfa; < Π. El apeirogon puede considerarse como el caso especial α = π. Las simetrías se dan para el caso genérico: a veces hay valores especiales de α que aumentan la simetría. Los teselados 3.1 y 3.12 pueden incluso volverse regulares; 3.32 ya lo es (no tiene parámetros libres). A veces hay valores especiales de α que provocan la degeneración del teselado.^[2]

Tilings with zigzags
Grünbaum et al 1981^[2]	Diagram	Vertex Config	Symmetry
3.1		∞^α.∞^β.∞^γ α+β+γ=2π	p2
3.2		∞^α.∞^β.-∞^α+β 0<α+β≤π	p2
3.3		3.3.∞^π-α.-3.∞^α+2π/3 0≤α≤π/6	pgg
3.4		3.3.-∞^π-α.-3.∞^−α+2π/3 0≤α<π/3	pgg
3.5		4.4.∞^φ.4.4.-∞^φ φ=2 arctan(n/k), nk even, (n,k)=1 drawn for φ=2 arctan 2	pmg
3.6		4.4.∞^φ.-4.-4.∞^φ φ=2 arctan(n/k), nk even, (n,k)=1 drawn for φ=2 arctan 1/2	pmg
3.7		3.4.4.3.-∞^2π/3.-3.-∞^2π/3	cmm
3.8		3.-4.-4.3.-∞^2π/3.-3.-∞^2π/3	cmm
3.9		4.4.∞^π/3.∞.-∞^π/3	p2
3.10		4.4.∞^2π/3.∞.-∞^2π/3	p2
3.11		∞.∞^α.∞.∞^−α 0<α<π	cmm
3.12		∞^α.∞^π-α.∞^α.∞^π-α 0<α≤π/2	cmm
3.13		3.∞^α.-3.-∞^α π/3<α<π	p31m
3.14		4.4.∞^2π/3.4.4.-∞^2π/3	p31m
3.15		4.4.∞^π/3.-4.-4.-∞^π/3	p31m
3.16		4.∞^α.-4.-∞^α 0<α<π, α≠π/2	p4g
3.17		4.-8.∞^π/2.∞.-∞^π/2.-8	cmm
3.18		4.-8.∞^π/2.∞.-∞^π/2.-8	p4
3.19		4.8/3.∞^π/2.∞.-∞^π/2.8/3	cmm
3.20		4.8/3.∞^π/2.∞.-∞^π/2.8/3	p4
3.21		6.-12.∞^π/3.∞.-∞^π/3.-12	p6
3.22		6.-12.∞^2π/3.∞.-∞^2π/3.-12	p6
3.23		6.12/5.∞^π/3.∞.-∞^π/3.12/5	p6
3.24		6.12/5.∞^2π/3.∞.-∞^2π/3.12/5	p6
3.25		3.3.3.∞^2π/3.-3.∞^2π/3	p31m
3.26		3.∞.3.-∞^2π/3.-3.-∞^2π/3	cm
3.27		3.∞.-∞^2π/3.∞.-∞^2π/3.∞	p31m
3.28		3.∞^2π/3.∞^2π/3.-3.-∞^2π/3.-∞^2π/3	p31m
3.29		∞.∞^π/3.∞^π/3.∞.-∞^π/3.-∞^π/3	cmm
3.30		∞.∞^π/3.-∞^2π/3.∞.∞^2π/3.-∞^π/3	p2
3.31		∞.∞^2π/3.∞^2π/3.∞.-∞^2π/3.-∞^2π/3	cmm
3.32		∞^π/3.∞^π/3.∞^π/3.∞^π/3.∞^π/3.∞^π/3	p6m
3.33		∞^π/3.-∞^2π/3.-∞^2π/3.∞^π/3.-∞^2π/3.-∞^2π/3	cmm

Los pares de teselados 3.17 y 3.18, así como 3.19 y 3.20, tienen configuraciones de vértices idénticas pero simetrías diferentes.^[2]

Los teselados 3.7 a 3.10 tienen la misma disposición de bordes que 2.1 y 2.2; 3.17 a 3.20 tienen la misma disposición de bordes que 2.10 a 2.13; 3.21 a 3.24 tienen la misma disposición de bordes que 2.18 a 2.23; y del 3,25 al 3,33 tienen la misma disposición de bordes que el 1,25 (el teselado triangular normal).^[2]

Teselados autoduales

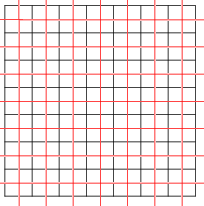
The {4,4} teselado cuadrado (black) with its dual (red).

Los teselados también pueden ser autoduales. El teselado cuadrado, con Símbolo de Schläfli {4,4}, es autodual; Aquí se muestran dos teselados cuadrados (rojo y negro), duales entre sí.

Teselados uniformes usando polígonos en estrella

Ver un star polygon como un polígono no convexo con el doble de lados permite polígonos en estrella, y contarlos como polígonos regulares permite usarlos en un "teselado uniforme". Estos polígonos están etiquetados como {N_α} para un góno 2N no convexo isotoxal con ángulo diédrico externo α. Sus vértices externos están etiquetados como N*
α y sus vértices internos como N**
α. Esta ampliación de la definición requiere que las esquinas con solo 2 polígonos no se consideren vértices. El teselado se define por su configuración de vértices como una secuencia cíclica de polígonos convexos y no convexos alrededor de cada vértice. Hay 4 teselados uniformes con ángulos ajustables α y 18 teselados uniformes que solo funcionan con ángulos específicos; dando un total de 22 teselados uniformes que utilizan polígonos de estrellas.^[4]

Todos estos teselados están relacionados topológicamente con los teselados uniformes ordinarios con polígonos regulares convexos, con vértices de 2 valencias ignorados y caras cuadradas como digones, reducidas a una sola arista.

4 uniform tilings with star polygons, angle α
3.6* α.6** α Topological 3.12.12	4.4* α.4** α Topological 4.8.8	6.3* α.3** α Topological 6.6.6	3.3* α.3.3** α Topological 3.6.3.6

18 uniform tilings with star polygons
4.6.4* π/6.6 Topological 4.4.4.4	(8.4* π/4)² Topological 4.4.4.4	12.12.4* π/3 Topological 4.8.8	3.3.8* π/12.4** π/3.8* π/12 Topological 4.8.8	3.3.8* π/12.3.4.3.8* π/12 Topological 4.8.8	3.4.8.3.8* π/12 Topological 4.8.8
5.5.4* 4π/10.5.4* π/10 Topological 3.3.4.3.4	4.6* π/6.6** π/2.6* π/6 Topological 6.6.6	(4.6* π/6)³ Topological 6.6.6	9.9.6* 4π/9 Topological 6.6.6	(6.6* π/3)² Topological 3.6.3.6	(12.3* π/6)² Topological 3.6.3.6
3.4.6.3.12* π/6 Topological 4.6.12	3.3.3.12* π/6.3.3.12* π/6 Topological 3.12.12	18.18.3* 2π/9 Topological 3.12.12	3.6.6* π/3.6 Topological 3.4.6.4	8.3* π/12.8.6* 5π/12 Topological 3.4.6.4	9.3.9.3* π/9 Topological 3.6.3.6

teselados uniformes usando polígonos alternos

Los polígonos estrella de la forma {p_α} también pueden representar 2p-gónos convexos que alternan dos ángulos, siendo el más simple un rombo {2_α}. Al permitirlos como polígonos regulares, se crean teselados más uniformes, con un ejemplo a continuación.

Examples
3.2.6.2* Topological 3.4.6.4	4.4.4.4 Topological 4.4.4.4	(2* π/6.2** π/3)² Topological 4.4.4.4	2* π/6.2* π/6.2 π/3.2 π/3 Topological 4.4.4.4	4.2* π/6.4.2** π/3 Topological 4.4.4.4

Véase también

Referencias

↑ Tiles and Patterns, Table 12.3.1 p.640
↑ ^a ^b ^c ^d ^e ^f ^g ^h Grünbaum, Branko; Miller, J. C. P.; Shephard, G. C. (1981). «Uniform Tilings with Hollow Tiles». En Davis, Chandler; Grünbaum, Branko; Sherk, F. A., eds. The Geometric Vein: The Coxeter Festschrift. Springer. pp. 17-64. ISBN 978-1-4612-5650-2.
↑ ^a ^b Jim McNeill
↑ Tilings and Patterns Branko Gruenbaum, G.C. Shephard, 1987. 2.5 Tilings using star polygons, pp.82-85.

Bibliografía

Norman Johnson Politopos uniformes, Manuscrito (1991)
- N.W. Johnson: La teoría de los politopos uniformes y los panales, Ph.D. Disertación, Universidad de Toronto, 1966
Grünbaum, Branko; Shephard, G. C. (1987). Tilings and Patterns. W. H. Freeman and Company. ISBN 0-7167-1193-1. (sección 12.3 de teselados de estrellas)
Harold Scott MacDonald Coxeter, M. S. Longuet-Higgins, J. C. P. Miller, Poliedros uniformes, 'Phil. Trans. 1954, 246 A, 401-50 JSTOR 91532