Diferencia entre revisiones de «Triángulo de Reuleaux»
Esta obra contiene una traducción derivada del articulo respectivo de Wikipedia en inglés, concretamente la versión válida al dia de la traducción, publicada por sus editores bajo la Licencia de documentación libre de GNU y la Licencia Creative Commons Atribución-CompartirIgual 3.0 Unported. |
|||
| Línea 17: | Línea 17: | ||
Cada uno de los ángulos de un triángulo equilátero es de <math>{\pi \over 3}</math> radianes. Cada uno de los tres arcos es de longitud <math>{\pi \over 3} a</math>. Por tanto el perímetro del triángulo de Reuleaux es <math>\pi a</math>. |
Cada uno de los ángulos de un triángulo equilátero es de <math>{\pi \over 3}</math> radianes. Cada uno de los tres arcos es de longitud <math>{\pi \over 3} a</math>. Por tanto el perímetro del triángulo de Reuleaux es <math>\pi a</math>. |
||
== |
== Usos == |
||
[[Archivo:Rotation of Reuleaux triangle.gif|thumb|Broca de Harry Watts, basada en el triángulo de Reuleaux.]] |
[[Archivo:Rotation of Reuleaux triangle.gif|thumb|Broca de Harry Watts, basada en el triángulo de Reuleaux.]] |
||
| Línea 28: | Línea 28: | ||
* La existencia de los polígonos de Reuleaux es una buena demostración de que el que una figura tenga anchura constante no implica que sea un círculo. |
* La existencia de los polígonos de Reuleaux es una buena demostración de que el que una figura tenga anchura constante no implica que sea un círculo. |
||
* Muchos lápices son fabricados con este perfil, en lugar de los mucho más tradicionales de sección redonda o hexagonal.<ref>{{Cita web |url=http://www.pencilrevolution.com/2006/04/review-of-staedtler-noris-ergosoft-hb/ |título=Copia archivada |fechaacceso=8 de marzo de 2011 |fechaarchivo=13 de enero de 2020 |urlarchivo=https://web.archive.org/web/20200113052951/http://www.pencilrevolution.com/2006/04/review-of-staedtler-noris-ergosoft-hb/ }}</ref> Por lo general son promocionados como más cómodos y producen un agarre adecuado, además de ser menos probable que rueden fuera de las mesas. |
* Muchos lápices son fabricados con este perfil, en lugar de los mucho más tradicionales de sección redonda o hexagonal.<ref>{{Cita web |url=http://www.pencilrevolution.com/2006/04/review-of-staedtler-noris-ergosoft-hb/ |título=Copia archivada |fechaacceso=8 de marzo de 2011 |fechaarchivo=13 de enero de 2020 |urlarchivo=https://web.archive.org/web/20200113052951/http://www.pencilrevolution.com/2006/04/review-of-staedtler-noris-ergosoft-hb/ }}</ref> Por lo general son promocionados como más cómodos y producen un agarre adecuado, además de ser menos probable que rueden fuera de las mesas. |
||
=== Diseño de mecanismos === |
|||
[[File:Luch2 greifer.gif|thumb|upright|left|Mecanismo de avance de película basado en el triángulo de Reuleaux en el proyector soviético Luch-2 de 8 mm.]] |
|||
Otra clase de aplicaciones del triángulo de Reuleaux consiste en utilizarlo como parte de un [[Enganche (mecánico)|enganche mecánico]] que pueda convertir [[rotación alrededor de un eje fijo]] |
|||
en [[movimiento alternativo]].<ref name="onup">{{citation|title=Antiguos y nuevos problemas no resueltos de geometría plana y teoría de números|volume=11|series=Exposiciones matemáticas Dolciani|first1=Victor|last1=Klee|author1-link=Victor Klee|first2=S. |last2=Wagon|author2-link=Stan Wagon|publisher=Cambridge University Press|year=1991|isbn=978-0-88385-315-3|page=21|url=https://books.google.com/books?id=tRdoIhHh3moC&pg=PA21}}.</ref> Estos mecanismos fueron estudiados por Franz Reuleaux. Con la ayuda de la empresa Gustav Voigt, Reuleaux construyó aproximadamente 800 modelos de mecanismos, varios de los cuales incluían el triángulo de Reuleaux.<ref name="cornell" /> Reuleaux utilizó estos modelos en sus investigaciones científicas pioneras sobre su movimiento.<ref>{{citation|title=Matemáticas y estética: New Approaches to an Ancient Affinity|series=CMS Books in Mathematics|editor1-first=Nathalie|editor1-last=Sinclair|editor1-link=Nathalie Sinclair|editor2-first=David|editor2- last=Pimm|editor3-first=William|editor3-last=Higginson|editor=Springer|year=2007|isbn=978-0-387-38145-9|contribution=Experimentando significados en geometría|first1=David W. |last1=Henderson|first2=Daina|last2=Taimina|author2-link=Daina Taimina|pages=58–83|doi=10.1007/978-0-387-38145-9_4|hdl=1813/2714|hdl-access=free}}. Véase en particular [https://books.google.com/books?id=GJBKLnkYyi0C&pg=PA81 p. 81].</ref> Aunque la mayoría de los modelos de Reuleaux-Voigt se han perdido, se han recopilado 219 de ellos en la [[Universidad de Cornell]], incluidos nueve basados en el triángulo de Reuleaux.<ref name="cornell">{{citation|title=La colección Reuleaux de mecanismos cinemáticos de la Universidad de Cornell|first=Francis C. |last=Moon|date=Julio 1999|publisher=Biblioteca de la Universidad de Cornell|url=https://www.asme.org/wwwasmeorg/media/resourcefiles/aboutasme/who%20we%20are/engineering%20history/landmarks/232-reuleaux-collection-of-kinematic-mechanisms-at-cornell-university.pdf|archive-url=https://web.archive.org/web/20200614022856/https://www. asme.org/wwwasmeorg/media/resourcefiles/aboutasme/who%20we%20are/engineering%20history/landmarks/232-reuleaux-collection-of-kinematic-mechanisms-at-cornell-university.pdf|archive-date=14 de junio de 2020}}. </ref><ref name="moon241" /> Sin embargo, el uso de triángulos de Reuleaux en el diseño de mecanismos es anterior a la obra de Reuleaux; por ejemplo, algunas [[máquinas de vapor]] de fecha tan temprana como 1830 tenían una [[leva]] con forma de triángulo de Reuleaux.<ref>{harvtxt|Moon|2007|page=240}}</ref><ref name="mathtrek">{{citation|first=Ivars|last=Peterson|author-link=Ivars Peterson|title=Rolling with Reuleaux|date=19 de octubre de 1996|work=MathTrek|url=https://www.sciencenews.org/article/rolling-reuleaux|publisher=[[ScienceNews]]}}. Reimpreso en {{citation|title=Mathematical Treks: From Surreal Numbers to Magic Circles|series=MAA spectrum|first=Ivars|last=Peterson|author-link=Ivars Peterson|publisher=[[Mathematical Association of America]]|year=2002|isbn=978-0-88385-537-9|pages=141-144|url=https://books.google.com/books?id=4gWSAraVhtAC&pg=PA141}}.</ref> |
|||
Una aplicación de este principio surge en un [[proyector de películas]]. En esta aplicación, es necesario hacer avanzar la película con un movimiento espasmódico y escalonado, en el que cada fotograma de la película se detiene durante una fracción de segundo delante de la lente del proyector, y luego, mucho más rápidamente, la película pasa al siguiente fotograma. Esto se puede hacer utilizando un mecanismo en el que la rotación de un triángulo de Reuleaux dentro de un cuadrado se utiliza para crear un patrón de movimiento para un actuador que tira de la película rápidamente a cada nuevo fotograma y luego hace una pausa en el movimiento de la película mientras se proyecta el fotograma.<ref>{{harvtxt|Lay|2007}}, [https://books.google.com/books?id=U9eOPjmaH90C&pg=PA83 p. 83].</ref> |
|||
El rotor del [[motor Wankel]] tiene forma de triángulo curvilíneo que suele citarse como ejemplo de triángulo de Reuleaux. <ref name="icons"/><ref name="howround"/><ref name="gardner" /><ref name="mathtrek" /> Sin embargo, sus lados curvos son algo más planos que los de un triángulo de Reuleaux, por lo que no tiene una anchura constante.<ref>{{harvtxt|Gruber|1983|page=80}}; {{citation |
|||
| last = Nash | first = David H. |
|||
| date = marzo de 1977 |
|||
| Índice = 10.1080/0025570x.1977.11976621 |
|||
| number = 2 |
|||
| journal = Mathematics Magazine |
|||
| páginas = 87-89 |
|||
| title = Geometría de motores rotativos |
|||
| volumen = 50}}; {{citation |
|||
| last1 = Badr | first1 = O. |
|||
| last2 = Naik first2 = S. |
|||
| last3 = O'Callaghan first3 = P. W. |
|||
| last4 = Probert first4 = S. D. |
|||
| doi = 10.1016/0306-2619(91)90063-4 |
|||
| número = 1 |
|||
| journal = Applied Energy |
|||
| páginas = 59-76 |
|||
| title = Motores Wankel rotativos como dispositivos de expansión en motores de ciclo Rankine de vapor |
|||
| volumen = 39 |
|||
| año = 1991}}.</ref> |
|||
== Generalizaciones == |
== Generalizaciones == |
||
Revisión del 05:57 19 abr 2023
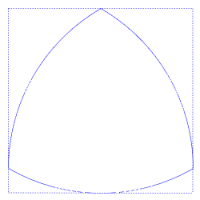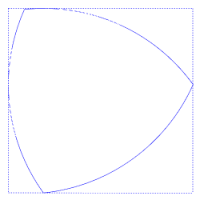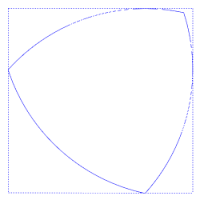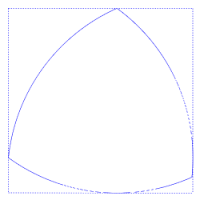
El triángulo Reuleaux es el ejemplo más sencillo de los llamados polígonos de Reuleaux, denominados así por el científico e ingeniero que los desarrolló, Franz Reuleaux. Estos polígonos tienen la particularidad de ser curvas de anchura constante, es decir, que la distancia entre dos rectas tangentes paralelas opuestas es la misma, independientemente de la dirección de esas rectas. Esto puede apreciarse en la figura adjunta, en la que siempre hay cuatro puntos de tangencia con el cuadrado, uno en cada lado.
El área del triángulo de Reuleaux es , donde a es la anchura constante. El área de un círculo de igual diámetro es , que es mayor. Más aún, el teorema de Blaschke-Lebesgue establece que el triángulo de Reuleaux tiene menor superficie que cualquier otra figura de igual anchura constante.
Su perímetro es (véase la explicación en la sección siguiente).
El triángulo de Reuleaux puede generalizarse a otros polígonos regulares con un número impar de lados, como puede ser el caso de las monedas británicas de 20 peniques (basadas en un heptágono).

Trazado del triángulo de Reuleaux
Partiendo de un triángulo equilátero de lado a delíniese, haciendo centro en uno de los vértices del triángulo y con radio a, un arco de circunferencias que una entre sí a los dos vértices restantes, repítase la operación para cada vértice y ya se habrá obtenido el triángulo de Reuleaux buscado. Borrando el triángulo inicial, el espacio central que delimitan en común las tres cirunferencias es el triángulo de Reuleaux, una curva de anchura constante.
Cada uno de los ángulos de un triángulo equilátero es de radianes. Cada uno de los tres arcos es de longitud . Por tanto el perímetro del triángulo de Reuleaux es .
Usos

- Debido a que todos sus diámetros tienen la misma longitud, el triángulo Reuleaux, junto con los demás polígonos regulares de Reuleaux, es la respuesta a la pregunta "Además de un círculo, ¿qué otra forma puede tener una tapa de alcantarilla para que no caiga a través del agujero?"
- El rotor de un Motor Wankel puede fácilmente ser confundido con un triángulo de Reuleaux. Aunque se parece mucho en su aspecto, el rotor Wankel tiene entre vértices una curva algo más plana que la del triángulo de Reuleux y por ello no tiene ancho constante.[1]
- En 1914 el ingeniero británico Harry James Watts patentó (US-Patent 1241175 y siguientes) una broca (llamada de Harry Watts en los países de habla inglesa) con forma de triángulo de Reuleaux. Esta broca va montada en un dispositivo especial que hace que gire un tanto excéntricamente y así puede taladrar un agujero con una forma casi exactamente cuadrada. En la figura se puede ver la rotación de esta broca dentro de un agujero cuadrado. Se ve que solo en las esquinas dicha broca deja cuatro pequeñas áreas sin cubrir, que suman un 1,33% del área del cuadrado.

- Un triángulo de Reuleaux puede rodar fácilmente, pero no funciona bien como rueda debido a que no tiene un centro fijo de rotación. Sin embargo, en la figura adjunta la tabla puede hacerse avanzar de manera perfectamente horizontal. En el rodillo de la izquierda habrá un eje que solo se desplace horizontalmente, mientras que en la sección del rodillo de la derecha, que es un triángulo de Reuleux, todos los puntos tienen algo de movimiento vertical, como se aprecia en la animación de la broca de Harry Watts.
- La existencia de los polígonos de Reuleaux es una buena demostración de que el que una figura tenga anchura constante no implica que sea un círculo.
- Muchos lápices son fabricados con este perfil, en lugar de los mucho más tradicionales de sección redonda o hexagonal.[2] Por lo general son promocionados como más cómodos y producen un agarre adecuado, además de ser menos probable que rueden fuera de las mesas.
Diseño de mecanismos

Otra clase de aplicaciones del triángulo de Reuleaux consiste en utilizarlo como parte de un enganche mecánico que pueda convertir rotación alrededor de un eje fijo en movimiento alternativo.[3] Estos mecanismos fueron estudiados por Franz Reuleaux. Con la ayuda de la empresa Gustav Voigt, Reuleaux construyó aproximadamente 800 modelos de mecanismos, varios de los cuales incluían el triángulo de Reuleaux.[4] Reuleaux utilizó estos modelos en sus investigaciones científicas pioneras sobre su movimiento.[5] Aunque la mayoría de los modelos de Reuleaux-Voigt se han perdido, se han recopilado 219 de ellos en la Universidad de Cornell, incluidos nueve basados en el triángulo de Reuleaux.[4][6] Sin embargo, el uso de triángulos de Reuleaux en el diseño de mecanismos es anterior a la obra de Reuleaux; por ejemplo, algunas máquinas de vapor de fecha tan temprana como 1830 tenían una leva con forma de triángulo de Reuleaux.[7][8]
Una aplicación de este principio surge en un proyector de películas. En esta aplicación, es necesario hacer avanzar la película con un movimiento espasmódico y escalonado, en el que cada fotograma de la película se detiene durante una fracción de segundo delante de la lente del proyector, y luego, mucho más rápidamente, la película pasa al siguiente fotograma. Esto se puede hacer utilizando un mecanismo en el que la rotación de un triángulo de Reuleaux dentro de un cuadrado se utiliza para crear un patrón de movimiento para un actuador que tira de la película rápidamente a cada nuevo fotograma y luego hace una pausa en el movimiento de la película mientras se proyecta el fotograma.[9]
El rotor del motor Wankel tiene forma de triángulo curvilíneo que suele citarse como ejemplo de triángulo de Reuleaux. [10][11][12][8] Sin embargo, sus lados curvos son algo más planos que los de un triángulo de Reuleaux, por lo que no tiene una anchura constante.[13]
Generalizaciones
Las curvas triangulares de anchura constante con ángulos suaves y no agudos pueden obtenerse como el lugar geométrico de los puntos situados a una distancia fija del triángulo de Reuleaux.[14] Otras generalizaciones del triángulo de Reuleaux incluyen superficies en tres dimensiones, curvas de anchura constante con más de tres lados, y los conjuntos de Yanmouti que proporcionan ejemplos extremos de una desigualdad entre anchura, diámetro e inradio.
Versión tridimensional

La intersección de cuatro bolas de radio s centradas en los vértices de un tetraedro regular de lado s se denomina tetraedro de Reuleaux, pero su superficie no es una superficie de anchura constante.[15] Puede, sin embargo, convertirse en una superficie de anchura constante, llamada Tetraedro de Meissner, sustituyendo tres de sus arcos de arista por superficies curvas, las superficies de rotación de un arco circular. Alternativamente, la superficie de revolución de un triángulo de Reuleaux a través de uno de sus ejes de simetría forma una superficie de anchura constante, con volumen mínimo entre todas las superficies de revolución conocidas de anchura constante dada.[16]
Polígonos de Reuleaux
El triángulo de Reuleaux puede generalizarse a polígonos regulares o irregulares con un número impar de lados, dando lugar a un polígono de Reuleaux, una curva de anchura constante formada por arcos circulares de radio constante. La anchura constante de estas formas permite su uso como monedas que pueden utilizarse en máquinas que funcionan con monedas.[12] Aunque las monedas de este tipo en circulación general suelen tener más de tres lados, se ha utilizado un triángulo de Reuleaux para una moneda conmemorativa de Bermudas. [17]
Se pueden utilizar métodos similares para encerrar un polígono simple arbitrario dentro de una curva de anchura constante, cuya anchura es igual al diámetro del polígono dado. La forma resultante consiste en arcos circulares (a lo sumo tantos como lados tenga el polígono), puede construirse algorítmicamente en tiempo lineal, y puede dibujarse con compás y regla.[18] Aunque todos los polígonos de Reuleaux tienen un número impar de lados de arco circular, es posible construir formas de anchura constante con un número par de lados de arco circular de radios variables.[19]
Conjuntos de Yanmouti
Los conjuntos de Yanmouti se definen como los cascos convexos de un triángulo equilátero junto con tres arcos circulares, centrados en los vértices del triángulo y que abarcan el mismo ángulo que el triángulo, con radios iguales que son como máximo iguales a la longitud lateral del triángulo. Así, cuando el radio es suficientemente pequeño, estos conjuntos degeneran en el propio triángulo equilátero, pero cuando el radio es lo más grande posible son iguales al triángulo de Reuleaux correspondiente. Toda forma con anchura w, diámetro d, e inradio r (el radio del círculo más grande posible contenido en la forma) obedece a la desigualdad
y esta desigualdad se convierte en una igualdad para los conjuntos de Yanmouti, lo que demuestra que no es mejorable.[20]
Referencias
- ↑ Ein Wankel-Rotor ist kein Reuleux-Dreieck! (alemán) ¡El rotor Wankel no es un triángulo de Reuleux!.
- ↑ «Copia archivada». Archivado desde el original el 13 de enero de 2020. Consultado el 8 de marzo de 2011.
- ↑ Klee, Victor; Wagon, S. (1991), Antiguos y nuevos problemas no resueltos de geometría plana y teoría de números, Exposiciones matemáticas Dolciani 11, Cambridge University Press, p. 21, ISBN 978-0-88385-315-3..
- ↑ a b Moon, Francis C. (Julio 1999), asme.org/wwwasmeorg/media/resourcefiles/aboutasme/who%20we%20are/engineering%20history/landmarks/232-reuleaux-collection-of-kinematic-mechanisms-at-cornell-university.pdf La colección Reuleaux de mecanismos cinemáticos de la Universidad de Cornell, Biblioteca de la Universidad de Cornell, archivado desde el original el 14 de junio de 2020..
- ↑ Henderson, David W.; Taimina, Daina (2007), «Experimentando significados en geometría», en Springer, Nathalie, ed., Matemáticas y estética: New Approaches to an Ancient Affinity, CMS Books in Mathematics, pp. 58-83, ISBN 978-0-387-38145-9, doi:10.1007/978-0-387-38145-9_4, hdl:1813/2714 Parámetro desconocido
|editor2- last=ignorado (ayuda);|editor1-last=y|editor=redundantes (ayuda).. Véase en particular p. 81. - ↑ Error en la cita: Etiqueta
<ref>no válida; no se ha definido el contenido de las referencias llamadasmoon241 - ↑ {harvtxt|Moon|2007|page=240}}
- ↑ a b Peterson, Ivars (19 de octubre de 1996), «Rolling with Reuleaux», MathTrek (ScienceNews).. Reimpreso en Peterson, Ivars (2002), Mathematical Treks: From Surreal Numbers to Magic Circles, MAA spectrum, Mathematical Association of America, pp. 141-144, ISBN 978-0-88385-537-9..
- ↑ Lay (2007), p. 83.
- ↑ Error en la cita: Etiqueta
<ref>no válida; no se ha definido el contenido de las referencias llamadasicons - ↑ Error en la cita: Etiqueta
<ref>no válida; no se ha definido el contenido de las referencias llamadashowround - ↑ a b Error en la cita: Etiqueta
<ref>no válida; no se ha definido el contenido de las referencias llamadasgardner - ↑ Gruber (1983); Nash, David H. (marzo de 1977), «Geometría de motores rotativos», Mathematics Magazine 50 (2): 87-89 Parámetro desconocido
|Índice=ignorado (ayuda).; Badr, O.; Naik first2 = S.; O'Callaghan first3 = P. W.; Probert first4 = S. D. (1991), «Motores Wankel rotativos como dispositivos de expansión en motores de ciclo Rankine de vapor», Applied Energy 39 (1): 59-76, doi:10.1016/0306-2619(91)90063-4.. - ↑ Banchoff, Thomas; Giblin primer2 = Peter (1994), «Sobre la geometría de curvas circulares a trozos», American Mathematical Monthly 101 (5): 403-416, JSTOR 2974900, MR 1272938, doi:10.2307/2974900..
- ↑ {Weber, Christof (2009), ¿Qué tiene que ver este sólido con una pelota?. Weber también tiene películas de ambos tipos de cuerpos de Meissner girando, así como imágenes interactivas.
- ↑ Campi, Stefano; Colesanti, Andrea; Gronchi, Paolo (1996), Ecuaciones diferenciales parciales y aplicaciones: Collected Papers in Honor of Carlo Pucci - Problemas de mínimos para volúmenes de cuerpos convexos, Lecture Notes in Pure and Applied Mathematics, no. 177, Marcel Dekker, pp. 43-55..
- ↑ Conti, Giuseppe; Paoletti, Raffaella (Octubre 2019), «Triángulo de Reuleaux en arquitectura y aplicaciones», en Magnaghi-Delfino, ed., Faces of Geometry: From Agnesi to Mirzakhani, Lecture Notes in Networks and Systems, Springer, pp. 79-89, S2CID 209976466, doi:10.1007/978-3-030-29796-1_7.
- ↑ Chandru, V.; Venkataraman, R. (1991), Actas del Segundo Simposio Anual ACM-SIAM sobre Algoritmos Discretos (SODA '91)- Cascos circulares y orbiformes de polígonos simples, Society for Industrial and Applied Mathematics, pp. 433-440, ISBN 978-0-89791-376-8..
- ↑ Peterson, Bruce B. (1973), «Propiedades de intersección de curvas de anchura constante», Illinois Journal of Mathematics 17 (3): 411-420, MR 0320885, doi:10.1215/ijm/1256051608..
- ↑ Hernández Cifre, M. A. (2000), «¿Existe un conjunto plano convexo con anchura, diámetro e inradio dados?», American Mathematical Monthly 107 (10): 893-900, JSTOR 2695582, MR 1806918, doi:10.2307/2695582..
Véase también
Enlaces externos
- Shapes of constant width (cut-the-knot)
- Mould, Steve. Numberphile. Brady Haran. Archivado desde el original el 19 de marzo de 2016. Consultado el 29 de noviembre de 2015.
- Weisstein, Eric W. «Reuleaux Triangle». En Weisstein, Eric W, ed. MathWorld (en inglés). Wolfram Research.






