Péndulo

Péndulo simple en movimiento armónico con oscilaciones pequeñas.

Péndulo en la Catedral Metropolitana, Ciudad de México.

El péndulo (del lat. pendŭlus, pendiente)​ es un sistema físico que puede oscilar bajo la acción gravitatoria u otra característica física (elasticidad, por ejemplo) y que está configurado por una masa suspendida de un punto o de un eje horizontal fijos mediante un hilo, una varilla, u otro dispositivo que pueda mantener fijo el sistema.

Existen muy variados tipos de péndulos que, atendiendo a su configuración y usos, reciben los nombres apropiados: péndulo simple, péndulo compuesto, péndulo cicloidal, péndulo doble, péndulo de Foucault, péndulo balístico, péndulo de torsión, péndulo esférico, entre otros.

Sus usos son muy variados: medida del tiempo (reloj de péndulo, metrónomo, ...), medida de la intensidad de la gravedad, etc.

Historia

Réplica del sismómetro de Zhang Heng. El péndulo está contenido en su interior

.

Uno de los primeros usos conocidos de un péndulo fue un dispositivo de sismómetro del siglo I de la dinastía Han científico chino Zhang Heng.​ Su función era balancearse y activar una de una serie de palancas tras ser perturbada por el temblor de un terremoto lejano. ​ Liberada por una palanca, una pequeña bola caía del dispositivo en forma de urna en una de las ocho bocas de sapo de metal que había debajo, en los ocho puntos de la brújula, significando la dirección en la que se encontraba el terremoto.​

Muchas fuentes​​​​ afirman que el astrónomo egipcio del siglo X Ibn Yunus utilizaba un péndulo para medir el tiempo, pero se trata de un error originado en 1684 por el historiador británico Edward Bernard.​​​​

Durante el Renacimiento, se utilizaban grandes péndulos bombeados a mano como fuentes de energía para máquinas manuales de movimiento alternativo, como sierras, fuelles y bombas.​ Leonardo da Vinci hizo muchos dibujos del movimiento de los péndulos, aunque sin darse cuenta de su valor para la medición del tiempo.

1602: Investigaciones de Galileo

El científico italiano Galileo Galilei fue el primero en estudiar las propiedades de los péndulos, comenzando alrededor de 1602.​ El primer informe que se conserva de sus investigaciones está contenido en una carta a Guido Ubaldo dal Monte, desde Padua, fechada el 29 de noviembre de 1602.<ref name="Galileo">{{cite book

| last = Galilei | first = Galileo
| title= Le Opere di Galileo Galilei, Edizione Nazionale
| author-link= Galileo Galilei
| editor-last= Favaro
| editor-first= Antonio
| editor-li

Péndulo simple o matemático

Componentes del peso de la masa pendular.

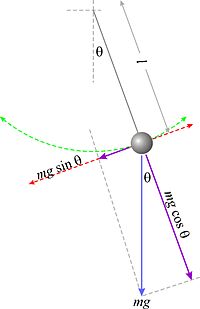
También llamado péndulo ideal, está constituido por un hilo inextensible de masa despreciable, sostenido por su extremo superior de un punto fijo, con una masa puntual sujeta en su extremo inferior que oscila libremente en un plano vertical fijo.

Al separar la masa pendular de su punto de equilibrio, oscila a ambos lados de dicha posición, desplazándose sobre una trayectoria circular con movimiento periódico.

Ecuación del movimiento

Para escribir la ecuación del movimiento observaremos la figura adjunta, correspondiente a una posición genérica del péndulo. La flecha azul representa el peso de la masa pendular. Las flechas en color violeta representan las componentes del peso en las direcciones tangencial y normal a la trayectoria.

Aplicando la Segunda ley de Newton en la dirección del movimiento, tenemos

$F_{\text{t}}=-mg\sin \theta =ma_{\text{t}}\,$

donde el signo negativo tiene en cuenta que la $F_{\text{t}}$ tiene dirección opuesta a la del desplazamiento angular positivo (hacia la derecha, en la figura). Considerando la relación existente entre la aceleración tangencial y la aceleración angular

$a_{\text{t}}=\ell {\ddot {\theta }}\ \,$

obtenemos finalmente la ecuación diferencial del movimiento plano del péndulo simple

$\ell {\ddot {\theta }}\ +g\sin \theta =0\,$

Período de oscilación

Factor de amplificación del período de un péndulo, para una amplitud angular cualquiera. Para ángulos pequeños el factor vale aproximadamente 1 pero tiende a infinito para ángulos cercanos a π (180º).

El astrónomo y físico italiano Galileo Galilei observó que el periodo de oscilación es independiente de la amplitud, al menos para pequeñas oscilaciones. En cambio, aquel depende de la longitud del hilo. El período de la oscilación de un péndulo simple restringido a oscilaciones de pequeña amplitud puede aproximarse por:

$T\approx 2\pi {\sqrt {\ell \over g}}$

Para oscilaciones mayores la relación exacta para el período no es constante con la amplitud e involucra integrales elípticas de primera especie:

$T=4{\sqrt {\ell \over g}}K\left(\sin {\frac {\varphi _{0}}{2}}\right)=4{\sqrt {\ell \over g}}\int _{0}^{\frac {\pi }{2}}{\frac {d\theta }{\sqrt {1-\sin ^{2}{\frac {\varphi _{0}}{2}}\sin ^{2}\theta }}}$

Donde φ₀ es la amplitud angular máxima. La ecuación anterior puede desarrollarse en serie de Taylor obteniéndose una expresión más útil:

$T=2\pi {\sqrt {\ell \over g}}\left[1+\left({\frac {1}{2}}\right)^{2}\sin ^{2}{\frac {\varphi _{0}}{2}}+\left({\frac {1\cdot 3}{2\cdot 4}}\right)^{2}\sin ^{4}{\frac {\varphi _{0}}{2}}+\left({\frac {1\cdot 3\cdot 5}{2\cdot 4\cdot 6}}\right)^{2}\sin ^{6}{\frac {\varphi _{0}}{2}}+\dots \right]$

Solución de la ecuación de movimiento

Para pequeñas oscilaciones la amplitud es casi senoidal, para amplitudes más grandes la oscilación ya no es senoidal. La figura muestra un movimiento de gran amplitud $\phi _{0}=0,999\pi$ (negro), junto a un movimiento de pequeña amplitud $\phi _{0}=0,25\pi$ (gris).

Para amplitudes pequeñas, la oscilación puede aproximarse como combinación lineal de funciones trigonométricas. Para amplitudes grandes puede probarse el ángulo puede expresarse como combinación lineal de funciones elípticas de Jacobi. Para ver esto basta tener en cuenta que la energía constituye una integral de movimiento y usar el método de la cuadratura para integrar la ecuación de movimiento:

$t={\sqrt {\frac {m}{2}}}\int _{0}^{\phi (t)}{\frac {ld\theta }{\sqrt {E-U(\theta )}}}=$ $={\sqrt {\frac {l}{2g}}}\int _{0}^{\phi (t)}{\frac {d\theta }{\sqrt {\cos \theta -\cos \phi _{0}}}}={\sqrt {\frac {l}{4g}}}\int _{0}^{\phi (t)}{\frac {d\theta }{\sqrt {\sin ^{2}{\frac {\phi _{0}}{2}}-\sin ^{2}{\frac {\theta }{2}}}}}$

Donde, en la última expresión se ha usado la fórmula del ángulo doble y donde además:

$E=-mgl\cos \phi _{0}\;$, es la energía, que está relacionada con la máxima amplitud $\phi _{0}\;$.

$U(\phi )=-mgl\cos \phi \;$, es la energía potencial.

Realizando en variable $\sin \xi ={\frac {\sin {\frac {\theta }{2}}}{\sin {\frac {\phi _{0}}{2}}}}\;$, la solución de las ecuaciones del movimiento puede expresarse como:

$t={\sqrt {\frac {l}{g}}}\int _{0}^{\Phi }{\frac {d\xi }{\sqrt {1-\sin ^{2}{\frac {\phi _{0}}{2}}\sin ^{2}\xi }}}\Rightarrow \theta (t)=2\arcsin \left({\mbox{sn}}\ {\sqrt {\frac {g}{l}}}t\cdot \sin {\frac {\phi _{0}}{2}}\right)$

Donde:

${\mbox{sn}}(t)\;$, es la función elíptica de Jacobi tipo seno.

$\sin \Phi ={\frac {\sin {\frac {\phi (t)}{2}}}{\sin {\frac {\phi _{0}}{2}}}}$

El lagrangiano del sistema es ${\mathcal {L}}=T-V={\frac {1}{2}}ml^{2}{\dot {\theta }}^{2}+mgl\cos {\theta }$, donde $\theta$ es el ángulo que forma la cuerda del péndulo a lo largo de sus oscilaciones (es la variable), y $l$ es la longitud de la cuerda (es la ligadura). Si se aplican las ecuaciones de Lagrange se llega a la ecuación final del movimiento: $l^{2}{\ddot {\theta }}+gl\sin {\theta }=0$. Es decir, la masa no influye en el movimiento de un péndulo.

Péndulo esférico

Péndulo de Foucault en el hemisferio sur.

Un péndulo esférico es un sistema con dos grados de libertad. El movimiento está confinado a la una porción de superficie esférica (de radio l) comprendida entre dos paralelos. Existen dos integrales de movimiento, la energía E y la componente del momento angular paralela al eje vertical M_z. La función lagrangiana viene dada por:

$L={\frac {1}{2}}ml^{2}({\dot {\theta }}^{2}+{\dot {\phi }}^{2}\sin ^{2}\theta )+mgl\cos \theta$

Donde $\phi$ es el ángulo polar y $\theta$ es el ángulo que forma el hilo o barra del péndulo con la vertical. Las ecuaciones de movimiento, obtenidas introduciendo el lagrangiano anterior en las ecuaciones de Euler-Lagrange son:

${\begin{matrix}{\cfrac {d}{dt}}{\cfrac {\partial L}{\partial {\dot {\theta }}}}-{\cfrac {\partial L}{\partial \theta }}=0&\Rightarrow &l{\ddot {\theta }}-l{\dot {\phi }}^{2}\sin \theta \cos \theta +g\sin \theta =0\\\\{\cfrac {d}{dt}}{\cfrac {\partial L}{\partial {\dot {\phi }}}}-{\cfrac {\partial L}{\partial \phi }}=0&\Rightarrow &{\cfrac {d}{dt}}(ml^{2}{\dot {\phi }}\sin ^{2}\theta )=0\end{matrix}}$

La segunda ecuación expresa la constancia de la componente Z del momento angular y por tanto lleva a la relación entre la velocidad de giro polar y el momento angular y por tanto a reescribir la lagrangiana como:

${\dot {\phi }}={\frac {M_{z}}{ml^{2}\sin ^{2}\theta }}\Rightarrow \qquad L=K({\dot {\theta }})+U_{ef}(\theta )={\frac {1}{2}}ml^{2}{\dot {\theta }}^{2}+{\frac {M_{z}^{2}}{2ml^{2}\sin ^{2}\theta }}-mgl\cos \theta$

Y el problema queda reducido a un problema unidimensional.

Período

El movimiento de un péndulo esférico en general no resulta periódico, ya que es la combinación de dos movimientos periódicos de períodos generalmente inconmensurables. Sin embargo el movimiento resulta cuasiperiódico, lo cual significa que fijado una posición y una velocidad previas del movimiento existe un tiempo T tal que el movimiento pasará a una distancia tan pequeña como se desee de esa posición con una velocidad tan parecida como se quiera, pero sin repetirse exactamente. Dada que la región de movimiento además resulta compacta, el conjunto de puntos la trayectoria de un péndulo esférico constituye un conjunto denso sobre una área esférica comprendida entre dos casquetes esféricos.

Solución de la ecuación de movimiento

Las ecuaciones de movimiento pueden expresarse en términos de integrales elípticas de primera especie y tercera especie:

$t={\sqrt {\frac {ml^{2}}{2}}}\int {\frac {d\theta }{\sqrt {E-U_{ef}(\theta )}}}\qquad \phi ={\frac {M_{z}}{l{\sqrt {2m}}}}\int {\frac {d\theta }{\sin ^{2}\theta {\sqrt {E-U_{ef}(\theta )}}}}$

Véase también

• péndulo doble
• oscilador armónico
• péndulo balístico
• péndulo cicloidal
• péndulo cónico
• péndulo de Foucault
• péndulo de Newton
• péndulo de Pohl
• péndulo de torsión
• péndulo esférico
• péndulo físico
• péndulo simple
• péndulo simple equivalente
• reloj de péndulo
• teorema de Huygens

Bibliografía

• Matias, Cardozo. (2008). Dinámica clásica de las partículas en fornite. Buenos Aires: Bella Vista. ISBN 84-291-4094-8. 
• Ortega, Manuel R. (1989-2006). Lecciones de Física (4 volúmenes). Monytex. ISBN 84-404-4290-4, ISBN 84-398-9218-7, ISBN 84-398-9219-5, ISBN 84-604-4445-7. 
• Resnick, Robert & Halliday, David (2004). Física 4ª. CECSA, México. ISBN 970-24-0257-3. 

Enlaces externos

• Wikcionario tiene definiciones y otra información sobre péndulo y pendular.
• Péndulo Invertido (enlace roto disponible en Internet Archive; véase el historial, la primera versión y la última).

• Datos: Q20702
• Multimedia: Pendulums / Q20702