Usuario:MRS~eswiki/coeficiente binomial y triángulo de Pascal

versión personal - el artículo oficial de la enciclopedia se encuentra aquí

ALEXANDRA FERIA 11 DE ABRIL 2007 11-08PM--200.115.108.10 18:09 11 abr 2007 (CEST)--200.115.108.10 18:09 11 abr 2007 (CEST)==I Triángulo de Pascal==

El triángulo de Pascal es un triángulo de números enteros, infinito y simétrico cuyas diez primeras líneas han sido representadas en la figura:

Se construye de la siguiente manera: Se empieza por el « 1 » de la cumbre. De una línea a la siguiente se conviene escribir los números con un desfase de media casilla. Así, las casillas (que no se dibujan) tendrán cada una dos casillas justo encima, en la línea anterior. El valor que se escribe en una casilla es la suma de los valores de las dos casillas encima de ella. El valor cero no se escribe.

Por ejemplo, en la última línea dibujada, el cuarto valor es 84 = 28 + 56, suma del tercer y cuarto valor de la línea anterior.

Se observa, y no es difícil demostrarlo, que la capa exterior está formada de unos, la segunda capa de los naturales en orden creciente, que los números no hacen más que subir de una línea a la siguiente y que existe un eje de simetría vertical que pasa por el vértice.

Sin embargo, el interés de este triángulo no radica en estas propiedades, sino en el vínculo que tiene con la álgebra elemental. En efecto, las cifras 1; 2; 1 y 1; 3; 3; 1 recuerdan las identidades:

$(a+b)^{2}=a^{2}+2ab+b^{2}\quad$

y

$(a+b)^{3}=a^{3}+3a^{2}b+3ab^{2}+b^{3}\quad$

pues son los coeficientes de sus monomios. Este parecido no es casual y se generaliza a cualquier potencia del binomio a + b.

II Vínculo entre el triángulo de Pascal y el binomio de Newton

La fórmula que da el desarrollo de $(a+b)^{n}$ según las potencias crecientes de a (y decrecientes de b) se llama binomio de Newton. En esta expresión, lo único que se desconoce son los coeficientes de los monomios $a^{k}b^{n-k}$.

Teorema

Los coeficientes de la forma desarrollada de (a + b)ⁿ son dados
por la línea número n+1 del triángulo de Pascal (la que empieza por 1 y n).

Prueba

Hemos visto mas arriba que era cierto para n = 2 y n = 3. También lo es para n = 0: (a + b)^o = 1 = 1·a^ob⁰ y con n = 1: (a + b)¹ = a + b = 1·a + 1·b.
Para establecer el resultado para cualquier valor de n∈N, lo más natural es proceder por inducción. Suponiendo que es cierto para un valor de n, hay que deducir que lo es también para n+1. En vez de hacerlo en el caso general (sería poco claro) miremos que sucede al pasar de la línea n = 3 a la línea n = 4.

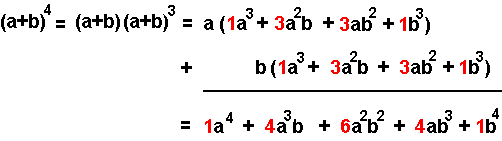
Como lo muestra la figura, el desarrollo de (a + b)⁴ consiste en dos copias del desarrollo de (a + b)³. Están desfasadas (una corresponde a a·(a + b)³ y la otra a b·(a + b)³) y cuando se suman, un mismo coeficiente aparece en una posición dada y otra vez a un paso a la derecha.
Si se considera sólo los coeficientes, inscritos en sendas casillas, obtenemos la suma siguiente:

y obviamente no hace falta escribir dos veces las mismas cifras: la suma consiste en añadir a un coeficiente el coeficiente inmediatamente a su derecha (el 1 con el 3, el 3 con el segundo 3, etc) y esto es justamente lo que se hace en el triángulo de Pascal. En otras palabras, el triángulo simula la multiplicación por a + b, de una línea a la siguiente.

III coeficientes del binomio de Newton

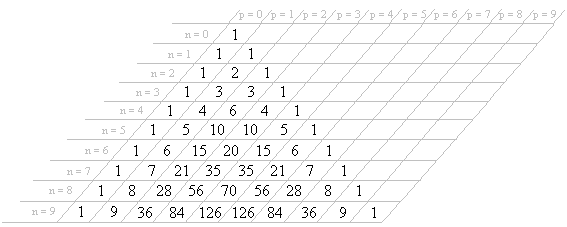
Se inscribe el triángulo de Pascal en una tabla para poder nombrar a cada coeficiente del mismo. El número en la línea n y la columna p se denota:

$n \choose k$

o más raramente

$C_{n}^{k}$

("C" por "combinación") cuando la primera notación no es realizable (por ejemplo en calculadoras de bolsillo, como la TI 82 y familia), y se dice "k entre n", mucho más corto que "coeficiente binomial n,k". Las casillas vacías corresponden a valores nulos.

Por definición misma, tenemos, (para todo n natural):

$(a+b)^{n}=\sum _{k=0}^{n}{n \choose k}a^{k}b^{n-k}$

para cualquier valor de a y b.

De hecho, es una igualdad de polinomios en Z[a,b]. Sin perder en generalidad, resulta a veces más práctica

la "definición" :

$(X+1)^{n}=\sum _{k=0}^{n}{n \choose k}X^{k}$

, vista como una igualdad de polinomios en Z[X].

De esta fórmula se deducen dos consecuencias:

· Tomando X = 1 se obtiene:

$\sum _{k=0}^{n}{n \choose k}=2^{n}$

: la suma de los coeficientes de una misma línea vale 2n.

En efecto: 1 = 2⁰, 1 + 1 = 2 = 2¹, 1 + 2 + 1 = 4 = 2², 1 + 3 + 3 + 1 = 8 = 2³, 1 + 4 + 6 + 4 + 1 = 16 = 2⁴ ...

· Con X = -1 se obtiene, (n > 0):

$\sum _{k=0}^{n}{n \choose k}(-1)^{k}=0$

: la suma alterna de los números de una misma línea vale 0.

En efecto: 1 - 1 = 0, 1 - 2 + 1 = 0, 1 - 3 + 3 - 1 = 0, 1 - 4 + 6 - 4 + 1 = 0, 1 - 5 + 10 - 10 + 5 - 1 = 0 ...

Las propiedades que hemos observado en el triángulo se pueden ahorra escribir con todo rigor:

.

${n \choose 0}={n \choose n}=1$

(costados izquierdos y derechos del triángulo).

.

${n \choose 1}={n \choose {n-1}}=n$

("segunda capa").

.

${n \choose {n-p}}={n \choose p}$

(simetría respecto al eje vertical del triángulo).

.

${n \choose p}=0$

cuando p > n (corresponde a la zona fuera del triángulo).

Y claro, la regla de construcción del triángulo da la relación fundamental de los coeficientes binomiales:

.

${n \choose p}+{n \choose {p+1}}={{n+1} \choose {p+1}}$

IV interpretación en combinatoria

Los coeficientes binomiales son la base misma de la combinatoria. Veamos porque. Tomemos de nuevo un binomio, por ejemplo $(a+b)^{3}$, y desarollémoslo, pero de una manera distinta del párrafo anterior:

$(a+b)^{3}=(a+b)\cdot (a+b)\cdot (a+b)$

luego quitemos las paréntesis, pero sin cambiar el orden en los productos, es decir sin aplicar la conmutatividad:

$(a+b)\cdot (a+b)\cdot (a+b)=(aa+ab+ba+bb)\cdot (a+b)$

$=aaa+aab+aba+abb+baa+bab+bba+bbb\quad$

Y agrupemos los términos que contienen el mismo número de a, (y de b):

$=aaa+(aab+aba+baa)+(abb+bab+bba)+bbb\quad$

El primer paréntesis contiene todas las palabras constituidas de un b y dos a. En este caso, es fácil ver que hay exactamente tres. En el caso general, para contar las palabras, hay que aplicar la conmutatividad, pues las palabras que contienen el mismo número de a y b darán el mismo término:

$=1\cdot a^{3}+3\cdot a^{2}b+3\cdot ab^{2}+1\cdot b^{3}$

El primer factor 3, que es

${3 \choose 1}$

cuenta las tres palabras mensionadas (aab, aba y baa).

El segundo factor 3, que es

${3 \choose 2}$

cuenta las palabras hechas de dos b y un a (abb, bab y bba).

Obviamente, sólo hay una palabra de tres letras constituidas de a solamente, y esto corresponde al monomio 1·a³, con 1 = ${3 \choose 0}$ ( «0 » por ninguna b).

En vez de hablar de palabras formadas con a y b, es equivalente imaginar una hilera de n cajones inicialmente vacíos, y p bolas intercambiables que se tienen que repartir, en cada cajón no cabiendo más de una. Se trata en todos casos de repartir p objetos entre n sitios posibles, o de escoger un grupo de p objetos/sitios entre n objetos/sitios. De ahí la apelación p entre n.

Todo lo anterior lleva al teorema:

Hay exactamente

${n \choose p}$

maneras de escoger un conjunto de p elementos entre n elementos.

En matemática formal, se prefiere hablar de conjuntos:

Existen

${n \choose p}$

subconjuntos de cardenal p en un conjunto de cardenal n.

Este punto de vista permite hallar la fórmula para los coeficientes binomiales. En efecto, para elegir el « primer » elemento, hay n posibilidades, luego para escoger el segundo quedan n-1 posibilidades y así sucesivamente hasta el element número p, que tiene n-p+1. El orden en el que se ha elegido estos p elementos no importa, se podía haber obtenido el mismo subconjunto de p elementos en otro orden. Hay p! permutaciones posibles de estos p elementos, es decir p! maneras de obtener el mismo conjunto.

Por tanto hay

${\frac {n\cdot (n-1)\cdot (n-2)...(n-p+1)}{p!}}$

subconjuntos posibles.

En conclusión:

${n \choose p}={\frac {n\cdot (n-1)\cdot (n-2)...(n-p+1)}{p\cdot (p-1)\cdot (p-2)...2\cdot 1}}={\frac {n!}{p!\cdot (n-p)!}}$

Verifiquémoslo en un ejemplo:

${5 \choose 2}={\frac {5!}{2!3!}}={\frac {5\times 4\times 3\times 2}{2\times 3\times 2}}=10$

En el triángulo, el valor en la quinta línea y segunda columna es 10. Para rematar, listemos las palabras de cinco letras formadas de 2 a y 5-2 = 3 b (en el orden alfabético, o en el orden creciente considerando que a es la cifra 0 y b la cifra 1):
aabbb, ababb, abbab, abbba, baabb, babab, babba,bbaab, bbaba, bbbaa.

La fórmula permite verificar todas las propiedades del párrafo anterior, sin embargo se puede prescindir de los cálculos en la mayoría de los casos, con tal de manipular los conceptos idoneos.

Un subconjunto A de E define una partición de E en dos partes E = A ∪ B , con A ∩ B = {}= ∅ (conjunto vacío). Aquí $B={\overline {A}}$ es el complementario de A en E.

Da lo mismo escoger los p elementos de A que los n-p elementos de ${\overline {A}}$.

Esto justifica, sin cálculo, la simetría

${n \choose {n-p}}={n \choose p}$.

Si p > n, no hay subconjuntos de E con p elementos, porque E contiene sólo n, luego

${n \choose p}=0$

También son evidentes las igualdades

${n \choose 1}=n$

y

${n \choose 0}=1$

porque, en el primer caso,

hay tantas maneras de escoger subconjunto de tamaño 1 que de elementos de E, y en el segundo caso, sólo existe un conjunto con cero elemento: el conjunto vacío.

La regla fundamental también tiene explicación gráfica:

Prueba: se escoge un elemento e cualquiera de E, que contiene n+1 elementos: E = E' ∪ {e}. Luego se consideran los subconjuntos A de E de cardenal p+1. Son de dos tipos: o contienen e, o no.

Si e ∈ A, entonces falta elegir p elementos de E' para completar A. Hay

${n \choose p}$

posibilidades.

Si e ∉ A, entonces falta elegir p+1 elementos de E' para definir A. Hay

${n \choose {p+1}}$

posibilidades.

Sumando los dos casos, se obtiene todos las partes de p+1 elementos de E, constituido de n+1 elementos.

Hay por tanto

${{n+1} \choose {p+1}}={n \choose {p+1}}+{n \choose p}$

Un ejemplo:

Aquí va una propiedad aritmética, sin interpretación geométrica: cuando n es primo, los coeficientes binomiales en la línea n son divisibles por n, excepto los dos bordes de la misma (que valen 1). Escrito formalmente:

Teorema :

$\forall p\in [1;n-1],n/{n \choose p}$

En la figura, los ejemplos están en verde, y los contraejemplos (cuando n no es primo y p divide n) en amarillo.

Prueba: en la fracción

${\frac {n!}{p!(n-p)!}}$

el factor primo

n aparece una vez en el numerador y jamás en el denomininador. (El denominador es un producto de números entre 1 y n-1). Por tanto la fracción es divisible por n.

V Generalización

En vez de considerar las potencias de a + b, se puede mirar las del trinomio a + b + c.
(a + b + c)ⁿ es una suma de monomios de la forma λ_p,q,r ·a^p·b^q·c^r, con p, q y r positivos, p + q + r = n, y λ_p,q,r un natural que se tendría que llamar coeficiente trinomial.

Los cálculos son similares a los del coeficiente binomial, y dan la expresión siguiente:

$\lambda _{p,q,r}={\frac {n!}{p!q!r!}}$

Corresponde al número de partición en tres de un conjunto de n elementos, en subconjuntos de p, q y r elementos. Un ejemplo:

Estos coeficientes se pueden hallar en la analogía tridimensional del triángulo de Pascal: Se podría llamar la pirámide de Pascal, es también infinita, con secciones triangulares, y el valor en cada casilla es la suma de los valores de las tres casillas encima de ella.
Se ha dibujado las primeras secciones a partir de la cumbre.
Se observa una invariance por rotación de 120 grados alrededor de un eje vertical que pasa por el vértice.
El triángulo de Pascal aparece en las tres caras de la pirámide.

Está claro que todo esto se puede generalizar a dimensiones finitas cualquieras, pero sin la posibilidad de hacer dibujitos explicativos.

Autor: M.Romero Schmidtke