Teoría de la plasticidad

La teoría de la plasticidad es una rama de la mecánica de sólidos deformables que se utiliza para describir el comportamiento de los materiales que conservan remanentemente deformaciones impuestas. Se caracteriza por el supuesto de que existe una regla de flujo[1] que puede usarse para determinar la cantidad de deformación plástica en el material.
En consecuencia, se supone que la deformación total de un cuerpo se puede descomponer de forma aditiva (o multiplicativa) en una parte elástica y una parte plástica. La parte elástica de la deformación se puede calcular a partir de un modelo constitutivo elástico lineal o hiperelástico. Sin embargo, la determinación de la parte plástica de la deformación requiere una regla de flujo y un modelo de endurecimiento.
Teoría de la pequeña deformación[editar]
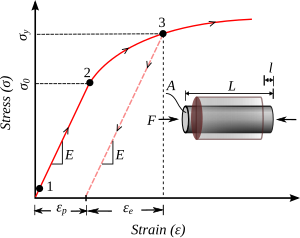
Las teorías típicas de plasticidad de flujo para cargas unidireccionales (para plasticidad perfecta de deformación pequeña o plasticidad de endurecimiento) se desarrollan sobre la base de los siguientes requisitos:
- El material tiene un rango elástico lineal.
- El material tiene un límite elástico definido como la tensión a la que se produce por primera vez la deformación plástica, es decir, .
- Más allá del límite elástico, el estado de tensión siempre permanece en la superficie de fluencia, es decir, .
- La carga se define como la situación en la que los incrementos de tensión son mayores que cero, es decir, . Si la carga lleva el estado de tensión al dominio plástico, entonces el incremento de la deformación plástica es siempre mayor que cero, es decir, .
- La descarga se define como la situación en la que los incrementos de tensión son menores que cero, es decir, . El material es elástico durante la descarga y no se acumula ninguna tensión plástica adicional.
- La deformación total es una combinación lineal de las partes elástica y plástica, es decir, . La parte plástica no se puede recuperar mientras que la parte elástica sea totalmente recuperable.
- El trabajo realizado de un ciclo de carga-descarga es positivo o cero, es decir, . Esto también se denomina postulado de estabilidad de Drucker, y elimina la posibilidad de un comportamiento de ablandamiento de las deformaciones.
Los requisitos anteriores se pueden expresar en estados tridimensionales de tensión y carga multidireccional de la siguiente manera:
- Elasticidad (ley de elasticidad de Hooke). En el régimen elástico lineal, las tensiones y deformaciones en el material están relacionadas por
- donde la matriz de rigidez es constante.
- Límite elástico (superficie de fluencia). El límite elástico está definido por una superficie de fluencia que no depende de la deformación plástica y tiene la forma
- Más allá del límite elástico. Para materiales endurecibles por deformación, la superficie de fluencia evoluciona al aumentar la deformación plástica y el límite elástico cambia. La superficie de rendimiento evolutiva tiene la forma
- Carga. Para estados generales de tensión, la carga plástica se indica si el estado de tensión está en la superficie de fluencia y el incremento de tensión se dirige hacia el exterior de la superficie de fluencia; Esto ocurre si el producto interno del incremento de tensión y la normal exterior de la superficie de fluencia es positivo, es decir,
- La ecuación anterior, cuando es igual a cero, indica un estado de carga neutra donde el estado de tensión se mueve en la superficie de fluencia.
- Descarga: Se hace un argumento similar para la descarga, para cuya situación , el material está en el dominio elástico, y
- Descomposición de la deformación: La descomposición aditiva de la deformación en partes elásticas y plásticas se puede escribir como
- Postulado de estabilidad: El postulado de estabilidad se expresa como
Regla de flujo[editar]
En plasticidad de metales, la suposición de que el incremento de deformación plástica y el tensor de tensión desviatoria tienen las mismas direcciones principales se resume en una relación llamada regla de flujo. Las teorías de la plasticidad de las rocas también utilizan un concepto similar, excepto que el requisito de dependencia de la presión de la superficie de fluencia requiere una relajación del supuesto anterior. En cambio, normalmente se supone que el incremento de la deformación plástica y la normal a la superficie de fluencia dependiente de la presión tienen la misma dirección, es decir,
donde es un parámetro de endurecimiento. Esta forma de regla de flujo se denomina regla de flujo asociada y el supuesto de codireccionalidad se denomina condición de normalidad. La función también se llama potencial plástico.
La regla de flujo anterior se justifica fácilmente para deformaciones perfectamente plásticas para las que cuando , es decir, la superficie de fluencia permanece constante bajo una deformación plástica creciente. Esto implica que el incremento de la deformación elástica también es cero, , debido a la ley de Hooke. Por lo tanto,
Por lo tanto, tanto la normal a la superficie de fluencia como el tensor de deformación plástica son perpendiculares al tensor de tensión y deben tener la misma dirección.
Para un material endurecido mecánicamente, la superficie de fluencia puede expandirse al aumentar la tensión. Se asume el segundo postulado de estabilidad de Drucker, que establece que para un ciclo de tensión infinitesimal este trabajo plástico es positivo, es decir,
La cantidad anterior es igual a cero para ciclos puramente elásticos. El examen del trabajo realizado durante un ciclo de carga y descarga plástico puede utilizarse para justificar la validez de la regla de flujo asociada.[2]
Condición de consistencia[editar]
La condición de consistencia de Prager es necesaria para cerrar el conjunto de ecuaciones constitutivas y eliminar el parámetro desconocido del sistema de ecuaciones. La condición de consistencia establece que , dado que , y por lo tanto
Teoría de grandes deformaciones[editar]
Las teorías de la plasticidad sobre el flujo con grandes deformaciones suelen comenzar con uno de los siguientes supuestos:
- El tensor de la tasa de deformación se puede descomponer de forma aditiva en una parte elástica y en una parte plástica, o
- El tensor del gradiente de deformación se puede descomponer multiplicativamente en una parte elástica y en una parte plástica.
El primer supuesto se utilizó ampliamente para simulaciones numéricas del comportamiento de los metales, pero gradualmente ha sido reemplazado por la teoría multiplicativa.
Cinemática de la plasticidad multiplicativa[editar]
El concepto de descomposición multiplicativa del gradiente de deformación en partes elásticas y plásticas fue propuesto por primera vez de forma independiente por B. A. Bilby,[3] E. Kröner,[4] en el contexto de la plasticidad de cristales y extendido a la plasticidad continua por Erasmus Lee.[5] La descomposición supone que el gradiente de deformación total (F) se puede descomponer como:
donde Fe es la parte elástica (recuperable) y Fp es la parte plástica (irrecuperable) de la deformación. El gradiente de velocidad espacial viene dado por
donde un punto superpuesto indica una derivada respecto al tiempo. Se puede escribir lo anterior como
La cantidad
se denomina gradiente de velocidad plástica y se define en una configuración libre de tensiones intermedia (incompatible). La parte simétrica (Dp) de Lp se denomina tasa de deformación plástica, mientras que la parte antisimétrica (Wp) se llama giro plástico:
Normalmente, el giro plástico se ignora en la mayoría de las descripciones de plasticidad finita.
Régimen elástico[editar]
El comportamiento elástico en el régimen de deformaciones finitas normalmente se describe mediante un modelo hiperelástico. La deformación elástica se puede medir utilizando un tensor de deformación de Cauchy-Green elástico derecho definido como:
El tensor logarítmico o de deformación de Hencky puede definirse entonces como
El tensor de tensión de Mandel simetrizado es una medida de tensión conveniente para la plasticidad finita y se define como
donde S es el segunda tensión de Piola-Kirchhoff. Un posible modelo hiperelástico en términos de deformación logarítmica es[6]
donde W es una función de densidad de energía de deformación, J = det(F), μ es un módulo y dev indica la parte desviadora de un tensor.
Regla de flujo[editar]
La aplicación de la desigualdad de Clausius-Duhem conduce, en ausencia de un giro plástico, a la regla del flujo de la deformación finita
Condiciones de carga-descarga[editar]
Se puede demostrar que las condiciones de carga y descarga son equivalentes a las condiciones de Karush-Kuhn-Tucker.
Condición de consistencia[editar]
La condición de consistencia es idéntica a la del caso de deformaciones pequeñas,
Referencias[editar]
- ↑ Lubliner, Jacob (2008), Plasticity Theory, Courier Dover Publications..
- ↑ Anandarajah (2010).
- ↑ Bilby, B. A.; Bullough, R.; Smith, E. (1955), «Continuous distributions of dislocations: a new application of the methods of non-Riemannian geometry», Proceedings of the Royal Society 231 (1185): 263-273, Bibcode:1955RSPSA.231..263B, doi:10.1098/rspa.1955.0171.
- ↑ Kröner, E. (1958), «Kontinuumstheorie der Versetzungen und Eigenspannungen», Erg. Angew. Math. 5: 1-179.
- ↑ Lee, E. H. (1969), «Elastic-Plastic Deformation at Finite Strains», Journal of Applied Mechanics 36 (1): 1-6, Bibcode:1969JAM....36....1L, doi:10.1115/1.3564580.Uso incorrecto de la plantilla enlace roto (enlace roto disponible en Internet Archive; véase el historial, la primera versión y la última).
- ↑ Anand, L. (1979), «On H. Hencky's approximate strain-energy function for moderate deformations», Journal of Applied Mechanics 46 (1): 78-82, Bibcode:1979JAM....46...78A, doi:10.1115/1.3424532.


































![{\displaystyle {\begin{aligned}{\boldsymbol {l}}&={\dot {\boldsymbol {F}}}\cdot {\boldsymbol {F}}^{-1}=\left({\dot {\boldsymbol {F}}}^{e}\cdot {\boldsymbol {F}}^{p}+{\boldsymbol {F}}^{e}\cdot {\dot {\boldsymbol {F}}}^{p}\right)\cdot \left[({\boldsymbol {F}}^{p})^{-1}\cdot ({\boldsymbol {F}}^{e})^{-1}\right]\\&={\dot {\boldsymbol {F}}}^{e}\cdot ({\boldsymbol {F}}^{e})^{-1}+{\boldsymbol {F}}^{e}\cdot [{\dot {\boldsymbol {F}}}^{p}\cdot ({\boldsymbol {F}}^{p})^{-1}]\cdot ({\boldsymbol {F}}^{e})^{-1}\,.\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/755b7a810c84c898594fd30e20070f3168f37c68)


![{\displaystyle {\boldsymbol {D}}^{p}={\tfrac {1}{2}}[{\boldsymbol {L}}^{p}+({\boldsymbol {L}}^{p})^{T}]~,~~{\boldsymbol {W}}^{p}={\tfrac {1}{2}}[{\boldsymbol {L}}^{p}-({\boldsymbol {L}}^{p})^{T}]\,.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/88b277fc84b2032ba6be43bacc0dcc2cf50e31e5)






