Teoría de cantidad de movimiento
La teoría de la cantidad de movimiento o Teoría de Froude es, en mecánica de fluidos, una formulación matemática de la física de hélices basada en la variación de cantidad de movimiento. Fue elaborada en el siglo XIX por William John Macquorn Rankine y Robert Edmund Froude (1889). Esta teoría se aplica a los rotores de helicópteros, a las hélices de navíos y de aeronaves, a los aerogeneradores e hidrogeneradores. Supone una buena aproximación inicial al comportamiento aerodinámico del rotor del helicóptero, aunque necesita ser mejorada.
Teoría de la cantidad de movimiento para vuelo axial[editar]
La teoría de Froude considera la hélice como un disco uniforme. El disco de la hélice aparece como una hélice que posee una infinidad de paletas de espesor infinitamente pequeño.
Las hipótesis a partir de las que se aplica esta teoría son:
- En vuelo axial, el movimiento es unidimensional.
- El movimiento es casi estacionario, se pueden despreciar las variables temporales.
- Fluido incompresible.
- Fluido no viscoso.
- La estela del rotor no tiene movimiento de rotación, únicamente vertical.
- La velocidad inducida es uniforme en todo el plano del rotor.
- Sobre el fluido no se aplica ninguna fuerza externa.
- Las ecuaciones se plantean en ejes ligados al rotor.
Para aplicar estas ecuaciones se toma como volumen de control el de la figura 1.1. El volumen de control empieza en el infinito aguas arriba, y se extiende en la dirección positiva, hacia abajo. El fluido se acelera a medida que se acerca al disco rotor.
Salto de presiones en el rotor[editar]
Estados de operación del rotor[editar]
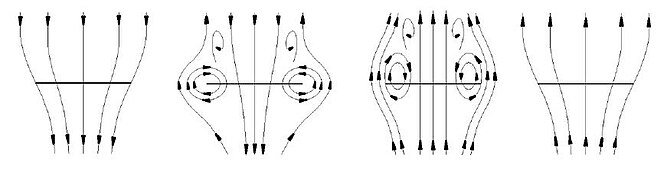
El flujo a través del rotor y en sus inmediaciones se comporta de forma diferente según la velocidad vertical del helicóptero. En algunos casos no es posible aplicar la teoría de la cantidad de movimiento y es necesario recurrir a soluciones experimentales. Se distinguen principalmente cuatro estados de operación del rotor.
- Operación normal
En vuelo ascensional y hasta el límite de vuelo a punto fijo ( ) el flujo en el rotor es altamente periódico. Los vórtices de punta de pala están libres de perturbaciones, y siguen trayectorias helicoidales suaves y bien definidas.
Para vuelo vertical descendente (poca o nula velocidad horizontal) motorizado a velocidad de descenso relativamente baja (superior no obstante al 75% de Vf, siendo Vf la velocidad inducida del flujo en régimen estacionario). Si la velocidad de descenso es inferior a la citada no se produce tal perturbación. La alta potencia del rotor y el descenso relativamente elevado provocan que la aeronave se sitúe dentro de su propia turbulencia. Los vórtices de punta de pala se desplazan hacia el plano del rotor y hacia el exterior de las palas, generando una situación no estacionaria y aperiódica, donde se acumulan los vórtices formando una serie de anillos. No es posible distinguir una superficie que defina la estela, lo que impide aplicar la teoría de la cantidad de movimiento. Además en estas condiciones aumentan las vibraciones y se dificulta el pilotaje. Para corregir esta situación es necesario aumentar la velocidad horizontal (desplazamiento del bastón de mando cíclico) y reducir el paso del mando colectivo (intensidad de la turbulencia).
Para velocidades de descenso medias, del orden de la estela se vuelve aún más turbulenta, y el flujo es similar al de un cuerpo no aerodinámico. Tampoco se puede identificar la estela, de forma que tampoco se puede aplicar en este caso la teoría de la cantidad de movimiento.
Si la velocidad de descenso es elevada ( ) la estela vuelve a estar definida, y la teoría de la cantidad de movimiento se puede volver a aplicar. En esta situación el rotor extrae energía del flujo.
Hipótesis[editar]
La teoría de Froude considera la hélice como un disco uniforme. El disco de la hélice aparece como una hélice que posee una infinidad de paletas de espesor infinitamente pequeño.
Las hipótesis de la teoría de Froude son las siguientes:
- El fluido es irrotacional
- El fluido es incompresible
- El disco de la hélice no provoca un vórtice de estela helicoidal
- El flujo es estrictamente axial y uniforme sobre toda la superficie del disco de la hélice así como en toda la sección del fluido. El flujo por lo tanto, es unidireccional.
- Las fuerzas de fricción son despreciables.
Se considera que el disco de la hélice se desplaza de forma uniforme y rectilínea en el fluido de velocidad V al infinito. El efecto principal del disco de la hélice es la aceleración del fluido a su paso. Esta aceleración se acompaña de una discontinuidad de presión y de una contracción de la sección transversal. En efecto, el disco de la hélice ejerce una fuerza de empuje T (en inglés: thrust) sobre el fluido por la variación de su cantidad de movimiento.
En la figura se observa una velocidad V al infinito. Esta velocidad es algebraica, lo que significa que puede ser positiva (en caso de que las hélices del rotor del helicóptero en vuelo vertical ascienda), nula (rotor del helicóptero en vuelo estacionario) o negativa (en el caso de aerogeneradores y rotor del helicóptero en vuelo vertical descendiente). En ese orden serán estudiados los casos respectivamente.
Vuelo estacionario[editar]

La velocidad al paso por el disco de la hélice es llamada velocidad inducida. Ella produce la velocidad al infinito posterior. La ecuación de continuidad del fluido se escribe:
El empuje está dado por la variación de la cantidad de movimiento:
El empuje puede igualmente estar expresada en función de la discontinuidad de presión:
Escribimos la relación de Bernoulli antes y después del disco de la hélice :
La relación siguiente es deducida:
| Demostracion: |
|---|
| Teorema de Bernoulli :
Consideramos que no hay variación de altitud, por lo tanto:
Obtenemos por lo tanto que antes y después del disco de la hélice:
Sustituyendo,
Reducimos a:
Ahora bien, sabemos que el empuje puede estar descrito por la variación de la presión o por la variación de velocidad:
Obtenemos:
Por lo tanto:
Simplificamos:
La expression del empuje dado por la variación de la cantidad de movimiento puede ser simplificada:
|
Así, la velocidad de la estela al infinito posterior es el doble de la velocidad inducida. Tenemos la relación:
De esta forma, la velocidad inducida varía con la carga superficial del dico de la hélice: . La potencia necesaria para la aceleración del fluido está dada por la expresión:
Esta potencia es llamada potencia inducida. Observaros con facilidad que la potencia inducida varía con la velocidad inducida y con la carga superficial del disco de la hélice. Conviene notar que la potencia inducida por el vuelo estacionario constituye la potencia requerida esencial para el vuelo de un helicóptero. Por lo tanto aparece claramente la importancia del dimensionamiento de un rotor.
Coeficientes adimensionales[editar]
Con el fin de efectuar comparaciones pertinentes entre hélices diferentes, conviene definir coeficientes adimensionales. En lo que concierne la velocidad, la referencia está constituida por la velocidad al extremo de la aspa:
La hipótesis de incompresibilidad corresponde al límite del dominio subsónico para la velocidad al extremo del aspa. Los coeficientes de velocidad inducida se escriben:
Para el empuje, consideramos una sustentación uniforme del disco de la hélice:
où
Remarcaremos la presencia de un coeficiente en el denominador. Su empleo no esta generalizado. En consecuencia, se debe tener cuidado de consultar la definición del coeficiente de empuje antes de cualquier comparación. Cualquier omisión en esta área puede resultar muy molesta.
Obtenemos las relaciones:
Un coeficiente de potencia inducida está definido:
Tenemos las relaciones siguientes:
Vuelo ascendente[editar]
La ecuación de conservación de flujo se escribe:
La variación de la cantidad de movimiento dada por el empuje:
Escribimos la relación de Bernulli antes y después de la hélice del disco:
Deducimos la relación:
| Demostración : |
|---|
| Obtenemos con el teorema de Benoulli antes y después del disco de la hélice:
Sustituyendo,
Reducimos:
Desarrollamos:
Así, sabemos que el empuje puede ser dado por la variación de presión o por la variación de velocidad:
Obtenemos :
Donde:
Simplificamos:
|
Notamos que esa relación es la misma que en el caso del vuelo estacionario. Remplazando en la expresión del empuje, da:
Notando la velocidad inducida dando el mismo empuje que en vuelo estacionario, calculamos:
En coeficientes adimensionales, estableciendo como coeficiente de velocidad, obtenemos:
Noción de eficiencia propulsora[editar]
En el caso de un avión, la potencia útil es:
La potencia desarrollada a tal efecto viene dada por el aumento de la energía cinética del fluido, es decir, la potencia inducida:
La eficiencia propulsora está definida por:
La consecuencia es que a igual empuje, la máxima eficiencia se obtendrá cuando la aceleración del aire sea mínima, es decir el caudal máximo. En otras palabras, cuanto mayor sea el diámetro de la hélice, mayor será la eficiencia del propulsor.
Vuelo descendente[editar]

La ecuación de la conservación del flujo se escribe:
La variación de la cantidad de movimiento donde el empuje:
Escibimos la relación de Bernoulli antes y después del disco de la hélice:
Deducimos la relación:
| Demostración: |
|---|
| Obtenemos con el teorema de Bernoulli antes y después del disco de la hélice:
Sustituyendo,
Desarrollamos:
Así, sabemos que el empuje puede ser dado por la variación de la presión o por la variación de la velocidad:
Obtenemos:
Por lo tanto:
Simplificamos:
|
Notamos que esa relación es la misma que en el caso del vuelo estacionario y del vuelo ascendente. Remplazando en la expresión del empuje, da:
En vista de esos resultados, parece que el vuelo descendente no presenta una dificultad particular en la medida en la que las relaciones son similares a las del vuelo ascendente. Esa similitud aparente es engañosa: en efecto, comparemos las dos expresiones del empuje:
En vuelo estacionario, tenemos:

Si nosotros remplazamos esas expresiones en aquella del empuje en el vuelo descendente, obtenemos:
Esto no es apropiado ya que el impulso es siempre positivo y hacia arriba. Por tanto, y a diferencia del caso del vuelo ascendente, la expresión del empuje en el vuelo descendente no puede extenderse al caso del vuelo estacionario. Por tanto, hay un dominio por definir en el que la teoría de Froude no es adecuada para modelar un vuelo descendente.
Consideremos una velocidad algebraica (positiva en vuelo ascendente y negativa en vuelo descendente). Introducimos las velocidades adimensionales:
Obtenemos las relaciones:

Soit :
La teoría de Froude supone un flujo uniaxial. Así, aproximado al valor:
Parece que se puede producir una inversión del sentido del flujo localmente. En consecuencia, el intervalo comprendido entre y debe ser retirado del dominio de validez de las fórmulas obtenidas:
Adimensionalización de las ecuaciones[editar]
Véase también[editar]
Bibliografía[editar]
- Diseño de helicópteros y aeronaves diversas. 4º curso de Ingeniería Aeronáutica. Septiembre de 2011. Escuela Técnica Superior de Ingeniería Industrial y Aeronáutica de Tarrasa, de la Universidad Politécnica de Cataluña (ETSEIAT – UPC).
- Ingeniería Aeroespacial,Helicópteros, Open Course Ware, UPM
- (en inglés) — PDF Momentum theory (Froude) Archivado el 21 de octubre de 2016 en Wayback Machine.
































































